Proximally Guided Stochastic Subgradient Method for Nonsmooth, Nonconvex Problems
Paper and Code
Sep 18, 2018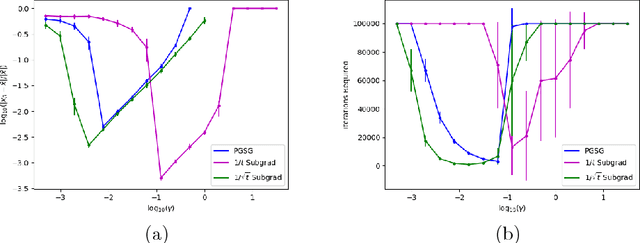
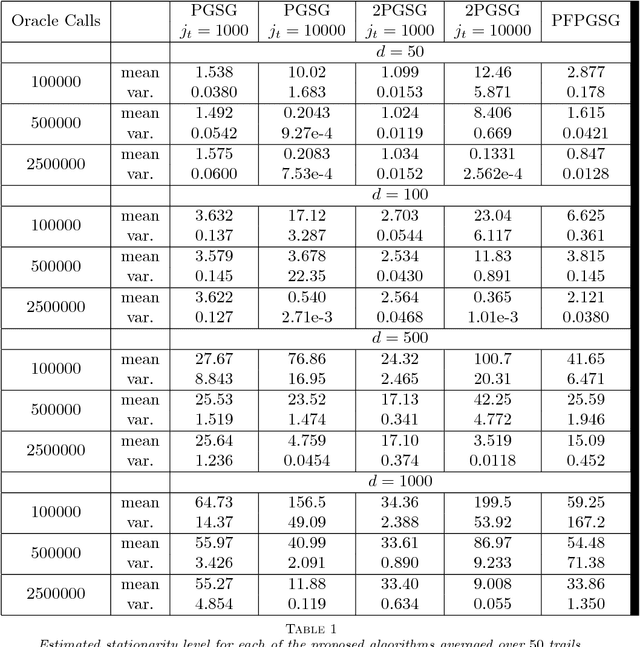
In this paper, we introduce a stochastic projected subgradient method for weakly convex (i.e., uniformly prox-regular) nonsmooth, nonconvex functions---a wide class of functions which includes the additive and convex composite classes. At a high-level, the method is an inexact proximal point iteration in which the strongly convex proximal subproblems are quickly solved with a specialized stochastic projected subgradient method. The primary contribution of this paper is a simple proof that the proposed algorithm converges at the same rate as the stochastic gradient method for smooth nonconvex problems. This result appears to be the first convergence rate analysis of a stochastic (or even deterministic) subgradient method for the class of weakly convex functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge