Bundle Method Sketching for Low Rank Semidefinite Programming
Paper and Code
Nov 11, 2019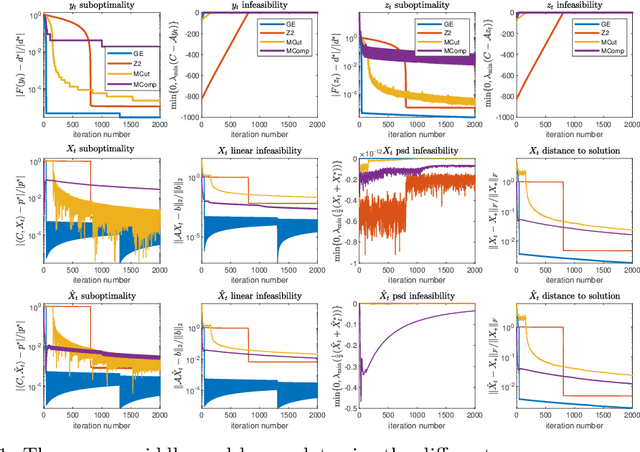
In this paper, we show that the bundle method can be applied to solve semidefinite programming problems with a low rank solution without ever constructing a full matrix. To accomplish this, we use recent results from randomly sketching matrix optimization problems and from the analysis of bundle methods. Under strong duality and strict complementarity of SDP, we achieve $\tilde{O}(\frac{1}{\epsilon})$ convergence rates for both the primal and the dual sequences, and the algorithm proposed outputs a $O(\sqrt{\epsilon})$ approximate solution $\hat{X}$ (measured by distances) with a low rank representation with at most $\tilde{O}(\frac{1}{\epsilon})$ many iterations.
* 8 pages, 1 figure
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge