How Over-Parameterization Slows Down Gradient Descent in Matrix Sensing: The Curses of Symmetry and Initialization

This paper rigorously shows how over-parameterization changes the convergence behaviors of gradient descent (GD) for the matrix sensing problem, where the goal is to recover an unknown low-rank ground-truth matrix from near-isotropic linear measurements. First, we consider the symmetric setting with the symmetric parameterization where $M^* \in \mathbb{R}^{n \times n}$ is a positive semi-definite unknown matrix of rank $r \ll n$, and one uses a symmetric parameterization $XX^\top$ to learn $M^*$. Here $X \in \mathbb{R}^{n \times k}$ with $k > r$ is the factor matrix. We give a novel $\Omega (1/T^2)$ lower bound of randomly initialized GD for the over-parameterized case ($k >r$) where $T$ is the number of iterations. This is in stark contrast to the exact-parameterization scenario ($k=r$) where the convergence rate is $\exp (-\Omega (T))$. Next, we study asymmetric setting where $M^* \in \mathbb{R}^{n_1 \times n_2}$ is the unknown matrix of rank $r \ll \min\{n_1,n_2\}$, and one uses an asymmetric parameterization $FG^\top$ to learn $M^*$ where $F \in \mathbb{R}^{n_1 \times k}$ and $G \in \mathbb{R}^{n_2 \times k}$. Building on prior work, we give a global exact convergence result of randomly initialized GD for the exact-parameterization case ($k=r$) with an $\exp (-\Omega(T))$ rate. Furthermore, we give the first global exact convergence result for the over-parameterization case ($k>r$) with an $\exp(-\Omega(\alpha^2 T))$ rate where $\alpha$ is the initialization scale. This linear convergence result in the over-parameterization case is especially significant because one can apply the asymmetric parameterization to the symmetric setting to speed up from $\Omega (1/T^2)$ to linear convergence. On the other hand, we propose a novel method that only modifies one step of GD and obtains a convergence rate independent of $\alpha$, recovering the rate in the exact-parameterization case.

Provably Convergent Policy Optimization via Metric-aware Trust Region Methods

Trust-region methods based on Kullback-Leibler divergence are pervasively used to stabilize policy optimization in reinforcement learning. In this paper, we exploit more flexible metrics and examine two natural extensions of policy optimization with Wasserstein and Sinkhorn trust regions, namely Wasserstein policy optimization (WPO) and Sinkhorn policy optimization (SPO). Instead of restricting the policy to a parametric distribution class, we directly optimize the policy distribution and derive their closed-form policy updates based on the Lagrangian duality. Theoretically, we show that WPO guarantees a monotonic performance improvement, and SPO provably converges to WPO as the entropic regularizer diminishes. Moreover, we prove that with a decaying Lagrangian multiplier to the trust region constraint, both methods converge to global optimality. Experiments across tabular domains, robotic locomotion, and continuous control tasks further demonstrate the performance improvement of both approaches, more robustness of WPO to sample insufficiency, and faster convergence of SPO, over state-of-art policy gradient methods.

A Validation Approach to Over-parameterized Matrix and Image Recovery

In this paper, we study the problem of recovering a low-rank matrix from a number of noisy random linear measurements. We consider the setting where the rank of the ground-truth matrix is unknown a prior and use an overspecified factored representation of the matrix variable, where the global optimal solutions overfit and do not correspond to the underlying ground-truth. We then solve the associated nonconvex problem using gradient descent with small random initialization. We show that as long as the measurement operators satisfy the restricted isometry property (RIP) with its rank parameter scaling with the rank of ground-truth matrix rather than scaling with the overspecified matrix variable, gradient descent iterations are on a particular trajectory towards the ground-truth matrix and achieve nearly information-theoretically optimal recovery when stop appropriately. We then propose an efficient early stopping strategy based on the common hold-out method and show that it detects nearly optimal estimator provably. Moreover, experiments show that the proposed validation approach can also be efficiently used for image restoration with deep image prior which over-parameterizes an image with a deep network.

Flat minima generalize for low-rank matrix recovery

Empirical evidence suggests that for a variety of overparameterized nonlinear models, most notably in neural network training, the growth of the loss around a minimizer strongly impacts its performance. Flat minima -- those around which the loss grows slowly -- appear to generalize well. This work takes a step towards understanding this phenomenon by focusing on the simplest class of overparameterized nonlinear models: those arising in low-rank matrix recovery. We analyze overparameterized matrix and bilinear sensing, robust PCA, covariance matrix estimation, and single hidden layer neural networks with quadratic activation functions. In all cases, we show that flat minima, measured by the trace of the Hessian, exactly recover the ground truth under standard statistical assumptions. For matrix completion, we establish weak recovery, although empirical evidence suggests exact recovery holds here as well. We complete the paper with synthetic experiments that illustrate our findings.

Algorithmic Regularization in Model-free Overparametrized Asymmetric Matrix Factorization

We study the asymmetric matrix factorization problem under a natural nonconvex formulation with arbitrary overparamatrization. We consider the model-free setting with no further assumption on the rank or singular values of the observed matrix, where the global optima provably overfit. We show that vanilla gradient descent with small random initialization and early stopping produces the best low-rank approximation of the observed matrix, without any additional regularization. We provide a sharp analysis on relationship between the iteration complexity, initialization size, stepsize and final error. In particular, our complexity bound is almost dimension-free and depends logarithmically on the final error, and our results have lenient requirements on the stepsize and initialization. Our bounds improve upon existing work and show good agreement with numerical experiments.

Rank Overspecified Robust Matrix Recovery: Subgradient Method and Exact Recovery

We study the robust recovery of a low-rank matrix from sparsely and grossly corrupted Gaussian measurements, with no prior knowledge on the intrinsic rank. We consider the robust matrix factorization approach. We employ a robust $\ell_1$ loss function and deal with the challenge of the unknown rank by using an overspecified factored representation of the matrix variable. We then solve the associated nonconvex nonsmooth problem using a subgradient method with diminishing stepsizes. We show that under a regularity condition on the sensing matrices and corruption, which we call restricted direction preserving property (RDPP), even with rank overspecified, the subgradient method converges to the exact low-rank solution at a sublinear rate. Moreover, our result is more general in the sense that it automatically speeds up to a linear rate once the factor rank matches the unknown rank. On the other hand, we show that the RDPP condition holds under generic settings, such as Gaussian measurements under independent or adversarial sparse corruptions, where the result could be of independent interest. Both the exact recovery and the convergence rate of the proposed subgradient method are numerically verified in the overspecified regime. Moreover, our experiment further shows that our particular design of diminishing stepsize effectively prevents overfitting for robust recovery under overparameterized models, such as robust matrix sensing and learning robust deep image prior. This regularization effect is worth further investigation.

TenIPS: Inverse Propensity Sampling for Tensor Completion

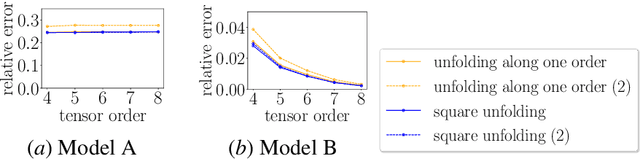
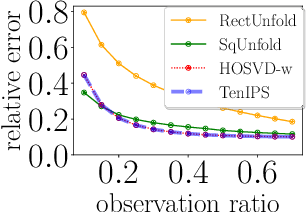
Tensors are widely used to represent multiway arrays of data. The recovery of missing entries in a tensor has been extensively studied, generally under the assumption that entries are missing completely at random (MCAR). However, in most practical settings, observations are missing not at random (MNAR): the probability that a given entry is observed (also called the propensity) may depend on other entries in the tensor or even on the value of the missing entry. In this paper, we study the problem of completing a partially observed tensor with MNAR observations, without prior information about the propensities. To complete the tensor, we assume that both the original tensor and the tensor of propensities have low multilinear rank. The algorithm first estimates the propensities using a convex relaxation and then predicts missing values using a higher-order SVD approach, reweighting the observed tensor by the inverse propensities. We provide finite-sample error bounds on the resulting complete tensor. Numerical experiments demonstrate the effectiveness of our approach.

Low-Rank Tensor Recovery with Euclidean-Norm-Induced Schatten-p Quasi-Norm Regularization

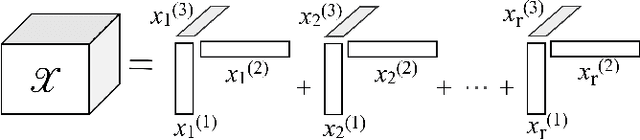
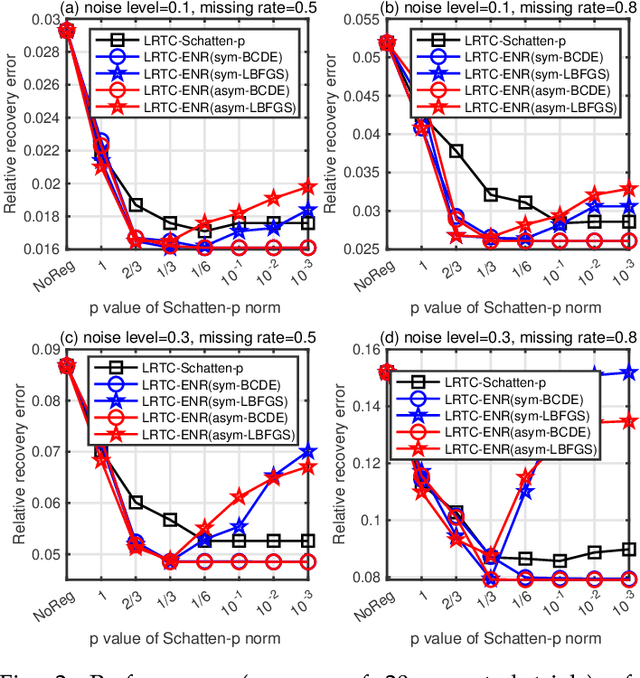
The nuclear norm and Schatten-$p$ quasi-norm of a matrix are popular rank proxies in low-rank matrix recovery. Unfortunately, computing the nuclear norm or Schatten-$p$ quasi-norm of a tensor is NP-hard, which is a pity for low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). In this paper, we propose a new class of rank regularizers based on the Euclidean norms of the CP component vectors of a tensor and show that these regularizers are monotonic transformations of tensor Schatten-$p$ quasi-norm. This connection enables us to minimize the Schatten-$p$ quasi-norm in LRTC and TRPCA implicitly. The methods do not use the singular value decomposition and hence scale to big tensors. Moreover, the methods are not sensitive to the choice of initial rank and provide an arbitrarily sharper rank proxy for low-rank tensor recovery compared to nuclear norm. We provide theoretical guarantees in terms of recovery error for LRTC and TRPCA, which show relatively smaller $p$ of Schatten-$p$ quasi-norm leads to tighter error bounds. Experiments using LRTC and TRPCA on synthetic data and natural images verify the effectiveness and superiority of our methods compared to baseline methods.

Low-rank matrix recovery with non-quadratic loss: projected gradient method and regularity projection oracle

Existing results for low-rank matrix recovery largely focus on quadratic loss, which enjoys favorable properties such as restricted strong convexity/smoothness (RSC/RSM) and well conditioning over all low rank matrices. However, many interesting problems involve non-quadratic loss do not satisfy such properties; examples including one-bit matrix sensing, one-bit matrix completion, and rank aggregation. For these problems, standard nonconvex approaches such as projected gradient with rank constraint alone (a.k.a. iterative hard thresholding) and Burer-Monteiro approach may perform badly in practice and have no satisfactory theory in guaranteeing global and efficient convergence. In this paper, we show that the critical component in low-rank recovery with non-quadratic loss is a regularity projection oracle, which restricts iterates to low-rank matrix within an appropriate bounded set, over which the loss function is well behaved and satisfies a set of relaxed RSC/RSM conditions. Accordingly, we analyze an (averaged) projected gradient method equipped with such an oracle, and prove that it converges globally and linearly. Our results apply to a wide range of non-quadratic problems including rank aggregation, one bit matrix sensing/completion, and more broadly generalized linear models with rank constraint.

$k$FW: A Frank-Wolfe style algorithm with stronger subproblem oracles

This paper proposes a new variant of Frank-Wolfe (FW), called $k$FW. Standard FW suffers from slow convergence: iterates often zig-zag as update directions oscillate around extreme points of the constraint set. The new variant, $k$FW, overcomes this problem by using two stronger subproblem oracles in each iteration. The first is a $k$ linear optimization oracle ($k$LOO) that computes the $k$ best update directions (rather than just one). The second is a $k$ direction search ($k$DS) that minimizes the objective over a constraint set represented by the $k$ best update directions and the previous iterate. When the problem solution admits a sparse representation, both oracles are easy to compute, and $k$FW converges quickly for smooth convex objectives and several interesting constraint sets: $k$FW achieves finite $\frac{4L_f^3D^4}{\gamma\delta^2}$ convergence on polytopes and group norm balls, and linear convergence on spectrahedra and nuclear norm balls. Numerical experiments validate the effectiveness of $k$FW and demonstrate an order-of-magnitude speedup over existing approaches.