Long-form factuality in large language models

Large language models (LLMs) often generate content that contains factual errors when responding to fact-seeking prompts on open-ended topics. To benchmark a model's long-form factuality in open domains, we first use GPT-4 to generate LongFact, a prompt set comprising thousands of questions spanning 38 topics. We then propose that LLM agents can be used as automated evaluators for long-form factuality through a method which we call Search-Augmented Factuality Evaluator (SAFE). SAFE utilizes an LLM to break down a long-form response into a set of individual facts and to evaluate the accuracy of each fact using a multi-step reasoning process comprising sending search queries to Google Search and determining whether a fact is supported by the search results. Furthermore, we propose extending F1 score as an aggregated metric for long-form factuality. To do so, we balance the percentage of supported facts in a response (precision) with the percentage of provided facts relative to a hyperparameter representing a user's preferred response length (recall). Empirically, we demonstrate that LLM agents can outperform crowdsourced human annotators - on a set of ~16k individual facts, SAFE agrees with crowdsourced human annotators 72% of the time, and on a random subset of 100 disagreement cases, SAFE wins 76% of the time. At the same time, SAFE is more than 20 times cheaper than human annotators. We also benchmark thirteen language models on LongFact across four model families (Gemini, GPT, Claude, and PaLM-2), finding that larger language models generally achieve better long-form factuality. LongFact, SAFE, and all experimental code are available at https://github.com/google-deepmind/long-form-factuality.

Large Language Models as Optimizers

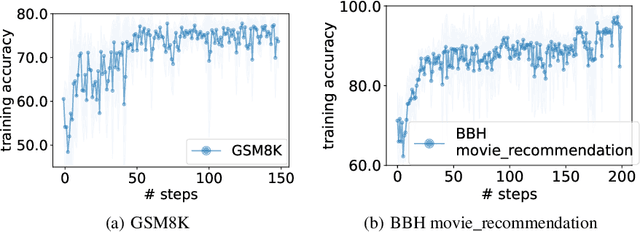
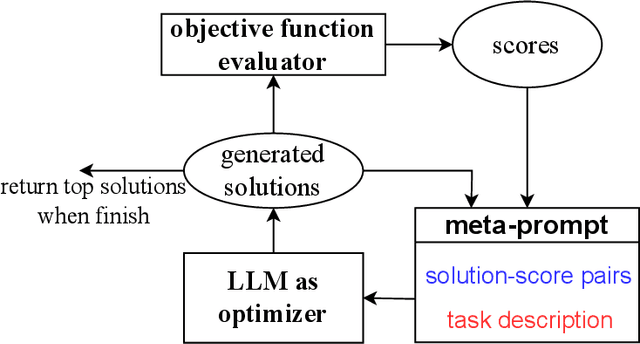
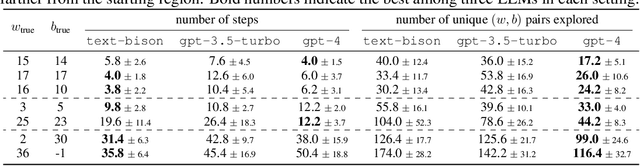
Optimization is ubiquitous. While derivative-based algorithms have been powerful tools for various problems, the absence of gradient imposes challenges on many real-world applications. In this work, we propose Optimization by PROmpting (OPRO), a simple and effective approach to leverage large language models (LLMs) as optimizers, where the optimization task is described in natural language. In each optimization step, the LLM generates new solutions from the prompt that contains previously generated solutions with their values, then the new solutions are evaluated and added to the prompt for the next optimization step. We first showcase OPRO on linear regression and traveling salesman problems, then move on to prompt optimization where the goal is to find instructions that maximize the task accuracy. With a variety of LLMs, we demonstrate that the best prompts optimized by OPRO outperform human-designed prompts by up to 8% on GSM8K, and by up to 50% on Big-Bench Hard tasks.

Resource-Constrained Neural Architecture Search on Tabular Datasets

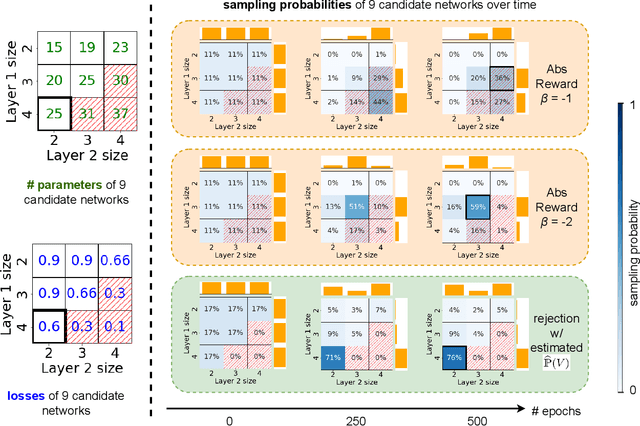
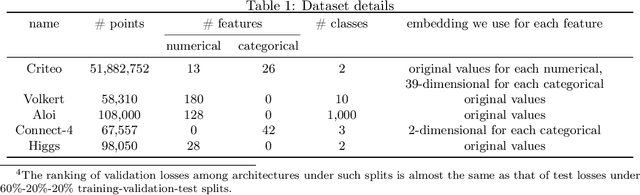
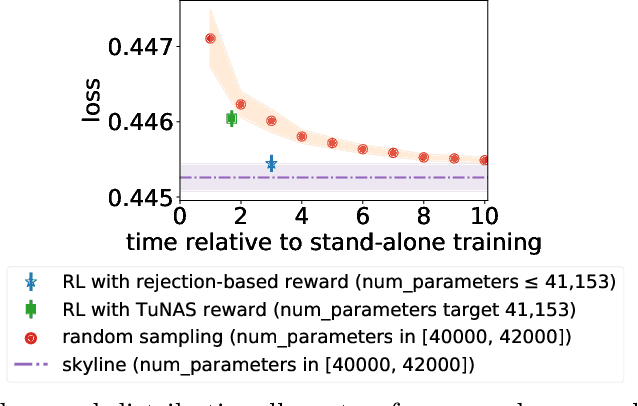
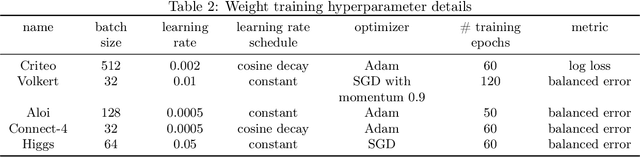
The best neural architecture for a given machine learning problem depends on many factors: not only the complexity and structure of the dataset, but also on resource constraints including latency, compute, energy consumption, etc. Neural architecture search (NAS) for tabular datasets is an important but under-explored problem. Previous NAS algorithms designed for image search spaces incorporate resource constraints directly into the reinforcement learning rewards. In this paper, we argue that search spaces for tabular NAS pose considerable challenges for these existing reward-shaping methods, and propose a new reinforcement learning (RL) controller to address these challenges. Motivated by rejection sampling, when we sample candidate architectures during a search, we immediately discard any architecture that violates our resource constraints. We use a Monte-Carlo-based correction to our RL policy gradient update to account for this extra filtering step. Results on several tabular datasets show TabNAS, the proposed approach, efficiently finds high-quality models that satisfy the given resource constraints.

How Low Can We Go: Trading Memory for Error in Low-Precision Training

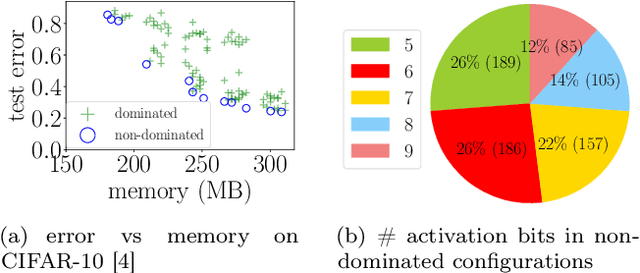
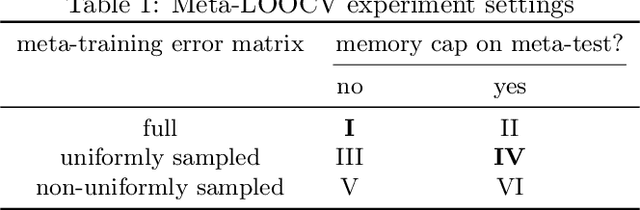
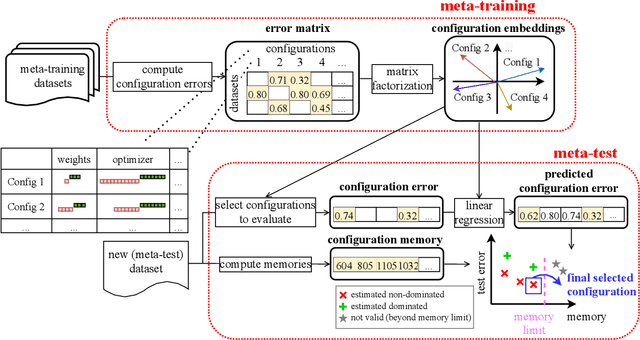
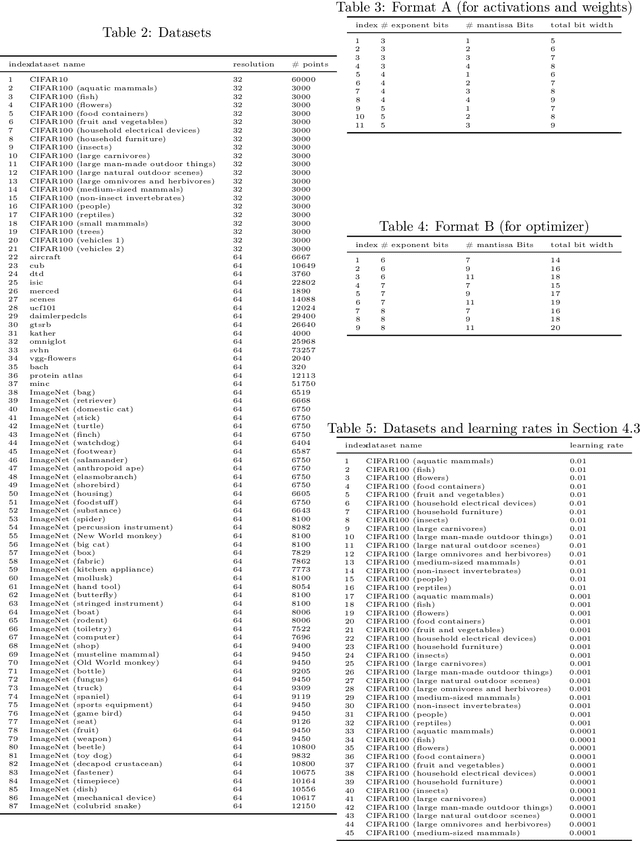
Low-precision arithmetic trains deep learning models using less energy, less memory and less time. However, we pay a price for the savings: lower precision may yield larger round-off error and hence larger prediction error. As applications proliferate, users must choose which precision to use to train a new model, and chip manufacturers must decide which precisions to manufacture. We view these precision choices as a hyperparameter tuning problem, and borrow ideas from meta-learning to learn the tradeoff between memory and error. In this paper, we introduce Pareto Estimation to Pick the Perfect Precision (PEPPP). We use matrix factorization to find non-dominated configurations (the Pareto frontier) with a limited number of network evaluations. For any given memory budget, the precision that minimizes error is a point on this frontier. Practitioners can use the frontier to trade memory for error and choose the best precision for their goals.

TenIPS: Inverse Propensity Sampling for Tensor Completion

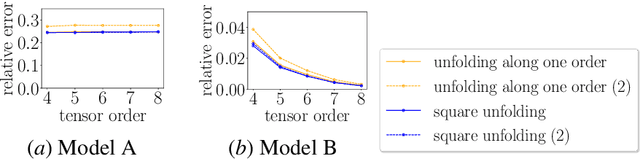
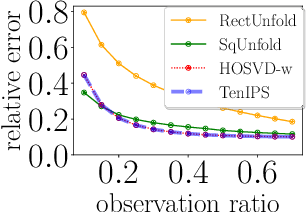
Tensors are widely used to represent multiway arrays of data. The recovery of missing entries in a tensor has been extensively studied, generally under the assumption that entries are missing completely at random (MCAR). However, in most practical settings, observations are missing not at random (MNAR): the probability that a given entry is observed (also called the propensity) may depend on other entries in the tensor or even on the value of the missing entry. In this paper, we study the problem of completing a partially observed tensor with MNAR observations, without prior information about the propensities. To complete the tensor, we assume that both the original tensor and the tensor of propensities have low multilinear rank. The algorithm first estimates the propensities using a convex relaxation and then predicts missing values using a higher-order SVD approach, reweighting the observed tensor by the inverse propensities. We provide finite-sample error bounds on the resulting complete tensor. Numerical experiments demonstrate the effectiveness of our approach.

Low-Rank Tensor Recovery with Euclidean-Norm-Induced Schatten-p Quasi-Norm Regularization

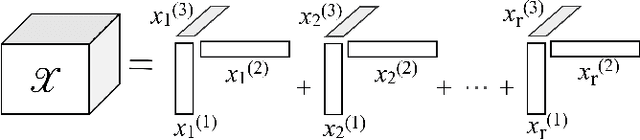
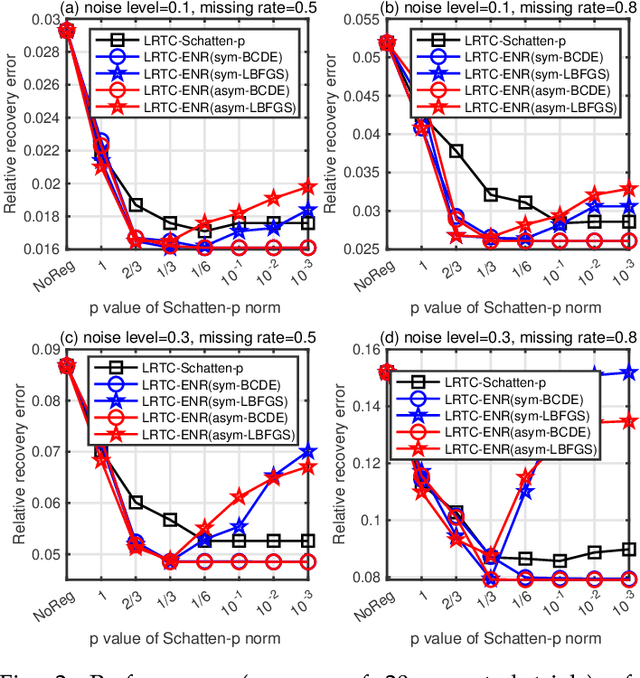
The nuclear norm and Schatten-$p$ quasi-norm of a matrix are popular rank proxies in low-rank matrix recovery. Unfortunately, computing the nuclear norm or Schatten-$p$ quasi-norm of a tensor is NP-hard, which is a pity for low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). In this paper, we propose a new class of rank regularizers based on the Euclidean norms of the CP component vectors of a tensor and show that these regularizers are monotonic transformations of tensor Schatten-$p$ quasi-norm. This connection enables us to minimize the Schatten-$p$ quasi-norm in LRTC and TRPCA implicitly. The methods do not use the singular value decomposition and hence scale to big tensors. Moreover, the methods are not sensitive to the choice of initial rank and provide an arbitrarily sharper rank proxy for low-rank tensor recovery compared to nuclear norm. We provide theoretical guarantees in terms of recovery error for LRTC and TRPCA, which show relatively smaller $p$ of Schatten-$p$ quasi-norm leads to tighter error bounds. Experiments using LRTC and TRPCA on synthetic data and natural images verify the effectiveness and superiority of our methods compared to baseline methods.

Efficient AutoML Pipeline Search with Matrix and Tensor Factorization

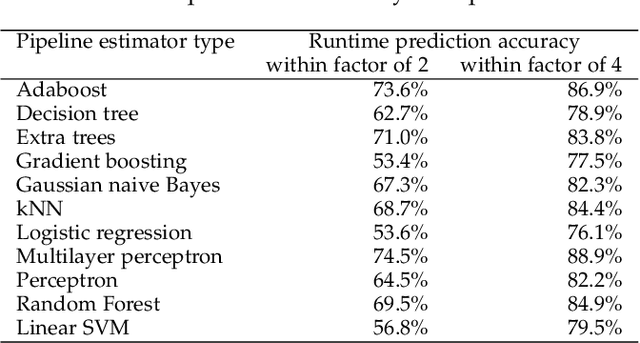
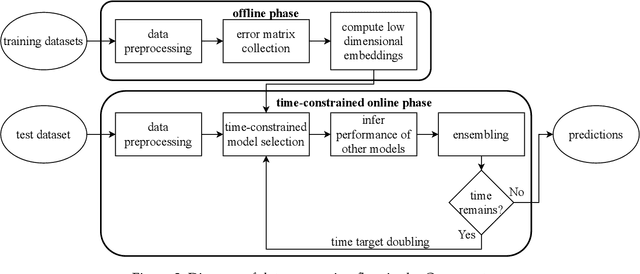
Data scientists seeking a good supervised learning model on a new dataset have many choices to make: they must preprocess the data, select features, possibly reduce the dimension, select an estimation algorithm, and choose hyperparameters for each of these pipeline components. With new pipeline components comes a combinatorial explosion in the number of choices! In this work, we design a new AutoML system to address this challenge: an automated system to design a supervised learning pipeline. Our system uses matrix and tensor factorization as surrogate models to model the combinatorial pipeline search space. Under these models, we develop greedy experiment design protocols to efficiently gather information about a new dataset. Experiments on large corpora of real-world classification problems demonstrate the effectiveness of our approach.

Robust Non-Linear Matrix Factorization for Dictionary Learning, Denoising, and Clustering

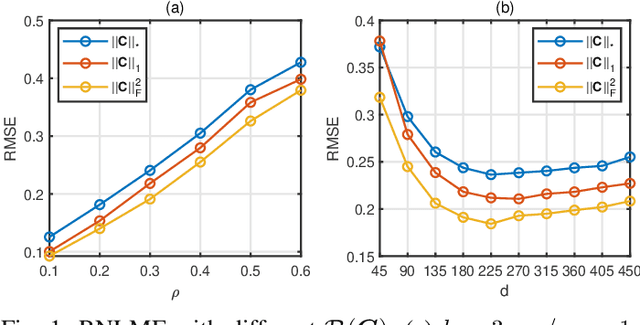
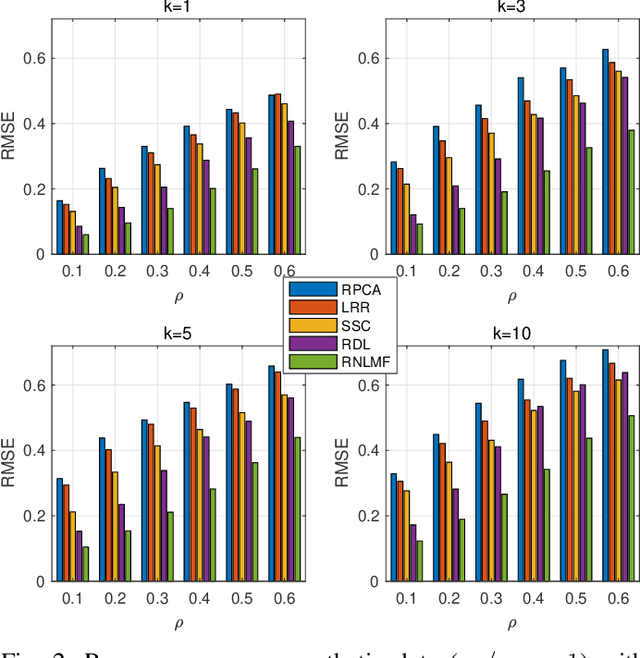
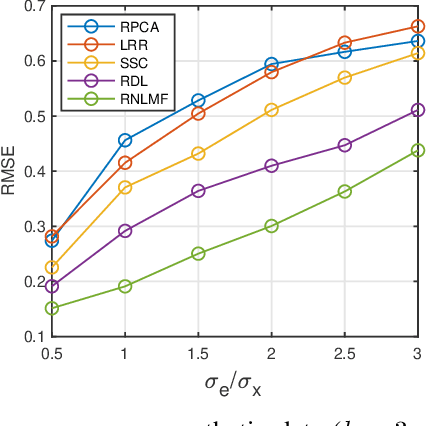
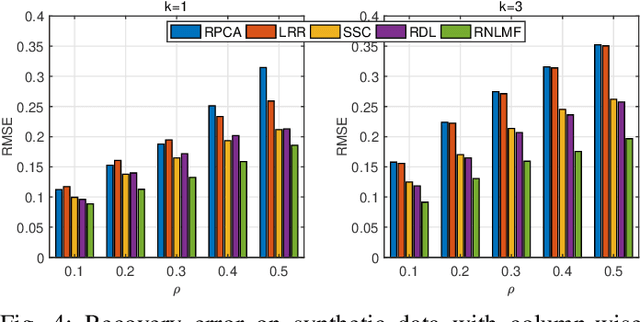
Low dimensional nonlinear structure abounds in datasets across computer vision and machine learning. Kernelized matrix factorization techniques have recently been proposed to learn these nonlinear structures from partially observed data, with impressive empirical performance, by observing that the image of the matrix in a sufficiently large feature space is low-rank. However, these nonlinear methods fail in the presence of noise or outliers. In this work, we propose a new robust nonlinear factorization method called Robust Non-Linear Matrix Factorization (RNLMF). RNLMF constructs a dictionary for the data space by factoring a kernelized feature space; a noisy matrix can then be decomposed as the sum of a sparse noise matrix and a clean data matrix that lies in a low dimensional nonlinear manifold. RNLMF is robust to noise and outliers and scales to matrices with thousands of rows and columns. Empirically, RNLMF achieves noticeable improvements over baseline methods in denoising and clustering.

OBOE: Collaborative Filtering for AutoML Initialization

Algorithm selection and hyperparameter tuning remain two of the most challenging tasks in machine learning. The number of machine learning applications is growing much faster than the number of machine learning experts, hence we see an increasing demand for efficient automation of learning processes. Here, we introduce OBOE, an algorithm for time-constrained model selection and hyperparameter tuning. Taking advantage of similarity between datasets, OBOE finds promising algorithm and hyperparameter configurations through collaborative filtering. Our system explores these models under time constraints, so that rapid initializations can be provided to warm-start more fine-grained optimization methods. One novel aspect of our approach is a new heuristic for active learning in time-constrained matrix completion based on optimal experiment design. Our experiments demonstrate that OBOE delivers state-of-the-art performance faster than competing approaches on a test bed of supervised learning problems.