Robust Non-Linear Matrix Factorization for Dictionary Learning, Denoising, and Clustering
Paper and Code
May 04, 2020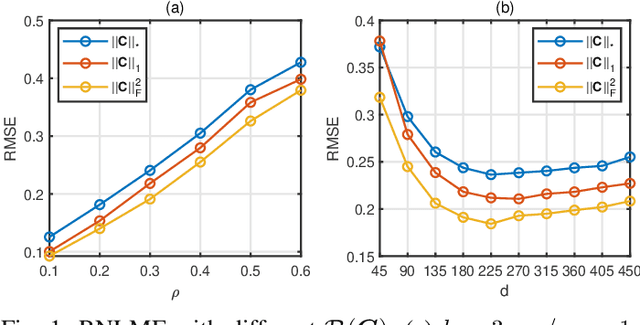
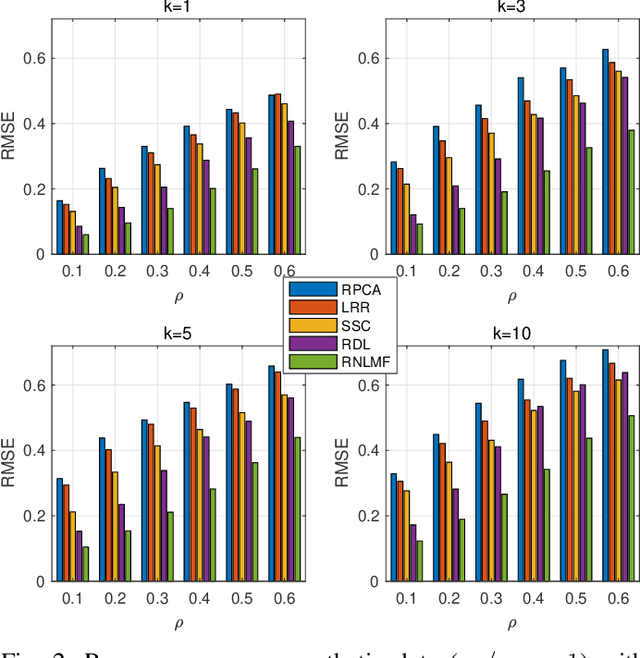
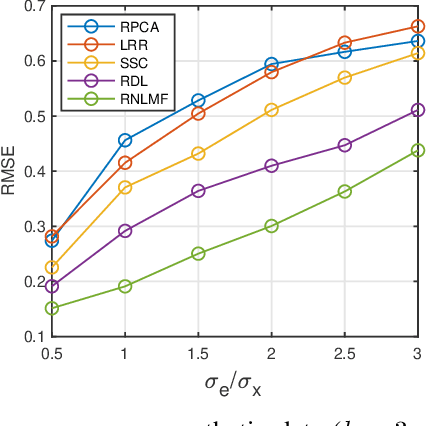
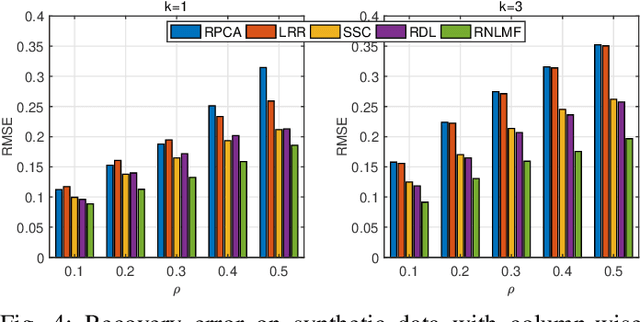
Low dimensional nonlinear structure abounds in datasets across computer vision and machine learning. Kernelized matrix factorization techniques have recently been proposed to learn these nonlinear structures from partially observed data, with impressive empirical performance, by observing that the image of the matrix in a sufficiently large feature space is low-rank. However, these nonlinear methods fail in the presence of noise or outliers. In this work, we propose a new robust nonlinear factorization method called Robust Non-Linear Matrix Factorization (RNLMF). RNLMF constructs a dictionary for the data space by factoring a kernelized feature space; a noisy matrix can then be decomposed as the sum of a sparse noise matrix and a clean data matrix that lies in a low dimensional nonlinear manifold. RNLMF is robust to noise and outliers and scales to matrices with thousands of rows and columns. Empirically, RNLMF achieves noticeable improvements over baseline methods in denoising and clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge