GraphProp: Training the Graph Foundation Models using Graph Properties

This work focuses on training graph foundation models (GFMs) that have strong generalization ability in graph-level tasks such as graph classification. Effective GFM training requires capturing information consistent across different domains. We discover that graph structures provide more consistent cross-domain information compared to node features and graph labels. However, traditional GFMs primarily focus on transferring node features from various domains into a unified representation space but often lack structural cross-domain generalization. To address this, we introduce GraphProp, which emphasizes structural generalization. The training process of GraphProp consists of two main phases. First, we train a structural GFM by predicting graph invariants. Since graph invariants are properties of graphs that depend only on the abstract structure, not on particular labellings or drawings of the graph, this structural GFM has a strong ability to capture the abstract structural information and provide discriminative graph representations comparable across diverse domains. In the second phase, we use the representations given by the structural GFM as positional encodings to train a comprehensive GFM. This phase utilizes domain-specific node attributes and graph labels to further improve cross-domain node feature generalization. Our experiments demonstrate that GraphProp significantly outperforms the competitors in supervised learning and few-shot learning, especially in handling graphs without node attributes.

Text-ADBench: Text Anomaly Detection Benchmark based on LLMs Embedding

Text anomaly detection is a critical task in natural language processing (NLP), with applications spanning fraud detection, misinformation identification, spam detection and content moderation, etc. Despite significant advances in large language models (LLMs) and anomaly detection algorithms, the absence of standardized and comprehensive benchmarks for evaluating the existing anomaly detection methods on text data limits rigorous comparison and development of innovative approaches. This work performs a comprehensive empirical study and introduces a benchmark for text anomaly detection, leveraging embeddings from diverse pre-trained language models across a wide array of text datasets. Our work systematically evaluates the effectiveness of embedding-based text anomaly detection by incorporating (1) early language models (GloVe, BERT); (2) multiple LLMs (LLaMa-2, LLama-3, Mistral, OpenAI (small, ada, large)); (3) multi-domain text datasets (news, social media, scientific publications); (4) comprehensive evaluation metrics (AUROC, AUPRC). Our experiments reveal a critical empirical insight: embedding quality significantly governs anomaly detection efficacy, and deep learning-based approaches demonstrate no performance advantage over conventional shallow algorithms (e.g., KNN, Isolation Forest) when leveraging LLM-derived embeddings.In addition, we observe strongly low-rank characteristics in cross-model performance matrices, which enables an efficient strategy for rapid model evaluation (or embedding evaluation) and selection in practical applications. Furthermore, by open-sourcing our benchmark toolkit that includes all embeddings from different models and code at https://github.com/jicongfan/Text-Anomaly-Detection-Benchmark, this work provides a foundation for future research in robust and scalable text anomaly detection systems.

UniOD: A Universal Model for Outlier Detection across Diverse Domains

Outlier detection (OD) seeks to distinguish inliers and outliers in completely unlabeled datasets and plays a vital role in science and engineering. Most existing OD methods require troublesome dataset-specific hyperparameter tuning and costly model training before they can be deployed to identify outliers. In this work, we propose UniOD, a universal OD framework that leverages labeled datasets to train a single model capable of detecting outliers of datasets from diverse domains. Specifically, UniOD converts each dataset into multiple graphs, produces consistent node features, and frames outlier detection as a node-classification task, and is able to generalize to unseen domains. As a result, UniOD avoids effort on model selection and hyperparameter tuning, reduces computational cost, and effectively utilizes the knowledge from historical datasets, which improves the convenience and accuracy in real applications. We evaluate UniOD on 15 benchmark OD datasets against 15 state-of-the-art baselines, demonstrating its effectiveness.

Learnable Kernel Density Estimation for Graphs

This work proposes a framework LGKDE that learns kernel density estimation for graphs. The key challenge in graph density estimation lies in effectively capturing both structural patterns and semantic variations while maintaining theoretical guarantees. Combining graph kernels and kernel density estimation (KDE) is a standard approach to graph density estimation, but has unsatisfactory performance due to the handcrafted and fixed features of kernels. Our method LGKDE leverages graph neural networks to represent each graph as a discrete distribution and utilizes maximum mean discrepancy to learn the graph metric for multi-scale KDE, where all parameters are learned by maximizing the density of graphs relative to the density of their well-designed perturbed counterparts. The perturbations are conducted on both node features and graph spectra, which helps better characterize the boundary of normal density regions. Theoretically, we establish consistency and convergence guarantees for LGKDE, including bounds on the mean integrated squared error, robustness, and complexity. We validate LGKDE by demonstrating its effectiveness in recovering the underlying density of synthetic graph distributions and applying it to graph anomaly detection across diverse benchmark datasets. Extensive empirical evaluation shows that LGKDE demonstrates superior performance compared to state-of-the-art baselines on most benchmark datasets.

Fairness-aware Anomaly Detection via Fair Projection

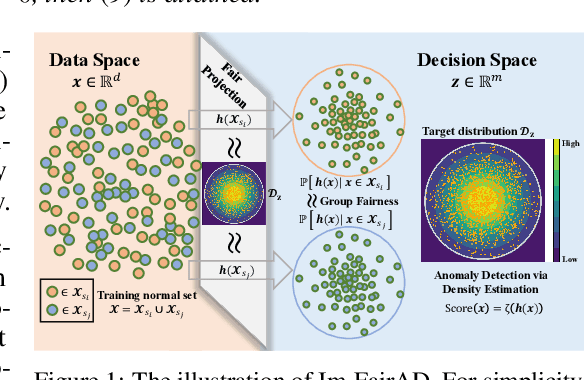
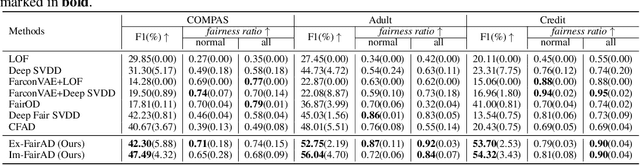
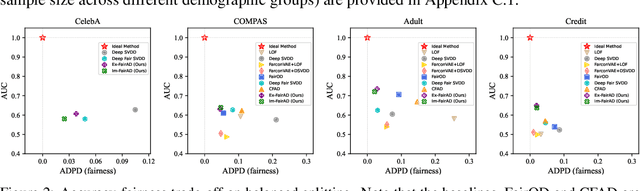
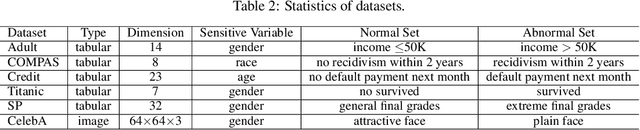
Unsupervised anomaly detection is a critical task in many high-social-impact applications such as finance, healthcare, social media, and cybersecurity, where demographics involving age, gender, race, disease, etc, are used frequently. In these scenarios, possible bias from anomaly detection systems can lead to unfair treatment for different groups and even exacerbate social bias. In this work, first, we thoroughly analyze the feasibility and necessary assumptions for ensuring group fairness in unsupervised anomaly detection. Second, we propose a novel fairness-aware anomaly detection method FairAD. From the normal training data, FairAD learns a projection to map data of different demographic groups to a common target distribution that is simple and compact, and hence provides a reliable base to estimate the density of the data. The density can be directly used to identify anomalies while the common target distribution ensures fairness between different groups. Furthermore, we propose a threshold-free fairness metric that provides a global view for model's fairness, eliminating dependence on manual threshold selection. Experiments on real-world benchmarks demonstrate that our method achieves an improved trade-off between detection accuracy and fairness under both balanced and skewed data across different groups.

Subject Information Extraction for Novelty Detection with Domain Shifts

Unsupervised novelty detection (UND), aimed at identifying novel samples, is essential in fields like medical diagnosis, cybersecurity, and industrial quality control. Most existing UND methods assume that the training data and testing normal data originate from the same domain and only consider the distribution variation between training data and testing data. However, in real scenarios, it is common for normal testing and training data to originate from different domains, a challenge known as domain shift. The discrepancies between training and testing data often lead to incorrect classification of normal data as novel by existing methods. A typical situation is that testing normal data and training data describe the same subject, yet they differ in the background conditions. To address this problem, we introduce a novel method that separates subject information from background variation encapsulating the domain information to enhance detection performance under domain shifts. The proposed method minimizes the mutual information between the representations of the subject and background while modelling the background variation using a deep Gaussian mixture model, where the novelty detection is conducted on the subject representations solely and hence is not affected by the variation of domains. Extensive experiments demonstrate that our model generalizes effectively to unseen domains and significantly outperforms baseline methods, especially under substantial domain shifts between training and testing data.

FCBoost-Net: A Generative Network for Synthesizing Multiple Collocated Outfits via Fashion Compatibility Boosting

Outfit generation is a challenging task in the field of fashion technology, in which the aim is to create a collocated set of fashion items that complement a given set of items. Previous studies in this area have been limited to generating a unique set of fashion items based on a given set of items, without providing additional options to users. This lack of a diverse range of choices necessitates the development of a more versatile framework. However, when the task of generating collocated and diversified outfits is approached with multimodal image-to-image translation methods, it poses a challenging problem in terms of non-aligned image translation, which is hard to address with existing methods. In this research, we present FCBoost-Net, a new framework for outfit generation that leverages the power of pre-trained generative models to produce multiple collocated and diversified outfits. Initially, FCBoost-Net randomly synthesizes multiple sets of fashion items, and the compatibility of the synthesized sets is then improved in several rounds using a novel fashion compatibility booster. This approach was inspired by boosting algorithms and allows the performance to be gradually improved in multiple steps. Empirical evidence indicates that the proposed strategy can improve the fashion compatibility of randomly synthesized fashion items as well as maintain their diversity. Extensive experiments confirm the effectiveness of our proposed framework with respect to visual authenticity, diversity, and fashion compatibility.

Mutual Regression Distance

The maximum mean discrepancy and Wasserstein distance are popular distance measures between distributions and play important roles in many machine learning problems such as metric learning, generative modeling, domain adaption, and clustering. However, since they are functions of pair-wise distances between data points in two distributions, they do not exploit the potential manifold properties of data such as smoothness and hence are not effective in measuring the dissimilarity between the two distributions in the form of manifolds. In this paper, different from existing measures, we propose a novel distance called Mutual Regression Distance (MRD) induced by a constrained mutual regression problem, which can exploit the manifold property of data. We prove that MRD is a pseudometric that satisfies almost all the axioms of a metric. Since the optimization of the original MRD is costly, we provide a tight MRD and a simplified MRD, based on which a heuristic algorithm is established. We also provide kernel variants of MRDs that are more effective in handling nonlinear data. Our MRDs especially the simplified MRDs have much lower computational complexity than the Wasserstein distance. We provide theoretical guarantees, such as robustness, for MRDs. Finally, we apply MRDs to distribution clustering, generative models, and domain adaptation. The numerical results demonstrate the effectiveness and superiority of MRDs compared to the baselines.

Non-Convex Tensor Recovery from Local Measurements

Motivated by the settings where sensing the entire tensor is infeasible, this paper proposes a novel tensor compressed sensing model, where measurements are only obtained from sensing each lateral slice via mutually independent matrices. Leveraging the low tubal rank structure, we reparameterize the unknown tensor ${\boldsymbol {\mathcal X}}^\star$ using two compact tensor factors and formulate the recovery problem as a nonconvex minimization problem. To solve the problem, we first propose an alternating minimization algorithm, termed \textsf{Alt-PGD-Min}, that iteratively optimizes the two factors using a projected gradient descent and an exact minimization step, respectively. Despite nonconvexity, we prove that \textsf{Alt-PGD-Min} achieves $\epsilon$-accuracy recovery with $\mathcal O\left( \kappa^2 \log \frac{1}{\epsilon}\right)$ iteration complexity and $\mathcal O\left( \kappa^6rn_3\log n_3 \left( \kappa^2r\left(n_1 + n_2 \right) + n_1 \log \frac{1}{\epsilon}\right) \right)$ sample complexity, where $\kappa$ denotes tensor condition number of $\boldsymbol{\mathcal X}^\star$. To further accelerate the convergence, especially when the tensor is ill-conditioned with large $\kappa$, we prove \textsf{Alt-ScalePGD-Min} that preconditions the gradient update using an approximate Hessian that can be computed efficiently. We show that \textsf{Alt-ScalePGD-Min} achieves $\kappa$ independent iteration complexity $\mathcal O(\log \frac{1}{\epsilon})$ and improves the sample complexity to $\mathcal O\left( \kappa^4 rn_3 \log n_3 \left( \kappa^4r(n_1+n_2) + n_1 \log \frac{1}{\epsilon}\right) \right)$. Experiments validate the effectiveness of the proposed methods.

Federated t-SNE and UMAP for Distributed Data Visualization

High-dimensional data visualization is crucial in the big data era and these techniques such as t-SNE and UMAP have been widely used in science and engineering. Big data, however, is often distributed across multiple data centers and subject to security and privacy concerns, which leads to difficulties for the standard algorithms of t-SNE and UMAP. To tackle the challenge, this work proposes Fed-tSNE and Fed-UMAP, which provide high-dimensional data visualization under the framework of federated learning, without exchanging data across clients or sending data to the central server. The main idea of Fed-tSNE and Fed-UMAP is implicitly learning the distribution information of data in a manner of federated learning and then estimating the global distance matrix for t-SNE and UMAP. To further enhance the protection of data privacy, we propose Fed-tSNE+ and Fed-UMAP+. We also extend our idea to federated spectral clustering, yielding algorithms of clustering distributed data. In addition to these new algorithms, we offer theoretical guarantees of optimization convergence, distance and similarity estimation, and differential privacy. Experiments on multiple datasets demonstrate that, compared to the original algorithms, the accuracy drops of our federated algorithms are tiny.