How Low Can We Go: Trading Memory for Error in Low-Precision Training
Paper and Code
Jun 18, 2021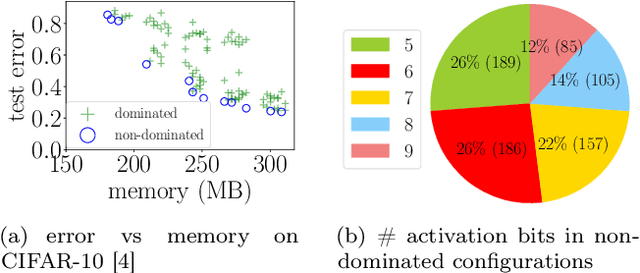
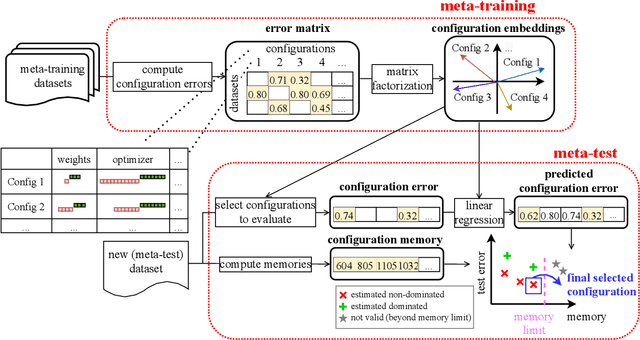
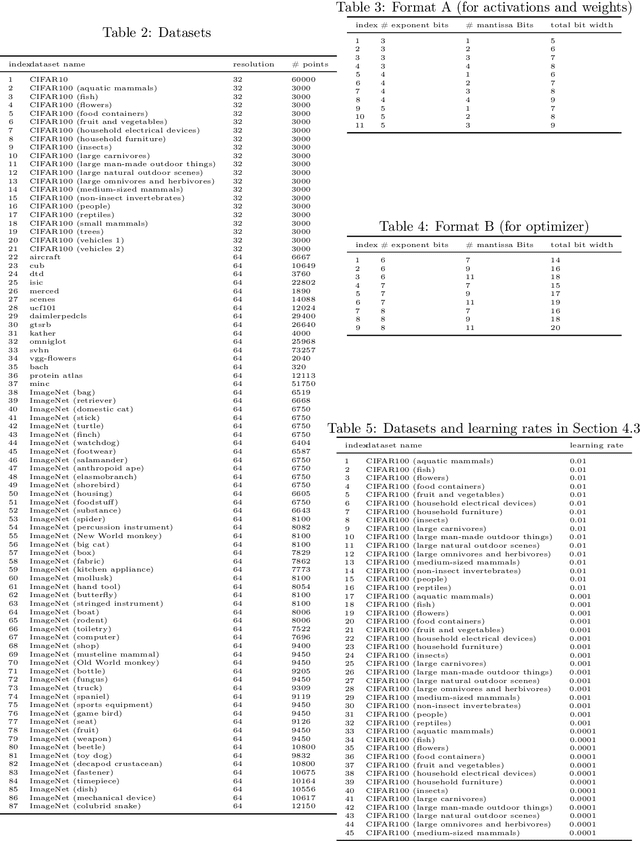
Low-precision arithmetic trains deep learning models using less energy, less memory and less time. However, we pay a price for the savings: lower precision may yield larger round-off error and hence larger prediction error. As applications proliferate, users must choose which precision to use to train a new model, and chip manufacturers must decide which precisions to manufacture. We view these precision choices as a hyperparameter tuning problem, and borrow ideas from meta-learning to learn the tradeoff between memory and error. In this paper, we introduce Pareto Estimation to Pick the Perfect Precision (PEPPP). We use matrix factorization to find non-dominated configurations (the Pareto frontier) with a limited number of network evaluations. For any given memory budget, the precision that minimizes error is a point on this frontier. Practitioners can use the frontier to trade memory for error and choose the best precision for their goals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge