DiscQuant: A Quantization Method for Neural Networks Inspired by Discrepancy Theory

Quantizing the weights of a neural network has two steps: (1) Finding a good low bit-complexity representation for weights (which we call the quantization grid) and (2) Rounding the original weights to values in the quantization grid. In this paper, we study the problem of rounding optimally given any quantization grid. The simplest and most commonly used way to round is Round-to-Nearest (RTN). By rounding in a data-dependent way instead, one can improve the quality of the quantized model significantly. We study the rounding problem from the lens of \emph{discrepancy theory}, which studies how well we can round a continuous solution to a discrete solution without affecting solution quality too much. We prove that given $m=\mathrm{poly}(1/\epsilon)$ samples from the data distribution, we can round all but $O(m)$ model weights such that the expected approximation error of the quantized model on the true data distribution is $\le \epsilon$ as long as the space of gradients of the original model is approximately low rank (which we empirically validate). Our proof, which is algorithmic, inspired a simple and practical rounding algorithm called \emph{DiscQuant}. In our experiments, we demonstrate that DiscQuant significantly improves over the prior state-of-the-art rounding method called GPTQ and the baseline RTN over a range of benchmarks on Phi3mini-3.8B and Llama3.1-8B. For example, rounding Phi3mini-3.8B to a fixed quantization grid with 3.25 bits per parameter using DiscQuant gets 64\% accuracy on the GSM8k dataset, whereas GPTQ achieves 54\% and RTN achieves 31\% (the original model achieves 84\%). We make our code available at https://github.com/jerry-chee/DiscQuant.

Harm Mitigation in Recommender Systems under User Preference Dynamics

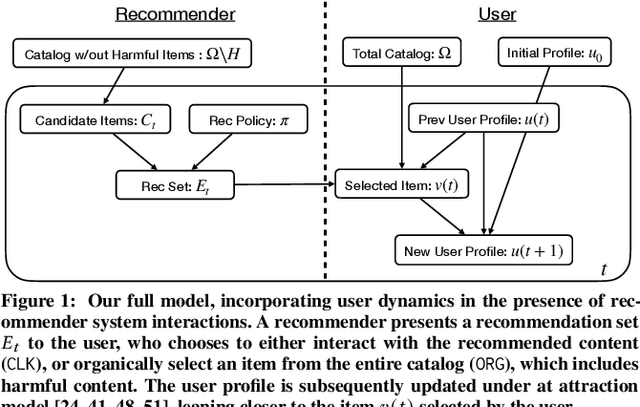
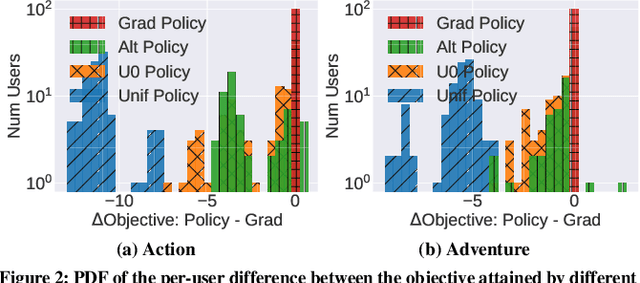
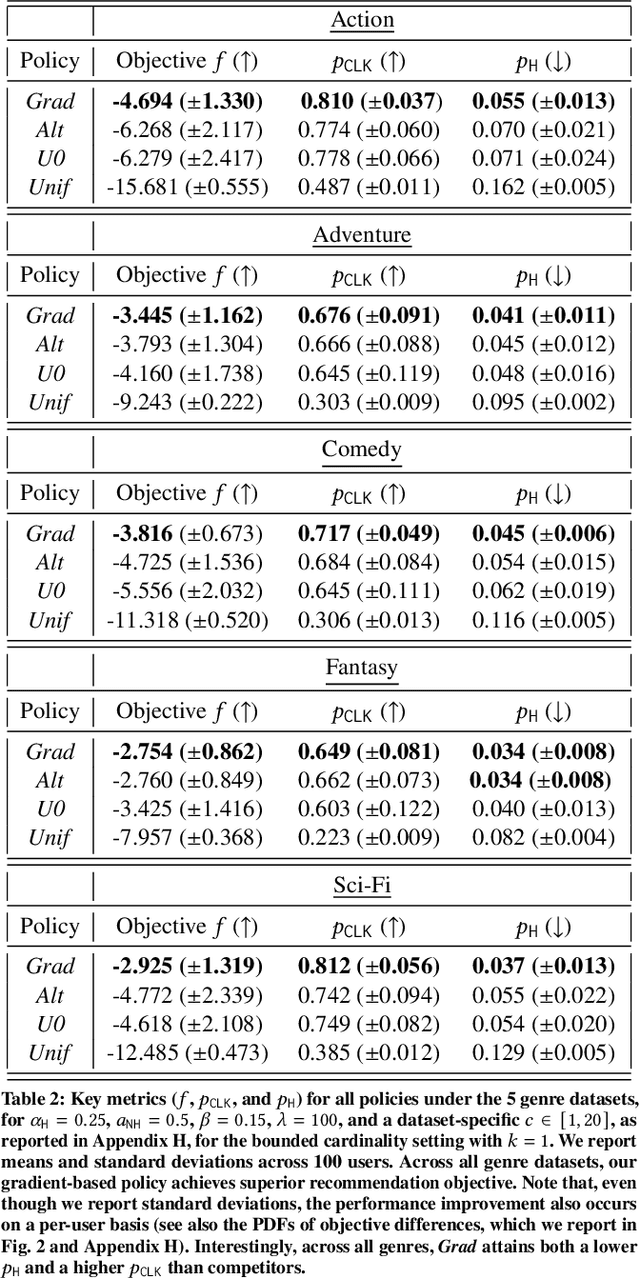
We consider a recommender system that takes into account the interplay between recommendations, the evolution of user interests, and harmful content. We model the impact of recommendations on user behavior, particularly the tendency to consume harmful content. We seek recommendation policies that establish a tradeoff between maximizing click-through rate (CTR) and mitigating harm. We establish conditions under which the user profile dynamics have a stationary point, and propose algorithms for finding an optimal recommendation policy at stationarity. We experiment on a semi-synthetic movie recommendation setting initialized with real data and observe that our policies outperform baselines at simultaneously maximizing CTR and mitigating harm.

QuIP#: Even Better LLM Quantization with Hadamard Incoherence and Lattice Codebooks

Post-training quantization (PTQ) reduces the memory footprint of LLMs by quantizing their weights to low-precision. In this work, we introduce QuIP#, a weight-only PTQ method that achieves state-of-the-art results in extreme compression regimes ($\le$ 4 bits per weight) using three novel techniques. First, QuIP# improves the incoherence processing from QuIP by using the randomized Hadamard transform, which is faster and has better theoretical properties. Second, QuIP# uses vector quantization techniques to take advantage of the ball-shaped sub-Gaussian distribution that incoherent weights possess: specifically, we introduce a set of hardware-efficient codebooks based on the highly symmetric $E_8$ lattice, which achieves the optimal 8-dimension unit ball packing. Third, QuIP# uses fine-tuning to improve fidelity to the original model. Our experiments show that QuIP# outperforms existing PTQ methods, enables new behaviors in PTQ scaling, and supports fast inference.

QuIP: 2-Bit Quantization of Large Language Models With Guarantees

This work studies post-training parameter quantization in large language models (LLMs). We introduce quantization with incoherence processing (QuIP), a new method based on the insight that quantization benefits from incoherent weight and Hessian matrices, i.e., from the weights and the directions in which it is important to round them accurately being unaligned with the coordinate axes. QuIP consists of two steps: (1) an adaptive rounding procedure minimizing a quadratic proxy objective; (2) efficient pre- and post-processing that ensures weight and Hessian incoherence via multiplication by random orthogonal matrices. We complement QuIP with the first theoretical analysis for an LLM-scale quantization algorithm, and show that our theory also applies to an existing method, OPTQ. Empirically, we find that our incoherence preprocessing improves several existing quantization algorithms and yields the first LLM quantization methods that produce viable results using only two bits per weight. Our code can be found at https://github.com/jerry-chee/QuIP .

Performance optimizations on deep noise suppression models

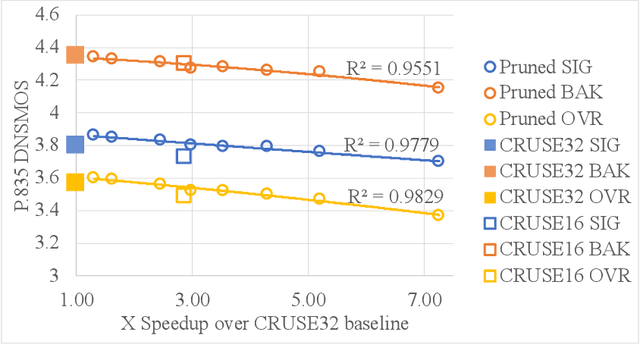
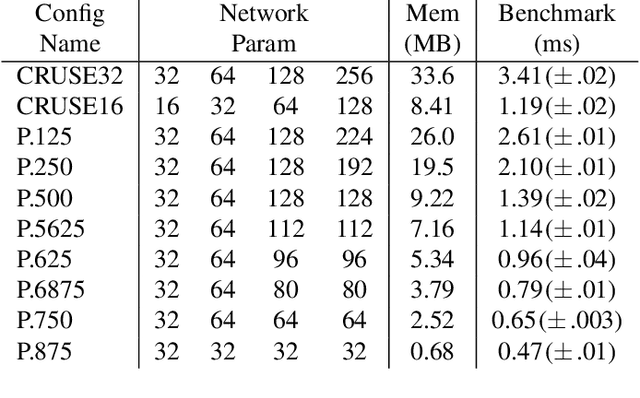
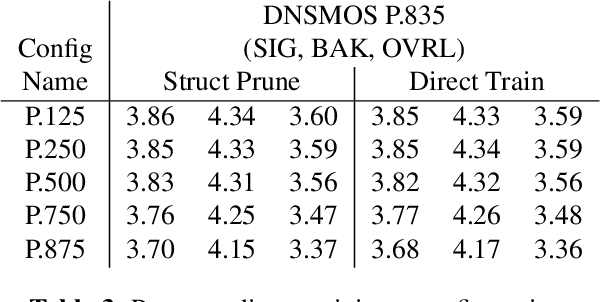
We study the role of magnitude structured pruning as an architecture search to speed up the inference time of a deep noise suppression (DNS) model. While deep learning approaches have been remarkably successful in enhancing audio quality, their increased complexity inhibits their deployment in real-time applications. We achieve up to a 7.25X inference speedup over the baseline, with a smooth model performance degradation. Ablation studies indicate that our proposed network re-parameterization (i.e., size per layer) is the major driver of the speedup, and that magnitude structured pruning does comparably to directly training a model in the smaller size. We report inference speed because a parameter reduction does not necessitate speedup, and we measure model quality using an accurate non-intrusive objective speech quality metric.

Pruning Neural Networks with Interpolative Decompositions

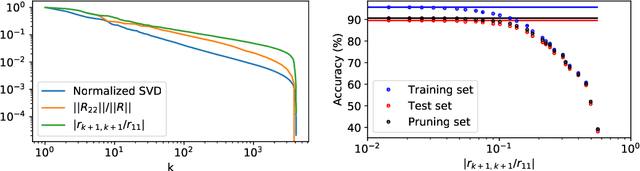
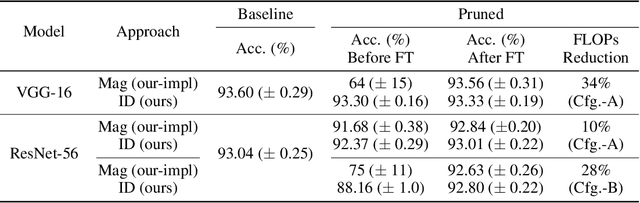
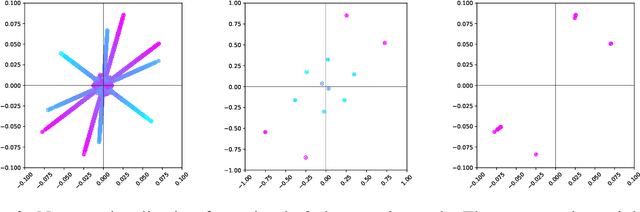
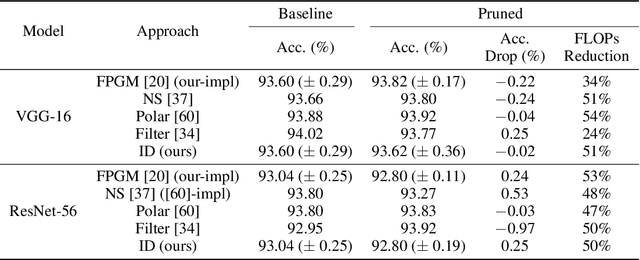
We introduce a principled approach to neural network pruning that casts the problem as a structured low-rank matrix approximation. Our method uses a novel application of a matrix factorization technique called the interpolative decomposition to approximate the activation output of a network layer. This technique selects neurons or channels in the layer and propagates a corrective interpolation matrix to the next layer, resulting in a dense, pruned network with minimal degradation before fine tuning. We demonstrate how to prune a neural network by first building a set of primitives to prune a single fully connected or convolution layer and then composing these primitives to prune deep multi-layer networks. Theoretical guarantees are provided for pruning a single hidden layer fully connected network. Pruning with interpolative decompositions achieves strong empirical results compared to the state-of-the-art on multiple applications from one and two hidden layer networks on Fashion MNIST to VGG and ResNets on CIFAR-10. Notably, we achieve an accuracy of 93.62 $\pm$ 0.36% using VGG-16 on CIFAR-10, with a 51% FLOPS reduction. This gains 0.02% from the full-sized model.

How Low Can We Go: Trading Memory for Error in Low-Precision Training

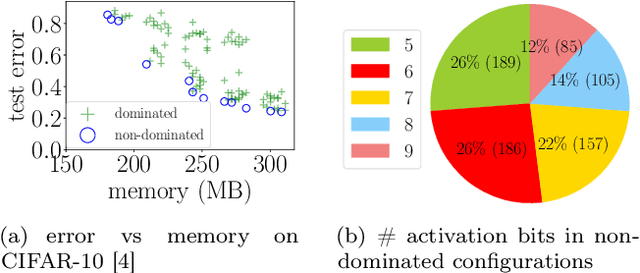
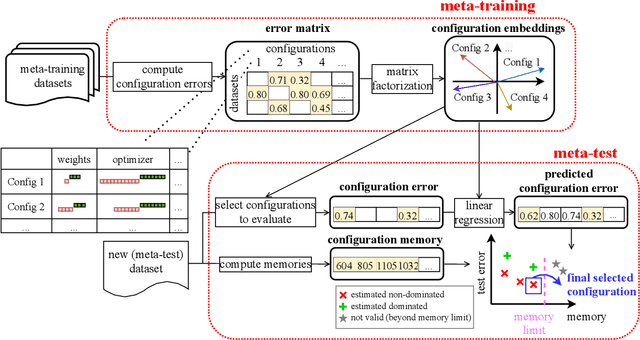
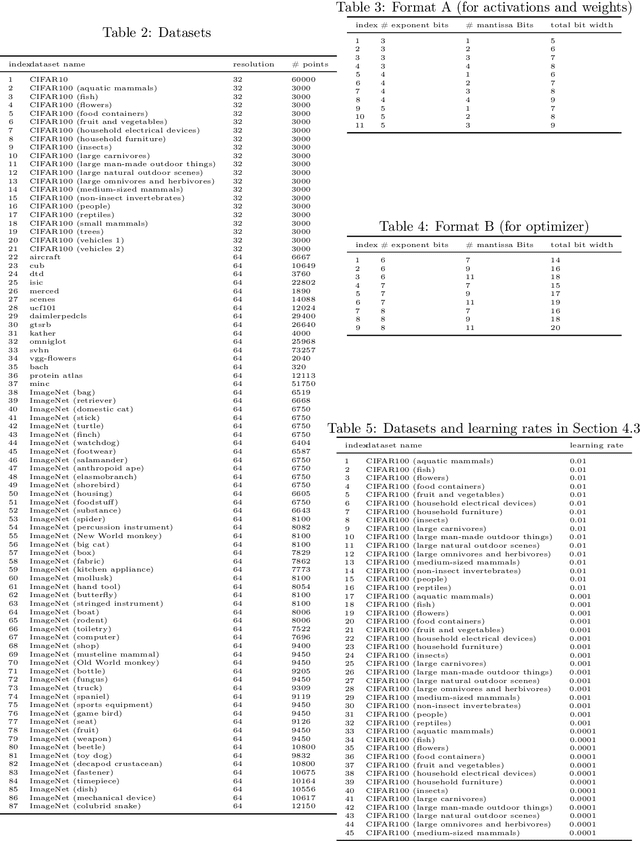
Low-precision arithmetic trains deep learning models using less energy, less memory and less time. However, we pay a price for the savings: lower precision may yield larger round-off error and hence larger prediction error. As applications proliferate, users must choose which precision to use to train a new model, and chip manufacturers must decide which precisions to manufacture. We view these precision choices as a hyperparameter tuning problem, and borrow ideas from meta-learning to learn the tradeoff between memory and error. In this paper, we introduce Pareto Estimation to Pick the Perfect Precision (PEPPP). We use matrix factorization to find non-dominated configurations (the Pareto frontier) with a limited number of network evaluations. For any given memory budget, the precision that minimizes error is a point on this frontier. Practitioners can use the frontier to trade memory for error and choose the best precision for their goals.

Understanding and Detecting Convergence for Stochastic Gradient Descent with Momentum

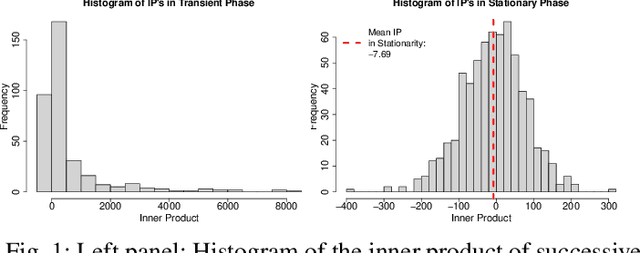
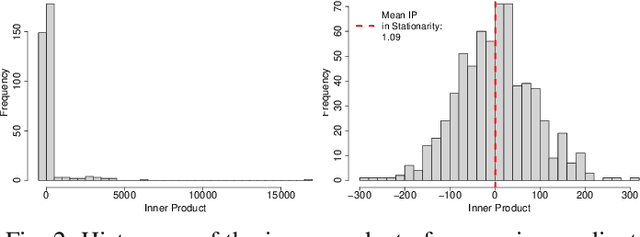
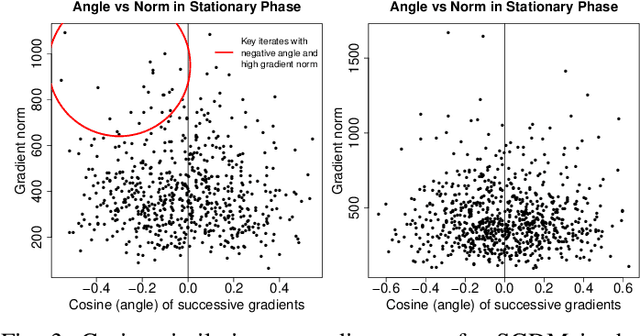
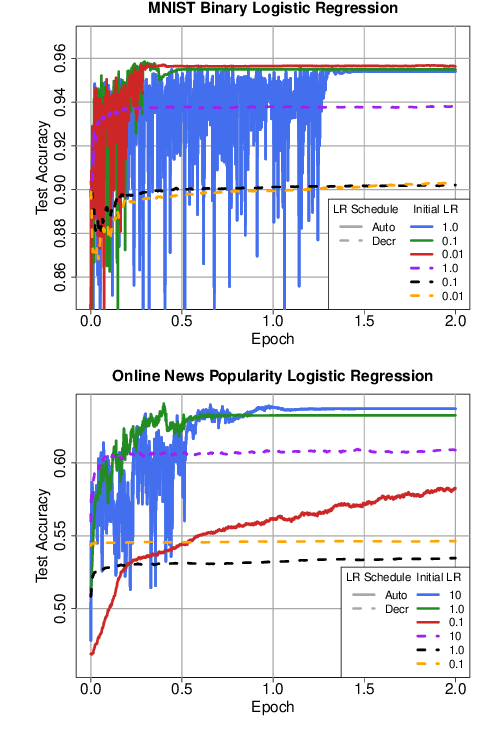
Convergence detection of iterative stochastic optimization methods is of great practical interest. This paper considers stochastic gradient descent (SGD) with a constant learning rate and momentum. We show that there exists a transient phase in which iterates move towards a region of interest, and a stationary phase in which iterates remain bounded in that region around a minimum point. We construct a statistical diagnostic test for convergence to the stationary phase using the inner product between successive gradients and demonstrate that the proposed diagnostic works well. We theoretically and empirically characterize how momentum can affect the test statistic of the diagnostic, and how the test statistic captures a relatively sparse signal within the gradients in convergence. Finally, we demonstrate an application to automatically tune the learning rate by reducing it each time stationarity is detected, and show the procedure is robust to mis-specified initial rates.

Convergence diagnostics for stochastic gradient descent with constant step size

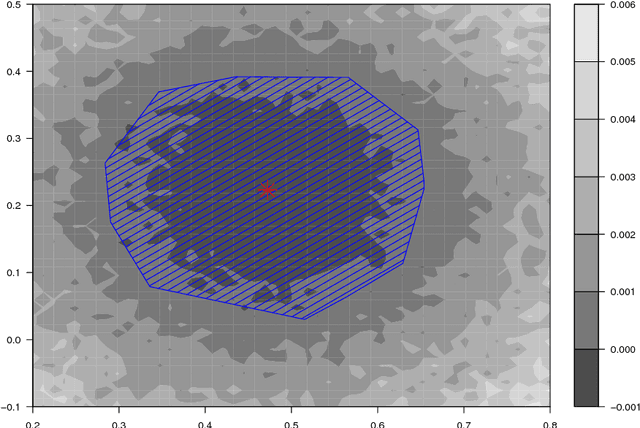
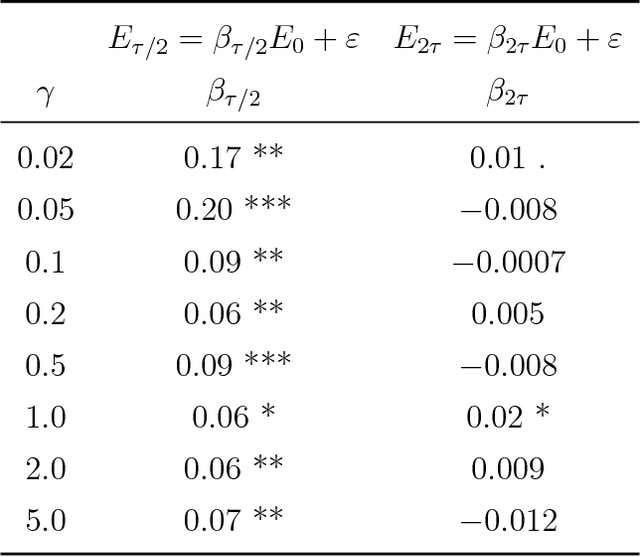
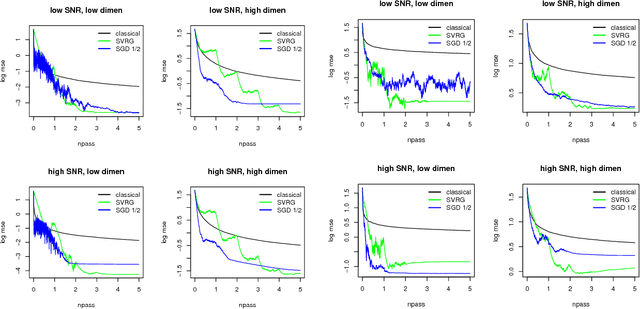
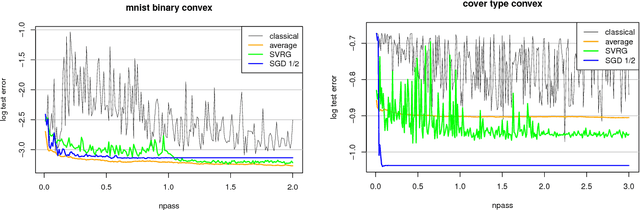
Many iterative procedures in stochastic optimization exhibit a transient phase followed by a stationary phase. During the transient phase the procedure converges towards a region of interest, and during the stationary phase the procedure oscillates in that region, commonly around a single point. In this paper, we develop a statistical diagnostic test to detect such phase transition in the context of stochastic gradient descent with constant learning rate. We present theory and experiments suggesting that the region where the proposed diagnostic is activated coincides with the convergence region. For a class of loss functions, we derive a closed-form solution describing such region. Finally, we suggest an application to speed up convergence of stochastic gradient descent by halving the learning rate each time stationarity is detected. This leads to a new variant of stochastic gradient descent, which in many settings is comparable to state-of-art.