Diffusion Models With Learned Adaptive Noise

Diffusion models have gained traction as powerful algorithms for synthesizing high-quality images. Central to these algorithms is the diffusion process, which maps data to noise according to equations inspired by thermodynamics and can significantly impact performance. A widely held assumption is that the ELBO objective of a diffusion model is invariant to the noise process (Kingma et al.,2021). In this work, we dispel this assumption -- we propose multivariate learned adaptive noise (MuLAN), a learned diffusion process that applies Gaussian noise at different rates across an image. Our method consists of three components -- a multivariate noise schedule, instance-conditional diffusion, and auxiliary variables -- which ensure that the learning objective is no longer invariant to the choice of the noise schedule as in previous works. Our work is grounded in Bayesian inference and casts the learned diffusion process as an approximate variational posterior that yields a tighter lower bound on marginal likelihood. Empirically, MuLAN sets a new state-of-the-art in density estimation on CIFAR-10 and ImageNet compared to classical diffusion. Code is available at https://github.com/s-sahoo/MuLAN

From Gradient Flow on Population Loss to Learning with Stochastic Gradient Descent

Stochastic Gradient Descent (SGD) has been the method of choice for learning large-scale non-convex models. While a general analysis of when SGD works has been elusive, there has been a lot of recent progress in understanding the convergence of Gradient Flow (GF) on the population loss, partly due to the simplicity that a continuous-time analysis buys us. An overarching theme of our paper is providing general conditions under which SGD converges, assuming that GF on the population loss converges. Our main tool to establish this connection is a general converse Lyapunov like theorem, which implies the existence of a Lyapunov potential under mild assumptions on the rates of convergence of GF. In fact, using these potentials, we show a one-to-one correspondence between rates of convergence of GF and geometrical properties of the underlying objective. When these potentials further satisfy certain self-bounding properties, we show that they can be used to provide a convergence guarantee for Gradient Descent (GD) and SGD (even when the paths of GF and GD/SGD are quite far apart). It turns out that these self-bounding assumptions are in a sense also necessary for GD/SGD to work. Using our framework, we provide a unified analysis for GD/SGD not only for classical settings like convex losses, or objectives that satisfy PL / KL properties, but also for more complex problems including Phase Retrieval and Matrix sq-root, and extending the results in the recent work of Chatterjee 2022.

Pruning Neural Networks with Interpolative Decompositions

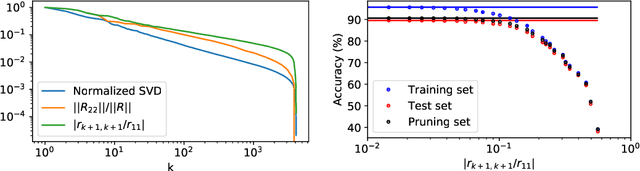
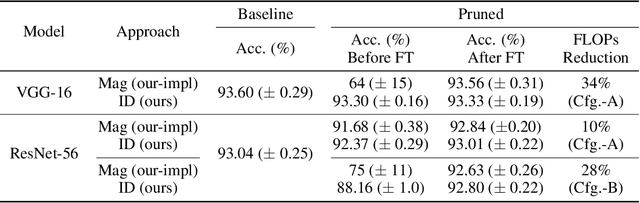
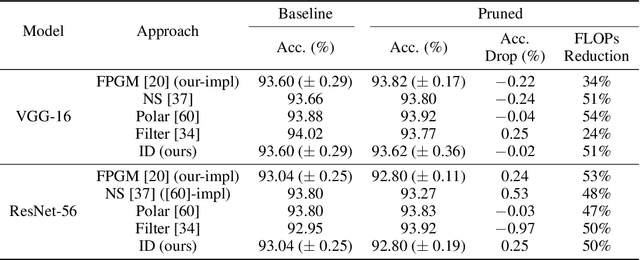
We introduce a principled approach to neural network pruning that casts the problem as a structured low-rank matrix approximation. Our method uses a novel application of a matrix factorization technique called the interpolative decomposition to approximate the activation output of a network layer. This technique selects neurons or channels in the layer and propagates a corrective interpolation matrix to the next layer, resulting in a dense, pruned network with minimal degradation before fine tuning. We demonstrate how to prune a neural network by first building a set of primitives to prune a single fully connected or convolution layer and then composing these primitives to prune deep multi-layer networks. Theoretical guarantees are provided for pruning a single hidden layer fully connected network. Pruning with interpolative decompositions achieves strong empirical results compared to the state-of-the-art on multiple applications from one and two hidden layer networks on Fashion MNIST to VGG and ResNets on CIFAR-10. Notably, we achieve an accuracy of 93.62 $\pm$ 0.36% using VGG-16 on CIFAR-10, with a 51% FLOPS reduction. This gains 0.02% from the full-sized model.

Model Selection's Disparate Impact in Real-World Deep Learning Applications

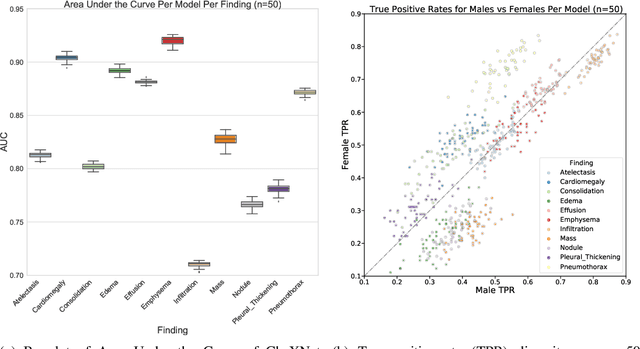
Algorithmic fairness has emphasized the role of biased data in automated decision outcomes. Recently, there has been a shift in attention to sources of bias that implicate fairness in other stages in the ML pipeline. We contend that one source of such bias, human preferences in model selection, remains under-explored in terms of its role in disparate impact across demographic groups. Using a deep learning model trained on real-world medical imaging data, we verify our claim empirically and argue that choice of metric for model comparison can significantly bias model selection outcomes.