STAT: Shrinking Transformers After Training

We present STAT: a simple algorithm to prune transformer models without any fine-tuning. STAT eliminates both attention heads and neurons from the network, while preserving accuracy by calculating a correction to the weights of the next layer. Each layer block in the network is compressed using a series of principled matrix factorizations that preserve the network structure. Our entire algorithm takes minutes to compress BERT, and less than three hours to compress models with 7B parameters using a single GPU. Using only several hundred data examples, STAT preserves the output of the network and improves upon existing gradient-free pruning methods. It is even competitive with methods that include significant fine-tuning. We demonstrate our method on both encoder and decoder architectures, including BERT, DistilBERT, and Llama-2 using benchmarks such as GLUE, Squad, WikiText2.

Communication-efficient distributed eigenspace estimation with arbitrary node failures

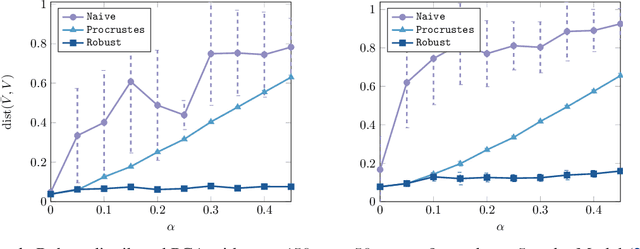
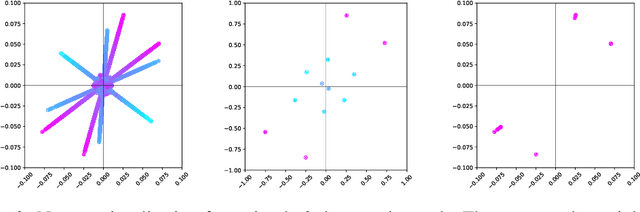
We develop an eigenspace estimation algorithm for distributed environments with arbitrary node failures, where a subset of computing nodes can return structurally valid but otherwise arbitrarily chosen responses. Notably, this setting encompasses several important scenarios that arise in distributed computing and data-collection environments such as silent/soft errors, outliers or corrupted data at certain nodes, and adversarial responses. Our estimator builds upon and matches the performance of a recently proposed non-robust estimator up to an additive $\tilde{O}(\sigma \sqrt{\alpha})$ error, where $\sigma^2$ is the variance of the existing estimator and $\alpha$ is the fraction of corrupted nodes.

Linear Time Kernel Matrix Approximation via Hyperspherical Harmonics

We propose a new technique for constructing low-rank approximations of matrices that arise in kernel methods for machine learning. Our approach pairs a novel automatically constructed analytic expansion of the underlying kernel function with a data-dependent compression step to further optimize the approximation. This procedure works in linear time and is applicable to any isotropic kernel. Moreover, our method accepts the desired error tolerance as input, in contrast to prevalent methods which accept the rank as input. Experimental results show our approach compares favorably to the commonly used Nystrom method with respect to both accuracy for a given rank and computational time for a given accuracy across a variety of kernels, dimensions, and datasets. Notably, in many of these problem settings our approach produces near-optimal low-rank approximations. We provide an efficient open-source implementation of our new technique to complement our theoretical developments and experimental results.

Pruning Neural Networks with Interpolative Decompositions

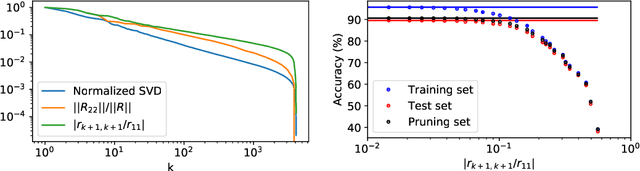
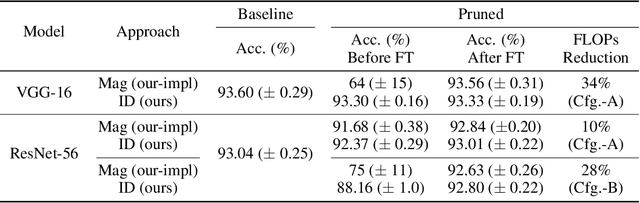
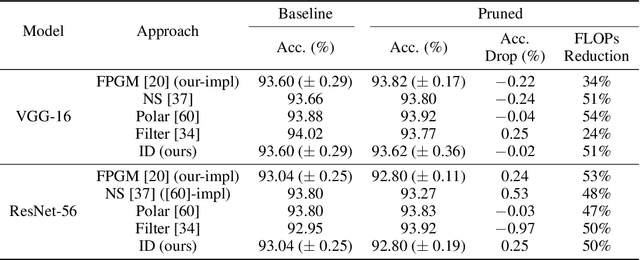
We introduce a principled approach to neural network pruning that casts the problem as a structured low-rank matrix approximation. Our method uses a novel application of a matrix factorization technique called the interpolative decomposition to approximate the activation output of a network layer. This technique selects neurons or channels in the layer and propagates a corrective interpolation matrix to the next layer, resulting in a dense, pruned network with minimal degradation before fine tuning. We demonstrate how to prune a neural network by first building a set of primitives to prune a single fully connected or convolution layer and then composing these primitives to prune deep multi-layer networks. Theoretical guarantees are provided for pruning a single hidden layer fully connected network. Pruning with interpolative decompositions achieves strong empirical results compared to the state-of-the-art on multiple applications from one and two hidden layer networks on Fashion MNIST to VGG and ResNets on CIFAR-10. Notably, we achieve an accuracy of 93.62 $\pm$ 0.36% using VGG-16 on CIFAR-10, with a 51% FLOPS reduction. This gains 0.02% from the full-sized model.

The Fast Kernel Transform

Kernel methods are a highly effective and widely used collection of modern machine learning algorithms. A fundamental limitation of virtually all such methods are computations involving the kernel matrix that naively scale quadratically (e.g., constructing the kernel matrix and matrix-vector multiplication) or cubically (solving linear systems) with the size of the data set $N.$ We propose the Fast Kernel Transform (FKT), a general algorithm to compute matrix-vector multiplications (MVMs) for datasets in moderate dimensions with quasilinear complexity. Typically, analytically grounded fast multiplication methods require specialized development for specific kernels. In contrast, our scheme is based on auto-differentiation and automated symbolic computations that leverage the analytical structure of the underlying kernel. This allows the FKT to be easily applied to a broad class of kernels, including Gaussian, Matern, and Rational Quadratic covariance functions and physically motivated Green's functions, including those of the Laplace and Helmholtz equations. Furthermore, the FKT maintains a high, quantifiable, and controllable level of accuracy -- properties that many acceleration methods lack. We illustrate the efficacy and versatility of the FKT by providing timing and accuracy benchmarks and by applying it to scale the stochastic neighborhood embedding (t-SNE) and Gaussian processes to large real-world data sets.

Over-parametrized neural networks as under-determined linear systems

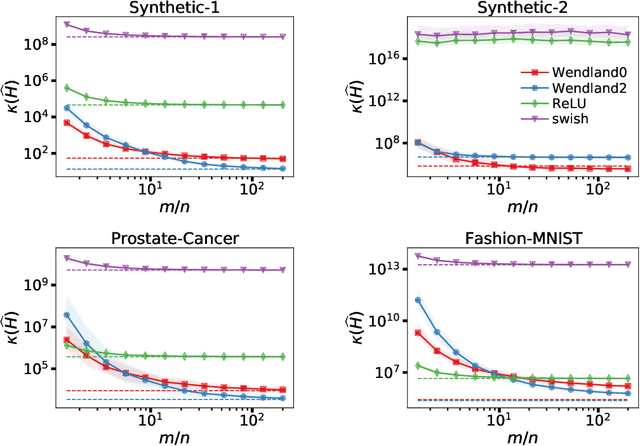
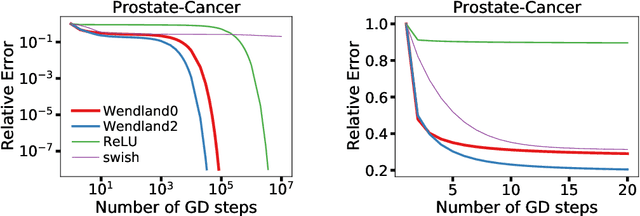
We draw connections between simple neural networks and under-determined linear systems to comprehensively explore several interesting theoretical questions in the study of neural networks. First, we emphatically show that it is unsurprising such networks can achieve zero training loss. More specifically, we provide lower bounds on the width of a single hidden layer neural network such that only training the last linear layer suffices to reach zero training loss. Our lower bounds grow more slowly with data set size than existing work that trains the hidden layer weights. Second, we show that kernels typically associated with the ReLU activation function have fundamental flaws -- there are simple data sets where it is impossible for widely studied bias-free models to achieve zero training loss irrespective of how the parameters are chosen or trained. Lastly, our analysis of gradient descent clearly illustrates how spectral properties of certain matrices impact both the early iteration and long-term training behavior. We propose new activation functions that avoid the pitfalls of ReLU in that they admit zero training loss solutions for any set of distinct data points and experimentally exhibit favorable spectral properties.

Communication-efficient distributed eigenspace estimation

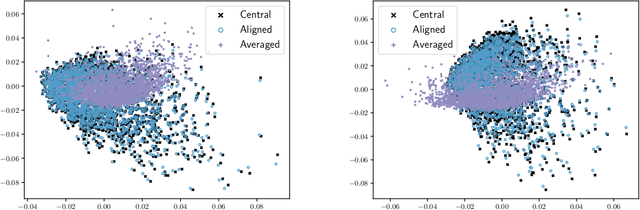
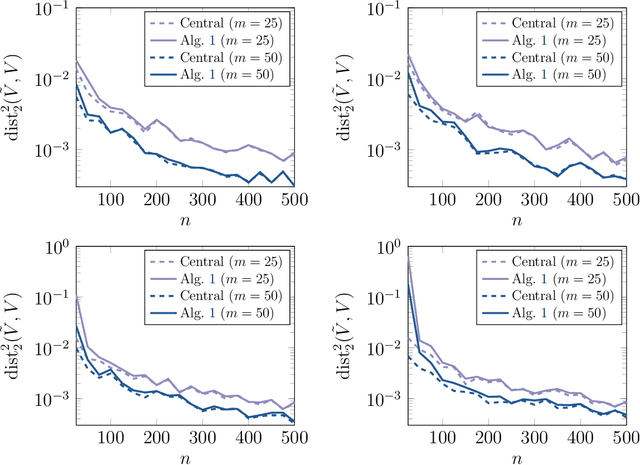
Distributed computing is a standard way to scale up machine learning and data science algorithms to process large amounts of data. In such settings, avoiding communication amongst machines is paramount for achieving high performance. Rather than distribute the computation of existing algorithms, a common practice for avoiding communication is to compute local solutions or parameter estimates on each machine and then combine the results; in many convex optimization problems, even simple averaging of local solutions can work well. However, these schemes do not work when the local solutions are not unique. Spectral methods are a collection of such problems, where solutions are orthonormal bases of the leading invariant subspace of an associated data matrix, which are only unique up to rotation and reflections. Here, we develop a communication-efficient distributed algorithm for computing the leading invariant subspace of a data matrix. Our algorithm uses a novel alignment scheme that minimizes the Procrustean distance between local solutions and a reference solution, and only requires a single round of communication. For the important case of principal component analysis (PCA), we show that our algorithm achieves a similar error rate to that of a centralized estimator. We present numerical experiments demonstrating the efficacy of our proposed algorithm for distributed PCA, as well as other problems where solutions exhibit rotational symmetry, such as node embeddings for graph data and spectral initialization for quadratic sensing.

Fast Matrix Square Roots with Applications to Gaussian Processes and Bayesian Optimization

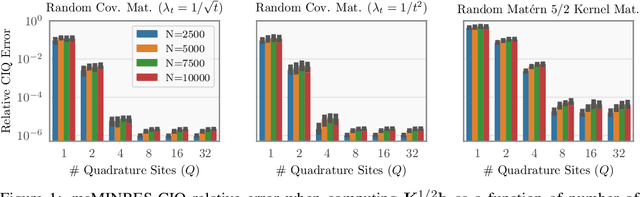
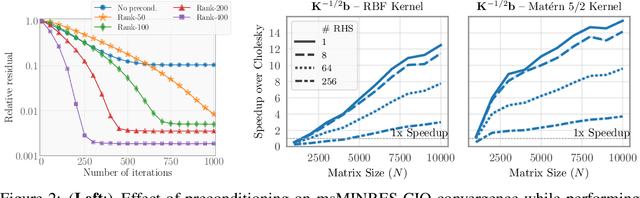
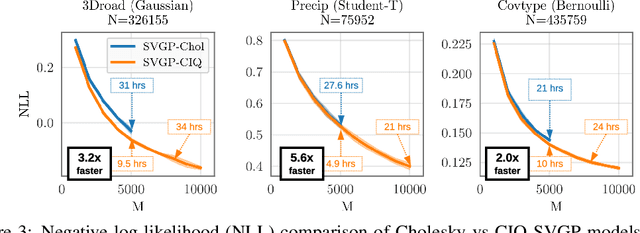
Matrix square roots and their inverses arise frequently in machine learning, e.g., when sampling from high-dimensional Gaussians $\mathcal{N}(\mathbf 0, \mathbf K)$ or whitening a vector $\mathbf b$ against covariance matrix $\mathbf K$. While existing methods typically require $O(N^3)$ computation, we introduce a highly-efficient quadratic-time algorithm for computing $\mathbf K^{1/2} \mathbf b$, $\mathbf K^{-1/2} \mathbf b$, and their derivatives through matrix-vector multiplication (MVMs). Our method combines Krylov subspace methods with a rational approximation and typically achieves $4$ decimal places of accuracy with fewer than $100$ MVMs. Moreover, the backward pass requires little additional computation. We demonstrate our method's applicability on matrices as large as $50,\!000 \times 50,\!000$ - well beyond traditional methods - with little approximation error. Applying this increased scalability to variational Gaussian processes, Bayesian optimization, and Gibbs sampling results in more powerful models with higher accuracy.

Entrywise convergence of iterative methods for eigenproblems

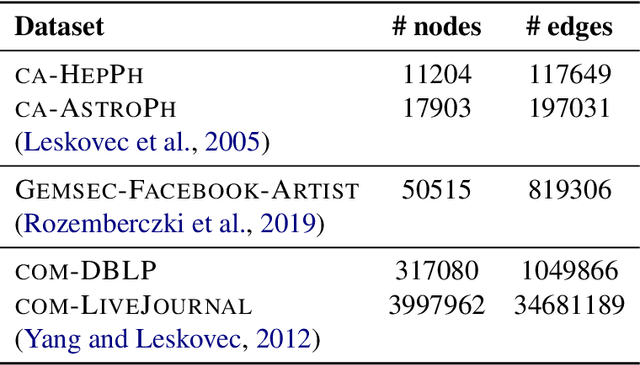
Several problems in machine learning, statistics, and other fields rely on computing eigenvectors. For large scale problems, the computation of these eigenvectors is typically performed via iterative schemes such as subspace iteration or Krylov methods. While there is classical and comprehensive analysis for subspace convergence guarantees with respect to the spectral norm, in many modern applications other notions of subspace distance are more appropriate. Recent theoretical work has focused on perturbations of subspaces measured in the $\ell_{2 \to \infty}$ norm, but does not consider the actual computation of eigenvectors. Here we address the convergence of subspace iteration when distances are measured in the $\ell_{2 \to \infty}$ norm and provide deterministic bounds. We complement our analysis with a practical stopping criterion and demonstrate its applicability via numerical experiments. Our results show that one can get comparable performance on downstream tasks while requiring fewer iterations, thereby saving substantial computational time.