Understanding Non-linearity in Graph Neural Networks from the Bayesian-Inference Perspective

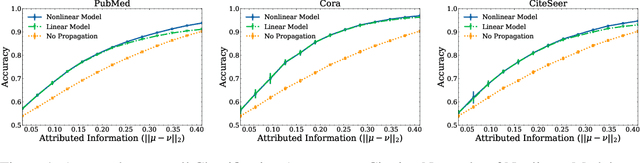
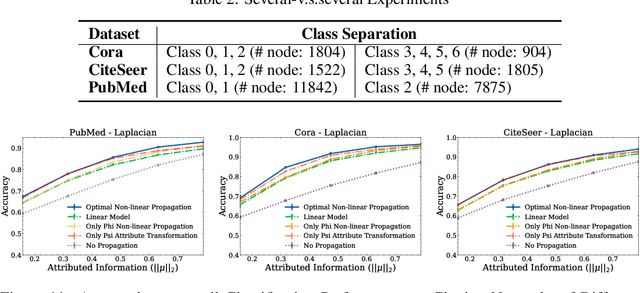
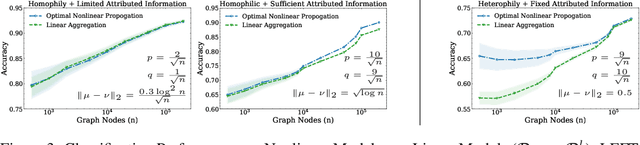
Graph neural networks (GNNs) have shown superiority in many prediction tasks over graphs due to their impressive capability of capturing nonlinear relations in graph-structured data. However, for node classification tasks, often, only marginal improvement of GNNs over their linear counterparts has been observed. Previous works provide very few understandings of this phenomenon. In this work, we resort to Bayesian learning to deeply investigate the functions of non-linearity in GNNs for node classification tasks. Given a graph generated from the statistical model CSBM, we observe that the max-a-posterior estimation of a node label given its own and neighbors' attributes consists of two types of non-linearity, a possibly non-linear transformation of node attributes and a ReLU-activated feature aggregation from neighbors. The latter surprisingly matches the type of non-linearity used in many GNN models. By further imposing Gaussian assumption on node attributes, we prove that the superiority of those ReLU activations is only significant when the node attributes are far more informative than the graph structure, which nicely matches many previous empirical observations. A similar argument can be achieved when there is a distribution shift of node attributes between the training and testing datasets. Finally, we verify our theory on both synthetic and real-world networks.

Graph-Based Methods for Discrete Choice

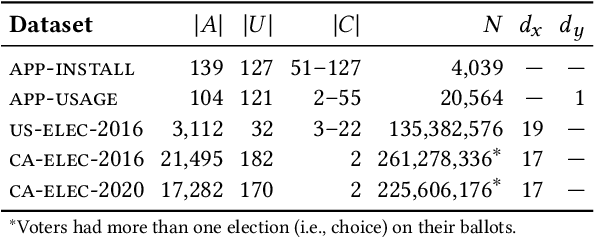
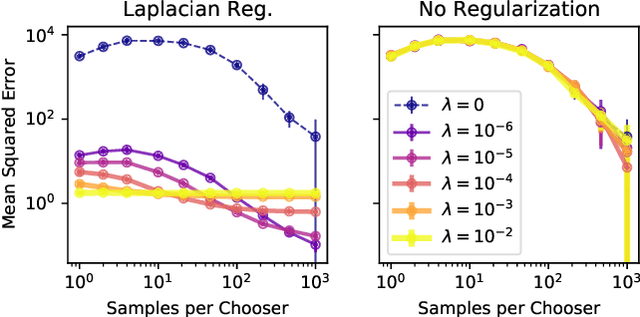
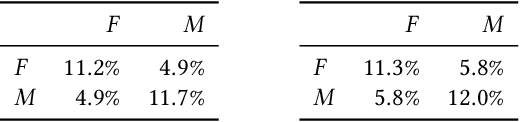
Choices made by individuals have widespread impacts--for instance, people choose between political candidates to vote for, between social media posts to share, and between brands to purchase--moreover, data on these choices are increasingly abundant. Discrete choice models are a key tool for learning individual preferences from such data. Additionally, social factors like conformity and contagion influence individual choice. Existing methods for incorporating these factors into choice models do not account for the entire social network and require hand-crafted features. To overcome these limitations, we use graph learning to study choice in networked contexts. We identify three ways in which graph learning techniques can be used for discrete choice: learning chooser representations, regularizing choice model parameters, and directly constructing predictions from a network. We design methods in each category and test them on real-world choice datasets, including county-level 2016 US election results and Android app installation and usage data. We show that incorporating social network structure can improve the predictions of the standard econometric choice model, the multinomial logit. We provide evidence that app installations are influenced by social context, but we find no such effect on app usage among the same participants, which instead is habit-driven. In the election data, we highlight the additional insights a discrete choice framework provides over classification or regression, the typical approaches. On synthetic data, we demonstrate the sample complexity benefit of using social information in choice models.

Approximate Decomposable Submodular Function Minimization for Cardinality-Based Components

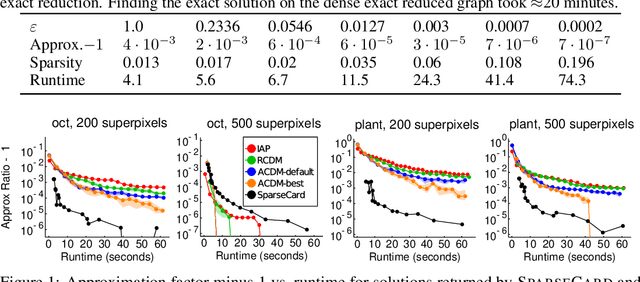
Minimizing a sum of simple submodular functions of limited support is a special case of general submodular function minimization that has seen numerous applications in machine learning. We develop fast techniques for instances where components in the sum are cardinality-based, meaning they depend only on the size of the input set. This variant is one of the most widely applied in practice, encompassing, e.g., common energy functions arising in image segmentation and recent generalized hypergraph cut functions. We develop the first approximation algorithms for this problem, where the approximations can be quickly computed via reduction to a sparse graph cut problem, with graph sparsity controlled by the desired approximation factor. Our method relies on a new connection between sparse graph reduction techniques and piecewise linear approximations to concave functions. Our sparse reduction technique leads to significant improvements in theoretical runtimes, as well as substantial practical gains in problems ranging from benchmark image segmentation tasks to hypergraph clustering problems.

Edge Proposal Sets for Link Prediction

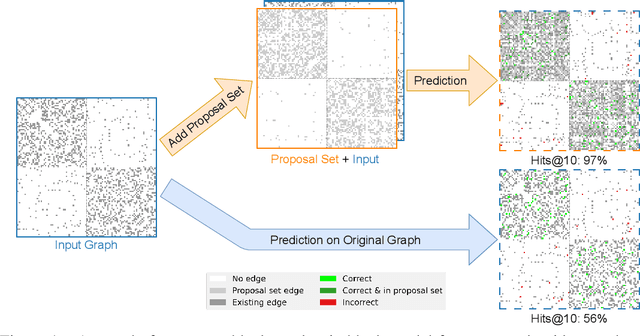
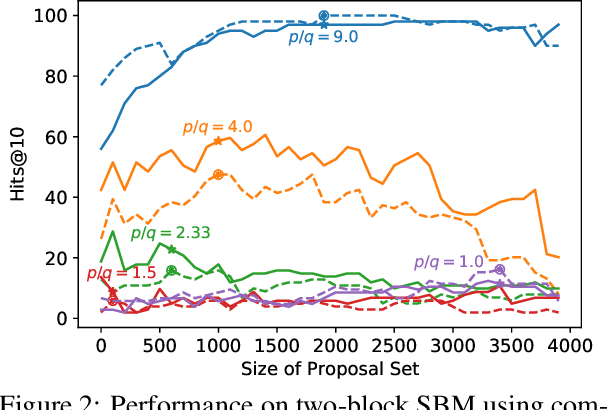
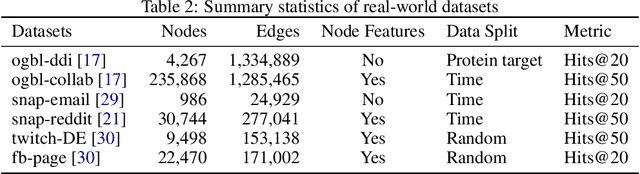
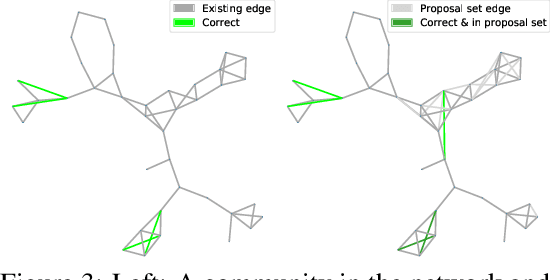
Graphs are a common model for complex relational data such as social networks and protein interactions, and such data can evolve over time (e.g., new friendships) and be noisy (e.g., unmeasured interactions). Link prediction aims to predict future edges or infer missing edges in the graph, and has diverse applications in recommender systems, experimental design, and complex systems. Even though link prediction algorithms strongly depend on the set of edges in the graph, existing approaches typically do not modify the graph topology to improve performance. Here, we demonstrate how simply adding a set of edges, which we call a \emph{proposal set}, to the graph as a pre-processing step can improve the performance of several link prediction algorithms. The underlying idea is that if the edges in the proposal set generally align with the structure of the graph, link prediction algorithms are further guided towards predicting the right edges; in other words, adding a proposal set of edges is a signal-boosting pre-processing step. We show how to use existing link prediction algorithms to generate effective proposal sets and evaluate this approach on various synthetic and empirical datasets. We find that proposal sets meaningfully improve the accuracy of link prediction algorithms based on both neighborhood heuristics and graph neural networks. Code is available at \url{https://github.com/CUAI/Edge-Proposal-Sets}.

Graph Belief Propagation Networks

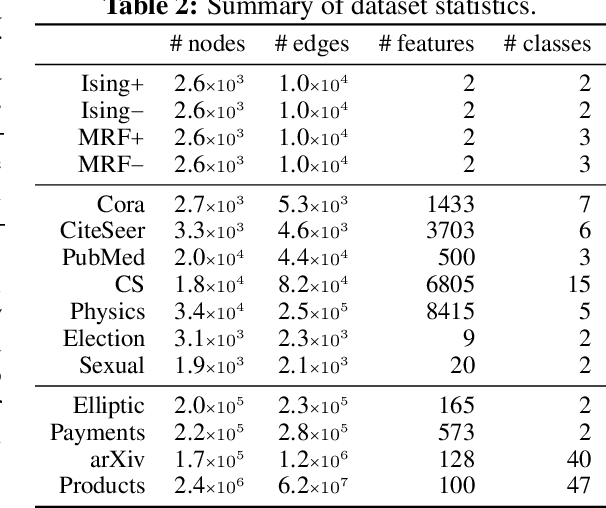
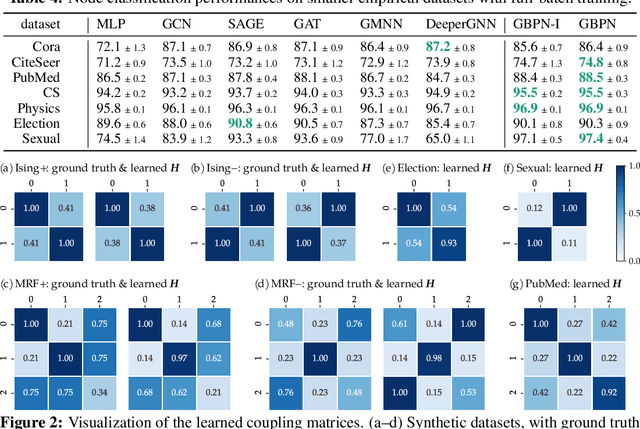
With the wide-spread availability of complex relational data, semi-supervised node classification in graphs has become a central machine learning problem. Graph neural networks are a recent class of easy-to-train and accurate methods for this problem that map the features in the neighborhood of a node to its label, but they ignore label correlation during inference and their predictions are difficult to interpret. On the other hand, collective classification is a traditional approach based on interpretable graphical models that explicitly model label correlations. Here, we introduce a model that combines the advantages of these two approaches, where we compute the marginal probabilities in a conditional random field, similar to collective classification, and the potentials in the random field are learned through end-to-end training, akin to graph neural networks. In our model, potentials on each node only depend on that node's features, and edge potentials are learned via a coupling matrix. This structure enables simple training with interpretable parameters, scales to large networks, naturally incorporates training labels at inference, and is often more accurate than related approaches. Our approach can be viewed as either an interpretable message-passing graph neural network or a collective classification method with higher capacity and modernized training.

The Generalized Mean Densest Subgraph Problem

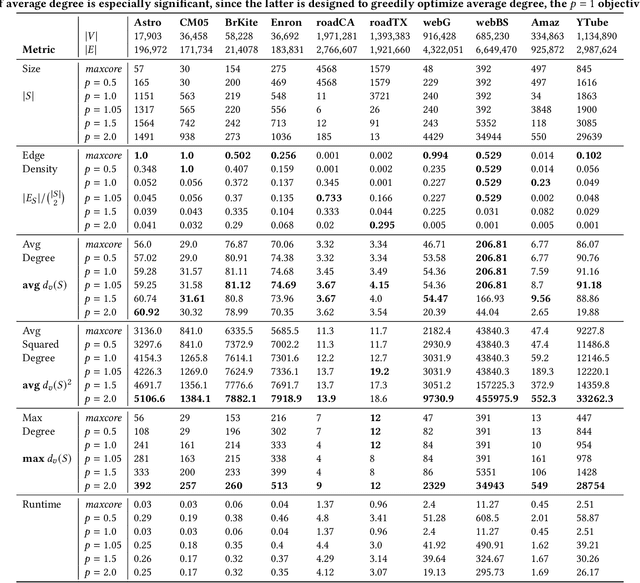
Finding dense subgraphs of a large graph is a standard problem in graph mining that has been studied extensively both for its theoretical richness and its many practical applications. In this paper we introduce a new family of dense subgraph objectives, parameterized by a single parameter $p$, based on computing generalized means of degree sequences of a subgraph. Our objective captures both the standard densest subgraph problem and the maximum $k$-core as special cases, and provides a way to interpolate between and extrapolate beyond these two objectives when searching for other notions of dense subgraphs. In terms of algorithmic contributions, we first show that our objective can be minimized in polynomial time for all $p \geq 1$ using repeated submodular minimization. A major contribution of our work is analyzing the performance of different types of peeling algorithms for dense subgraphs both in theory and practice. We prove that the standard peeling algorithm can perform arbitrarily poorly on our generalized objective, but we then design a more sophisticated peeling method which for $p \geq 1$ has an approximation guarantee that is always at least $1/2$ and converges to 1 as $p \rightarrow \infty$. In practice, we show that this algorithm obtains extremely good approximations to the optimal solution, scales to large graphs, and highlights a range of different meaningful notions of density on graphs coming from numerous domains. Furthermore, it is typically able to approximate the densest subgraph problem better than the standard peeling algorithm, by better accounting for how the removal of one node affects other nodes in its neighborhood.

Choice Set Confounding in Discrete Choice

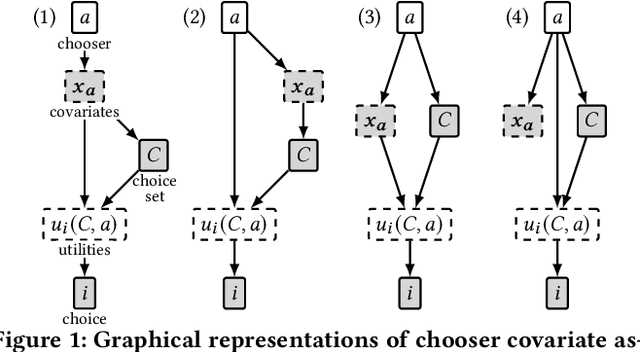
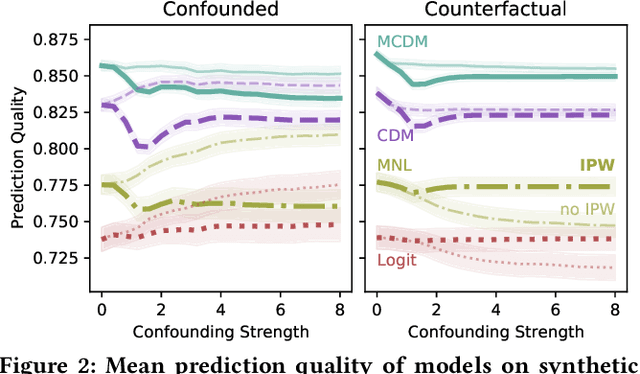
Standard methods in preference learning involve estimating the parameters of discrete choice models from data of selections (choices) made by individuals from a discrete set of alternatives (the choice set). While there are many models for individual preferences, existing learning methods overlook how choice set assignment affects the data. Often, the choice set itself is influenced by an individual's preferences; for instance, a consumer choosing a product from an online retailer is often presented with options from a recommender system that depend on information about the consumer's preferences. Ignoring these assignment mechanisms can mislead choice models into making biased estimates of preferences, a phenomenon that we call choice set confounding; we demonstrate the presence of such confounding in widely-used choice datasets. To address this issue, we adapt methods from causal inference to the discrete choice setting. We use covariates of the chooser for inverse probability weighting and/or regression controls, accurately recovering individual preferences in the presence of choice set confounding under certain assumptions. When such covariates are unavailable or inadequate, we develop methods that take advantage of structured choice set assignment to improve prediction. We demonstrate the effectiveness of our methods on real-world choice data, showing, for example, that accounting for choice set confounding makes choices observed in hotel booking and commute transportation more consistent with rational utility-maximization.

A nonlinear diffusion method for semi-supervised learning on hypergraphs

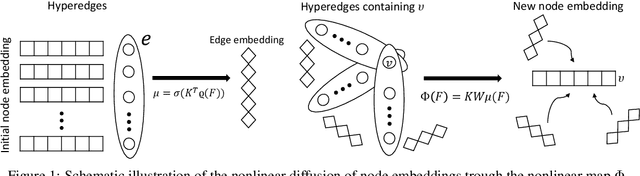
Hypergraphs are a common model for multiway relationships in data, and hypergraph semi-supervised learning is the problem of assigning labels to all nodes in a hypergraph, given labels on just a few nodes. Diffusions and label spreading are classical techniques for semi-supervised learning in the graph setting, and there are some standard ways to extend them to hypergraphs. However, these methods are linear models, and do not offer an obvious way of incorporating node features for making predictions. Here, we develop a nonlinear diffusion process on hypergraphs that spreads both features and labels following the hypergraph structure, which can be interpreted as a hypergraph equilibrium network. Even though the process is nonlinear, we show global convergence to a unique limiting point for a broad class of nonlinearities, which is the global optimum of a interpretable, regularized semi-supervised learning loss function. The limiting point serves as a node embedding from which we make predictions with a linear model. Our approach is much more accurate than several hypergraph neural networks, and also takes less time to train.

A Unifying Generative Model for Graph Learning Algorithms: Label Propagation, Graph Convolutions, and Combinations

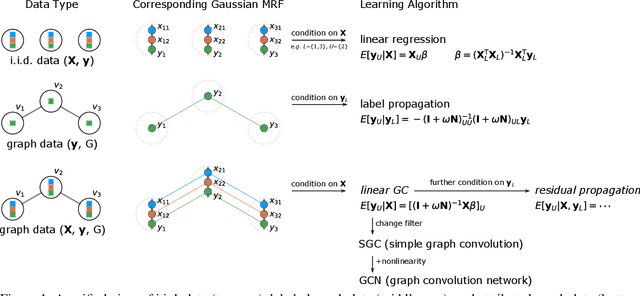
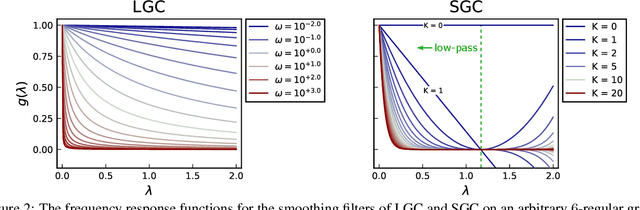
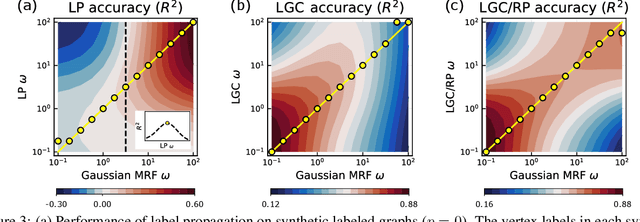
Semi-supervised learning on graphs is a widely applicable problem in network science and machine learning. Two standard algorithms -- label propagation and graph neural networks -- both operate by repeatedly passing information along edges, the former by passing labels and the latter by passing node features, modulated by neural networks. These two types of algorithms have largely developed separately, and there is little understanding about the structure of network data that would make one of these approaches work particularly well compared to the other or when the approaches can be meaningfully combined. Here, we develop a Markov random field model for the data generation process of node attributes, based on correlations of attributes on and between vertices, that motivates and unifies these algorithmic approaches. We show that label propagation, a linearized graph convolutional network, and their combination can all be derived as conditional expectations under our model, when conditioning on different attributes. In addition, the data model highlights deficiencies in existing graph neural networks (while producing new algorithmic solutions), serves as a rigorous statistical framework for understanding graph learning issues such as over-smoothing, creates a testbed for evaluating inductive learning performance, and provides a way to sample graphs attributes that resemble empirical data. We also find that a new algorithm derived from our data generation model, which we call a Linear Graph Convolution, performs extremely well in practice on empirical data, and provide theoretical justification for why this is the case.

Generative hypergraph clustering: from blockmodels to modularity

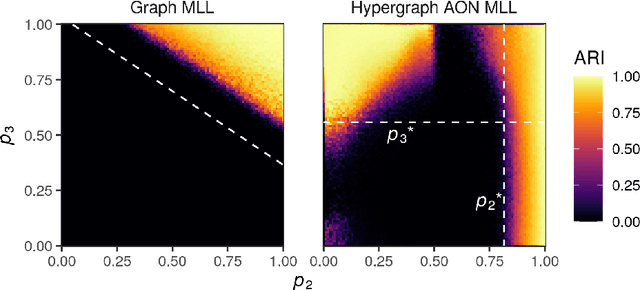
Hypergraphs are a natural modeling paradigm for a wide range of complex relational systems with multibody interactions. A standard analysis task is to identify clusters of closely related or densely interconnected nodes. While many probabilistic generative models for graph clustering have been proposed, there are relatively few such models for hypergraphs. We propose a Poisson degree-corrected hypergraph stochastic blockmodel (DCHSBM), an expressive generative model of clustered hypergraphs with heterogeneous node degrees and edge sizes. Approximate maximum-likelihood inference in the DCHSBM naturally leads to a clustering objective that generalizes the popular modularity objective for graphs. We derive a general Louvain-type algorithm for this objective, as well as a a faster, specialized "All-Or-Nothing" (AON) variant in which edges are expected to lie fully within clusters. This special case encompasses a recent proposal for modularity in hypergraphs, while also incorporating flexible resolution and edge-size parameters. We show that hypergraph Louvain is highly scalable, including as an example an experiment on a synthetic hypergraph of one million nodes. We also demonstrate through synthetic experiments that the detectability regimes for hypergraph community detection differ from methods based on dyadic graph projections. In particular, there are regimes in which hypergraph methods can recover planted partitions even though graph based methods necessarily fail due to information-theoretic limits. We use our model to analyze different patterns of higher-order structure in school contact networks, U.S. congressional bill cosponsorship, U.S. congressional committees, product categories in co-purchasing behavior, and hotel locations from web browsing sessions, that it is able to recover ground truth clusters in empirical data sets exhibiting the corresponding higher-order structure.