A Unifying Generative Model for Graph Learning Algorithms: Label Propagation, Graph Convolutions, and Combinations
Paper and Code
Jan 30, 2021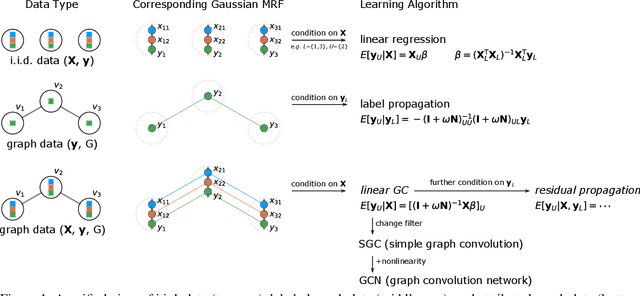

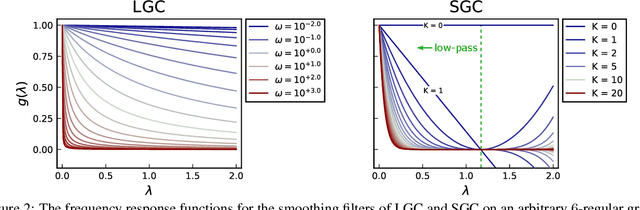
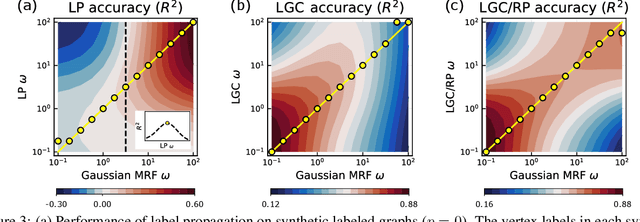
Semi-supervised learning on graphs is a widely applicable problem in network science and machine learning. Two standard algorithms -- label propagation and graph neural networks -- both operate by repeatedly passing information along edges, the former by passing labels and the latter by passing node features, modulated by neural networks. These two types of algorithms have largely developed separately, and there is little understanding about the structure of network data that would make one of these approaches work particularly well compared to the other or when the approaches can be meaningfully combined. Here, we develop a Markov random field model for the data generation process of node attributes, based on correlations of attributes on and between vertices, that motivates and unifies these algorithmic approaches. We show that label propagation, a linearized graph convolutional network, and their combination can all be derived as conditional expectations under our model, when conditioning on different attributes. In addition, the data model highlights deficiencies in existing graph neural networks (while producing new algorithmic solutions), serves as a rigorous statistical framework for understanding graph learning issues such as over-smoothing, creates a testbed for evaluating inductive learning performance, and provides a way to sample graphs attributes that resemble empirical data. We also find that a new algorithm derived from our data generation model, which we call a Linear Graph Convolution, performs extremely well in practice on empirical data, and provide theoretical justification for why this is the case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge