Generative hypergraph clustering: from blockmodels to modularity
Paper and Code
Jan 27, 2021

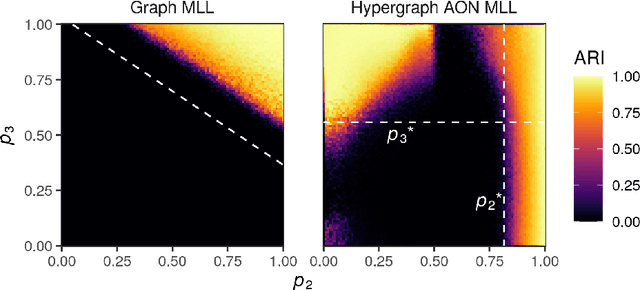

Hypergraphs are a natural modeling paradigm for a wide range of complex relational systems with multibody interactions. A standard analysis task is to identify clusters of closely related or densely interconnected nodes. While many probabilistic generative models for graph clustering have been proposed, there are relatively few such models for hypergraphs. We propose a Poisson degree-corrected hypergraph stochastic blockmodel (DCHSBM), an expressive generative model of clustered hypergraphs with heterogeneous node degrees and edge sizes. Approximate maximum-likelihood inference in the DCHSBM naturally leads to a clustering objective that generalizes the popular modularity objective for graphs. We derive a general Louvain-type algorithm for this objective, as well as a a faster, specialized "All-Or-Nothing" (AON) variant in which edges are expected to lie fully within clusters. This special case encompasses a recent proposal for modularity in hypergraphs, while also incorporating flexible resolution and edge-size parameters. We show that hypergraph Louvain is highly scalable, including as an example an experiment on a synthetic hypergraph of one million nodes. We also demonstrate through synthetic experiments that the detectability regimes for hypergraph community detection differ from methods based on dyadic graph projections. In particular, there are regimes in which hypergraph methods can recover planted partitions even though graph based methods necessarily fail due to information-theoretic limits. We use our model to analyze different patterns of higher-order structure in school contact networks, U.S. congressional bill cosponsorship, U.S. congressional committees, product categories in co-purchasing behavior, and hotel locations from web browsing sessions, that it is able to recover ground truth clusters in empirical data sets exhibiting the corresponding higher-order structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge