Edge-Colored Clustering in Hypergraphs: Beyond Minimizing Unsatisfied Edges

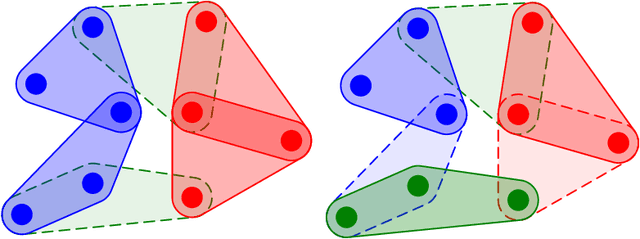
We consider a framework for clustering edge-colored hypergraphs, where the goal is to cluster (equivalently, to color) objects based on the primary type of multiway interactions they participate in. One well-studied objective is to color nodes to minimize the number of unsatisfied hyperedges -- those containing one or more nodes whose color does not match the hyperedge color. We motivate and present advances for several directions that extend beyond this minimization problem. We first provide new algorithms for maximizing satisfied edges, which is the same at optimality but is much more challenging to approximate, with all prior work restricted to graphs. We develop the first approximation algorithm for hypergraphs, and then refine it to improve the best-known approximation factor for graphs. We then introduce new objective functions that incorporate notions of balance and fairness, and provide new hardness results, approximations, and fixed-parameter tractability results.

Approximate Tree Completion and Learning-Augmented Algorithms for Metric Minimum Spanning Trees

Finding a minimum spanning tree (MST) for $n$ points in an arbitrary metric space is a fundamental primitive for hierarchical clustering and many other ML tasks, but this takes $\Omega(n^2)$ time to even approximate. We introduce a framework for metric MSTs that first (1) finds a forest of disconnected components using practical heuristics, and then (2) finds a small weight set of edges to connect disjoint components of the forest into a spanning tree. We prove that optimally solving the second step still takes $\Omega(n^2)$ time, but we provide a subquadratic 2.62-approximation algorithm. In the spirit of learning-augmented algorithms, we then show that if the forest found in step (1) overlaps with an optimal MST, we can approximate the original MST problem in subquadratic time, where the approximation factor depends on a measure of overlap. In practice, we find nearly optimal spanning trees for a wide range of metrics, while being orders of magnitude faster than exact algorithms.

Combinatorial Approximations for Cluster Deletion: Simpler, Faster, and Better

Cluster deletion is an NP-hard graph clustering objective with applications in computational biology and social network analysis, where the goal is to delete a minimum number of edges to partition a graph into cliques. We first provide a tighter analysis of two previous approximation algorithms, improving their approximation guarantees from 4 to 3. Moreover, we show that both algorithms can be derandomized in a surprisingly simple way, by greedily taking a vertex of maximum degree in an auxiliary graph and forming a cluster around it. One of these algorithms relies on solving a linear program. Our final contribution is to design a new and purely combinatorial approach for doing so that is far more scalable in theory and practice.

Faster Approximation Algorithms for Parameterized Graph Clustering and Edge Labeling

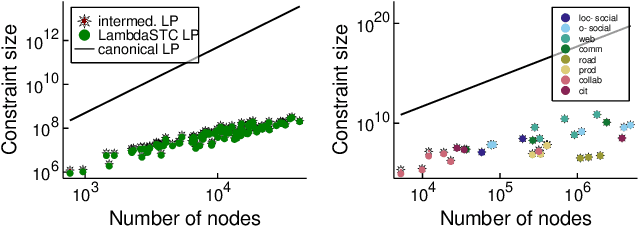
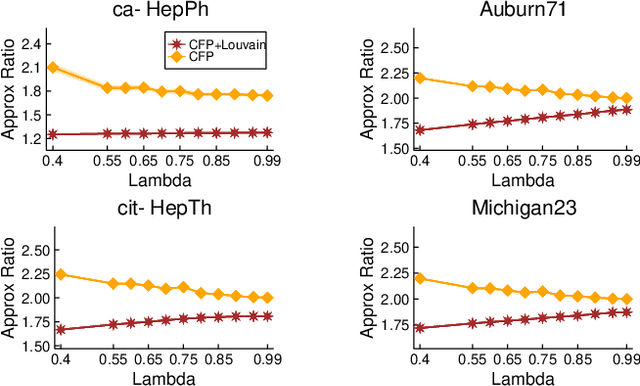
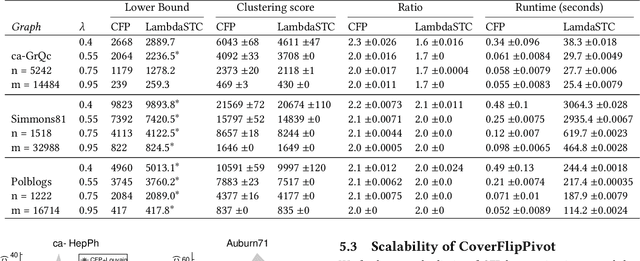
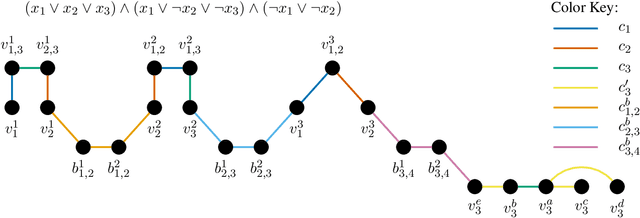
Graph clustering is a fundamental task in network analysis where the goal is to detect sets of nodes that are well-connected to each other but sparsely connected to the rest of the graph. We present faster approximation algorithms for an NP-hard parameterized clustering framework called LambdaCC, which is governed by a tunable resolution parameter and generalizes many other clustering objectives such as modularity, sparsest cut, and cluster deletion. Previous LambdaCC algorithms are either heuristics with no approximation guarantees, or computationally expensive approximation algorithms. We provide fast new approximation algorithms that can be made purely combinatorial. These rely on a new parameterized edge labeling problem we introduce that generalizes previous edge labeling problems that are based on the principle of strong triadic closure and are of independent interest in social network analysis. Our methods are orders of magnitude more scalable than previous approximation algorithms and our lower bounds allow us to obtain a posteriori approximation guarantees for previous heuristics that have no approximation guarantees of their own.

On the Optimal Recovery of Graph Signals

Learning a smooth graph signal from partially observed data is a well-studied task in graph-based machine learning. We consider this task from the perspective of optimal recovery, a mathematical framework for learning a function from observational data that adopts a worst-case perspective tied to model assumptions on the function to be learned. Earlier work in the optimal recovery literature has shown that minimizing a regularized objective produces optimal solutions for a general class of problems, but did not fully identify the regularization parameter. Our main contribution provides a way to compute regularization parameters that are optimal or near-optimal (depending on the setting), specifically for graph signal processing problems. Our results offer a new interpretation for classical optimization techniques in graph-based learning and also come with new insights for hyperparameter selection. We illustrate the potential of our methods in numerical experiments on several semi-synthetic graph signal processing datasets.

Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

Faster Deterministic Approximation Algorithms for Correlation Clustering and Cluster Deletion

Correlation clustering is a framework for partitioning datasets based on pairwise similarity and dissimilarity scores, and has been used for diverse applications in bioinformatics, social network analysis, and computer vision. Although many approximation algorithms have been designed for this problem, the best theoretical results rely on obtaining lower bounds via expensive linear programming relaxations. In this paper we prove new relationships between correlation clustering problems and edge labeling problems related to the principle of strong triadic closure. We use these connections to develop new approximation algorithms for correlation clustering that have deterministic constant factor approximation guarantees and avoid the canonical linear programming relaxation. Our approach also extends to a variant of correlation clustering called cluster deletion, that strictly prohibits placing negative edges inside clusters. Our results include 4-approximation algorithms for cluster deletion and correlation clustering, based on simplified linear programs with far fewer constraints than the canonical relaxations. More importantly, we develop faster techniques that are purely combinatorial, based on computing maximal matchings in certain auxiliary graphs and hypergraphs. This leads to a combinatorial 6-approximation for complete unweighted correlation clustering, which is the best deterministic result for any method that does not rely on linear programming. We also present the first combinatorial constant factor approximation for cluster deletion.

Approximate Decomposable Submodular Function Minimization for Cardinality-Based Components

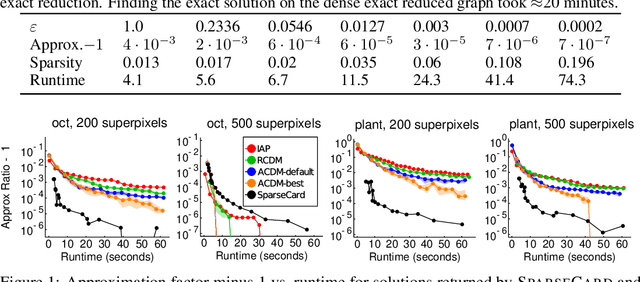
Minimizing a sum of simple submodular functions of limited support is a special case of general submodular function minimization that has seen numerous applications in machine learning. We develop fast techniques for instances where components in the sum are cardinality-based, meaning they depend only on the size of the input set. This variant is one of the most widely applied in practice, encompassing, e.g., common energy functions arising in image segmentation and recent generalized hypergraph cut functions. We develop the first approximation algorithms for this problem, where the approximations can be quickly computed via reduction to a sparse graph cut problem, with graph sparsity controlled by the desired approximation factor. Our method relies on a new connection between sparse graph reduction techniques and piecewise linear approximations to concave functions. Our sparse reduction technique leads to significant improvements in theoretical runtimes, as well as substantial practical gains in problems ranging from benchmark image segmentation tasks to hypergraph clustering problems.

The Generalized Mean Densest Subgraph Problem

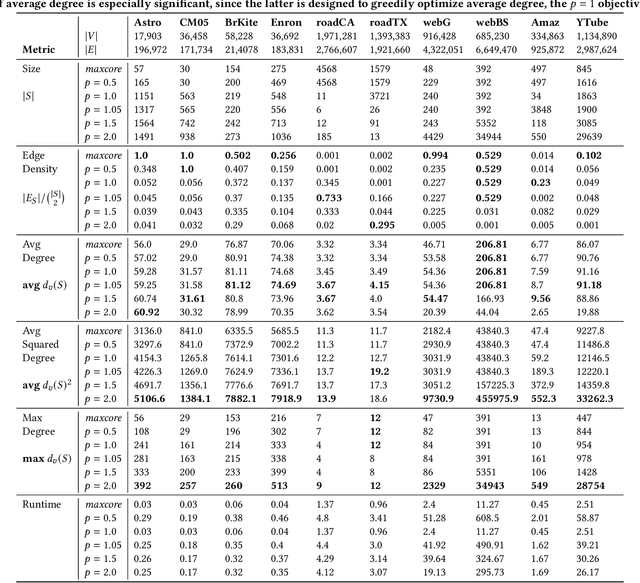
Finding dense subgraphs of a large graph is a standard problem in graph mining that has been studied extensively both for its theoretical richness and its many practical applications. In this paper we introduce a new family of dense subgraph objectives, parameterized by a single parameter $p$, based on computing generalized means of degree sequences of a subgraph. Our objective captures both the standard densest subgraph problem and the maximum $k$-core as special cases, and provides a way to interpolate between and extrapolate beyond these two objectives when searching for other notions of dense subgraphs. In terms of algorithmic contributions, we first show that our objective can be minimized in polynomial time for all $p \geq 1$ using repeated submodular minimization. A major contribution of our work is analyzing the performance of different types of peeling algorithms for dense subgraphs both in theory and practice. We prove that the standard peeling algorithm can perform arbitrarily poorly on our generalized objective, but we then design a more sophisticated peeling method which for $p \geq 1$ has an approximation guarantee that is always at least $1/2$ and converges to 1 as $p \rightarrow \infty$. In practice, we show that this algorithm obtains extremely good approximations to the optimal solution, scales to large graphs, and highlights a range of different meaningful notions of density on graphs coming from numerous domains. Furthermore, it is typically able to approximate the densest subgraph problem better than the standard peeling algorithm, by better accounting for how the removal of one node affects other nodes in its neighborhood.

Generative hypergraph clustering: from blockmodels to modularity

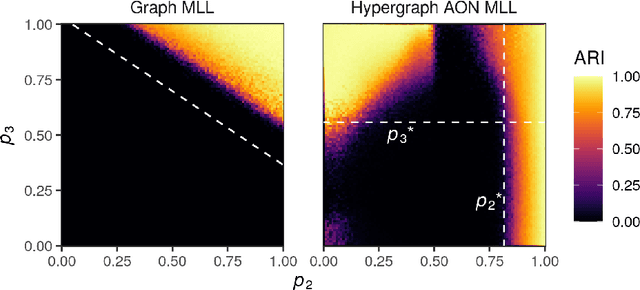
Hypergraphs are a natural modeling paradigm for a wide range of complex relational systems with multibody interactions. A standard analysis task is to identify clusters of closely related or densely interconnected nodes. While many probabilistic generative models for graph clustering have been proposed, there are relatively few such models for hypergraphs. We propose a Poisson degree-corrected hypergraph stochastic blockmodel (DCHSBM), an expressive generative model of clustered hypergraphs with heterogeneous node degrees and edge sizes. Approximate maximum-likelihood inference in the DCHSBM naturally leads to a clustering objective that generalizes the popular modularity objective for graphs. We derive a general Louvain-type algorithm for this objective, as well as a a faster, specialized "All-Or-Nothing" (AON) variant in which edges are expected to lie fully within clusters. This special case encompasses a recent proposal for modularity in hypergraphs, while also incorporating flexible resolution and edge-size parameters. We show that hypergraph Louvain is highly scalable, including as an example an experiment on a synthetic hypergraph of one million nodes. We also demonstrate through synthetic experiments that the detectability regimes for hypergraph community detection differ from methods based on dyadic graph projections. In particular, there are regimes in which hypergraph methods can recover planted partitions even though graph based methods necessarily fail due to information-theoretic limits. We use our model to analyze different patterns of higher-order structure in school contact networks, U.S. congressional bill cosponsorship, U.S. congressional committees, product categories in co-purchasing behavior, and hotel locations from web browsing sessions, that it is able to recover ground truth clusters in empirical data sets exhibiting the corresponding higher-order structure.