Discovering Global False Negatives On the Fly for Self-supervised Contrastive Learning

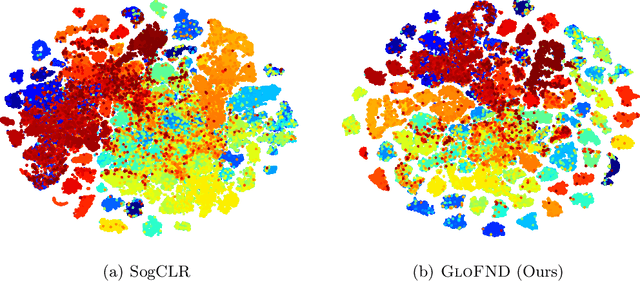
In self-supervised contrastive learning, negative pairs are typically constructed using an anchor image and a sample drawn from the entire dataset, excluding the anchor. However, this approach can result in the creation of negative pairs with similar semantics, referred to as "false negatives", leading to their embeddings being falsely pushed apart. To address this issue, we introduce GloFND, an optimization-based approach that automatically learns on the fly the threshold for each anchor data to identify its false negatives during training. In contrast to previous methods for false negative discovery, our approach globally detects false negatives across the entire dataset rather than locally within the mini-batch. Moreover, its per-iteration computation cost remains independent of the dataset size. Experimental results on image and image-text data demonstrate the effectiveness of the proposed method. Our implementation is available at https://github.com/vibalcam/GloFND .

Discriminative Finetuning of Generative Large Language Models without Reward Models and Preference Data

Supervised fine-tuning (SFT) followed by preference optimization (PO) denoted by SFT$\rightarrow$PO has become the standard for improving pretrained large language models (LLMs), with PO demonstrating significant performance gains. However, PO methods rely on either human-labeled preference data or a strong reward model to generate preference data. Can we fine-tune LLMs without preference data or reward models while achieving competitive performance to SFT$\rightarrow$PO? We address this question by introducing Discriminative Fine-Tuning (DFT), a novel approach that eliminates the need for preference data. Unlike SFT, which employs a generative approach and overlooks negative data, DFT adopts a discriminative paradigm that that increases the probability of positive answers while suppressing potentially negative ones, shifting from token prediction to data prediction. Our contributions include: (i) a discriminative probabilistic framework for fine-tuning LLMs by explicitly modeling the discriminative likelihood of an answer among all possible outputs given an input; (ii) efficient algorithms to optimize this discriminative likelihood; and (iii) extensive experiments demonstrating DFT's effectiveness, achieving performance better than SFT and comparable to if not better than SFT$\rightarrow$PO. The code can be found at https://github.com/PenGuln/DFT.

Combinatorial Approximations for Cluster Deletion: Simpler, Faster, and Better

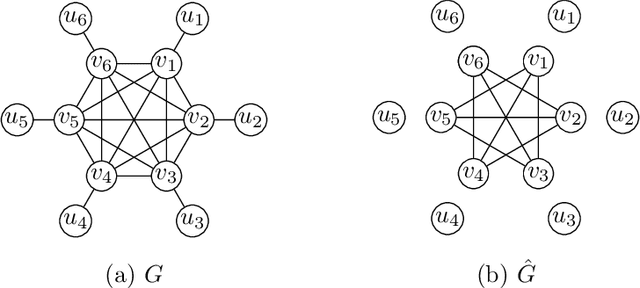
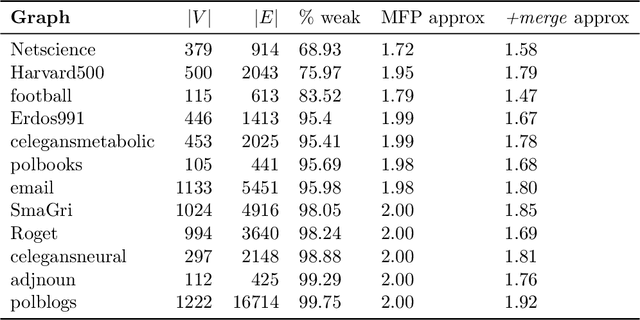
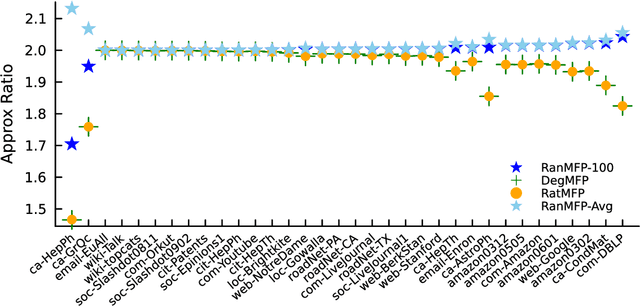
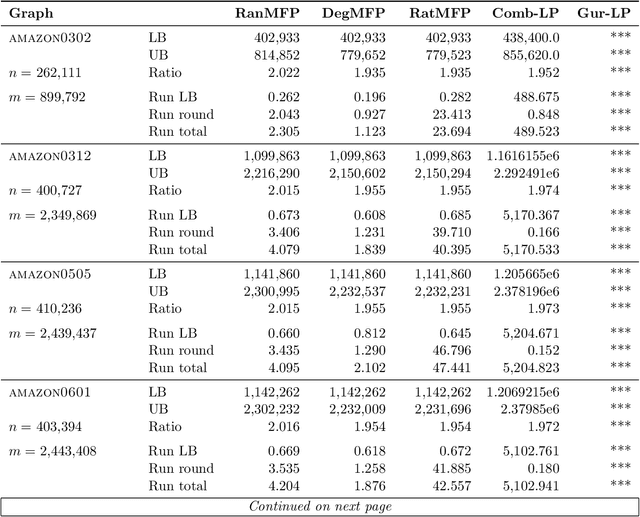
Cluster deletion is an NP-hard graph clustering objective with applications in computational biology and social network analysis, where the goal is to delete a minimum number of edges to partition a graph into cliques. We first provide a tighter analysis of two previous approximation algorithms, improving their approximation guarantees from 4 to 3. Moreover, we show that both algorithms can be derandomized in a surprisingly simple way, by greedily taking a vertex of maximum degree in an auxiliary graph and forming a cluster around it. One of these algorithms relies on solving a linear program. Our final contribution is to design a new and purely combinatorial approach for doing so that is far more scalable in theory and practice.