Bokun Wang
Stochastic Primal-Dual Double Block-Coordinate for Two-way Partial AUC Maximization
May 28, 2025Abstract:Two-way partial AUC (TPAUC) is a critical performance metric for binary classification with imbalanced data, as it focuses on specific ranges of the true positive rate (TPR) and false positive rate (FPR). However, stochastic algorithms for TPAUC optimization remain under-explored, with existing methods either limited to approximated TPAUC loss functions or burdened by sub-optimal complexities. To overcome these limitations, we introduce two innovative stochastic primal-dual double block-coordinate algorithms for TPAUC maximization. These algorithms utilize stochastic block-coordinate updates for both the primal and dual variables, catering to both convex and non-convex settings. We provide theoretical convergence rate analyses, demonstrating significant improvements over prior approaches. Our experimental results, based on multiple benchmark datasets, validate the superior performance of our algorithms, showcasing faster convergence and better generalization. This work advances the state of the art in TPAUC optimization and offers practical tools for real-world machine learning applications.
Discovering Global False Negatives On the Fly for Self-supervised Contrastive Learning
Feb 28, 2025

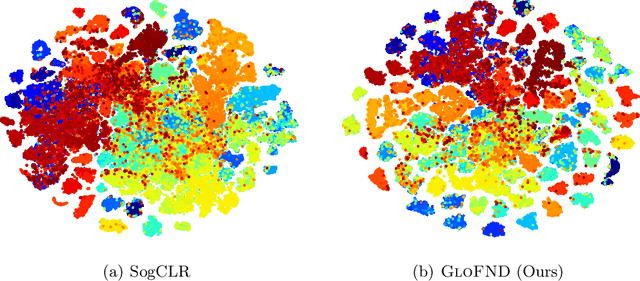

Abstract:In self-supervised contrastive learning, negative pairs are typically constructed using an anchor image and a sample drawn from the entire dataset, excluding the anchor. However, this approach can result in the creation of negative pairs with similar semantics, referred to as "false negatives", leading to their embeddings being falsely pushed apart. To address this issue, we introduce GloFND, an optimization-based approach that automatically learns on the fly the threshold for each anchor data to identify its false negatives during training. In contrast to previous methods for false negative discovery, our approach globally detects false negatives across the entire dataset rather than locally within the mini-batch. Moreover, its per-iteration computation cost remains independent of the dataset size. Experimental results on image and image-text data demonstrate the effectiveness of the proposed method. Our implementation is available at https://github.com/vibalcam/GloFND .
On Discriminative Probabilistic Modeling for Self-Supervised Representation Learning
Oct 11, 2024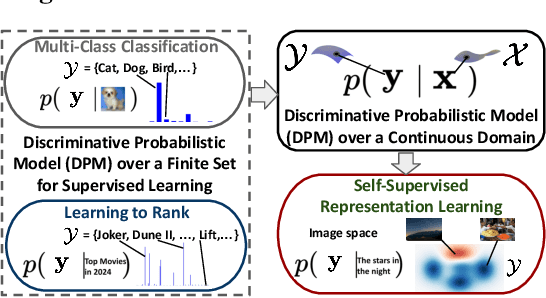
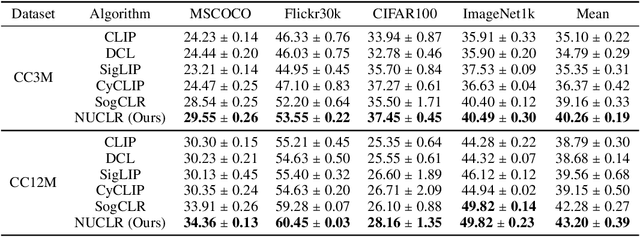
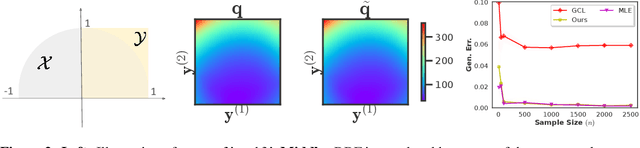

Abstract:We study the discriminative probabilistic modeling problem on a continuous domain for (multimodal) self-supervised representation learning. To address the challenge of computing the integral in the partition function for each anchor data, we leverage the multiple importance sampling (MIS) technique for robust Monte Carlo integration, which can recover InfoNCE-based contrastive loss as a special case. Within this probabilistic modeling framework, we conduct generalization error analysis to reveal the limitation of current InfoNCE-based contrastive loss for self-supervised representation learning and derive insights for developing better approaches by reducing the error of Monte Carlo integration. To this end, we propose a novel non-parametric method for approximating the sum of conditional densities required by MIS through convex optimization, yielding a new contrastive objective for self-supervised representation learning. Moreover, we design an efficient algorithm for solving the proposed objective. We empirically compare our algorithm to representative baselines on the contrastive image-language pretraining task. Experimental results on the CC3M and CC12M datasets demonstrate the superior overall performance of our algorithm.
Towards Federated Learning with On-device Training and Communication in 8-bit Floating Point
Jul 02, 2024Abstract:Recent work has shown that 8-bit floating point (FP8) can be used for efficiently training neural networks with reduced computational overhead compared to training in FP32/FP16. In this work, we investigate the use of FP8 training in a federated learning context. This brings not only the usual benefits of FP8 which are desirable for on-device training at the edge, but also reduces client-server communication costs due to significant weight compression. We present a novel method for combining FP8 client training while maintaining a global FP32 server model and provide convergence analysis. Experiments with various machine learning models and datasets show that our method consistently yields communication reductions of at least 2.9x across a variety of tasks and models compared to an FP32 baseline.
ALEXR: Optimal Single-Loop Algorithms for Convex Finite-Sum Coupled Compositional Stochastic Optimization
Dec 04, 2023



Abstract:This paper revisits a class of convex Finite-Sum Coupled Compositional Stochastic Optimization (cFCCO) problems with many applications, including group distributionally robust optimization (GDRO), reinforcement learning, and learning to rank. To better solve these problems, we introduce a unified family of efficient single-loop primal-dual block-coordinate proximal algorithms, dubbed ALEXR. This algorithm leverages block-coordinate stochastic mirror ascent updates for the dual variable and stochastic proximal gradient descent updates for the primal variable. We establish the convergence rates of ALEXR in both convex and strongly convex cases under smoothness and non-smoothness conditions of involved functions, which not only improve the best rates in previous works on smooth cFCCO problems but also expand the realm of cFCCO for solving more challenging non-smooth problems such as the dual form of GDRO. Finally, we present lower complexity bounds to demonstrate that the convergence rates of ALEXR are optimal among first-order block-coordinate stochastic algorithms for the considered class of cFCCO problems.
Everything Perturbed All at Once: Enabling Differentiable Graph Attacks
Aug 29, 2023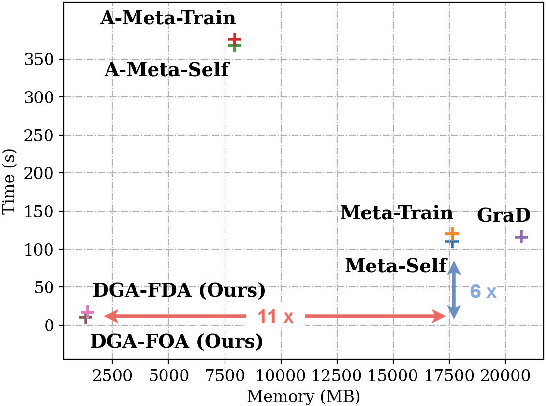

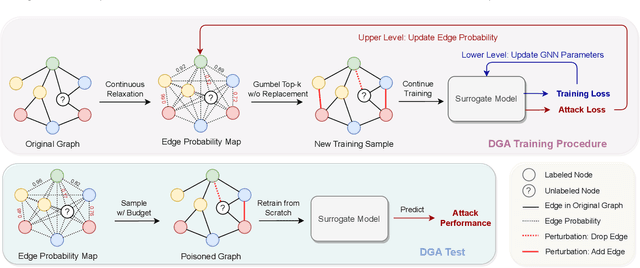

Abstract:As powerful tools for representation learning on graphs, graph neural networks (GNNs) have played an important role in applications including social networks, recommendation systems, and online web services. However, GNNs have been shown to be vulnerable to adversarial attacks, which can significantly degrade their effectiveness. Recent state-of-the-art approaches in adversarial attacks rely on gradient-based meta-learning to selectively perturb a single edge with the highest attack score until they reach the budget constraint. While effective in identifying vulnerable links, these methods are plagued by high computational costs. By leveraging continuous relaxation and parameterization of the graph structure, we propose a novel attack method called Differentiable Graph Attack (DGA) to efficiently generate effective attacks and meanwhile eliminate the need for costly retraining. Compared to the state-of-the-art, DGA achieves nearly equivalent attack performance with 6 times less training time and 11 times smaller GPU memory footprint on different benchmark datasets. Additionally, we provide extensive experimental analyses of the transferability of the DGA among different graph models, as well as its robustness against widely-used defense mechanisms.
Provable Multi-instance Deep AUC Maximization with Stochastic Pooling
May 18, 2023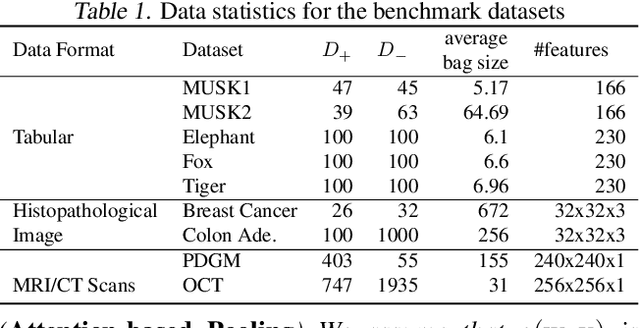
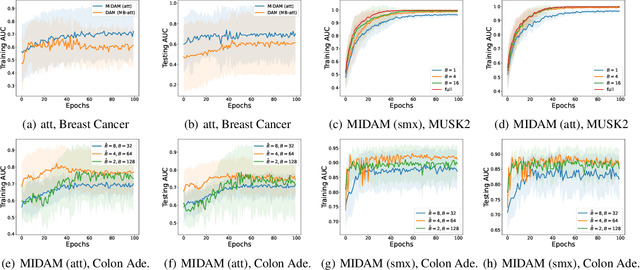

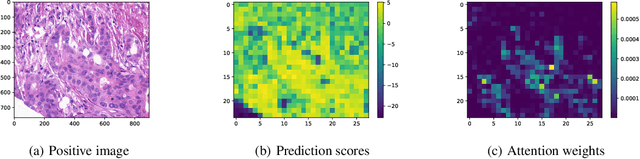
Abstract:This paper considers a novel application of deep AUC maximization (DAM) for multi-instance learning (MIL), in which a single class label is assigned to a bag of instances (e.g., multiple 2D slices of a CT scan for a patient). We address a neglected yet non-negligible computational challenge of MIL in the context of DAM, i.e., bag size is too large to be loaded into {GPU} memory for backpropagation, which is required by the standard pooling methods of MIL. To tackle this challenge, we propose variance-reduced stochastic pooling methods in the spirit of stochastic optimization by formulating the loss function over the pooled prediction as a multi-level compositional function. By synthesizing techniques from stochastic compositional optimization and non-convex min-max optimization, we propose a unified and provable muli-instance DAM (MIDAM) algorithm with stochastic smoothed-max pooling or stochastic attention-based pooling, which only samples a few instances for each bag to compute a stochastic gradient estimator and to update the model parameter. We establish a similar convergence rate of the proposed MIDAM algorithm as the state-of-the-art DAM algorithms. Our extensive experiments on conventional MIL datasets and medical datasets demonstrate the superiority of our MIDAM algorithm.
GraphFM: Improving Large-Scale GNN Training via Feature Momentum
Jun 18, 2022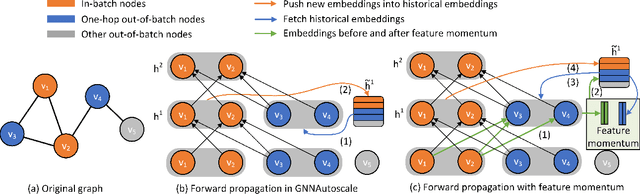

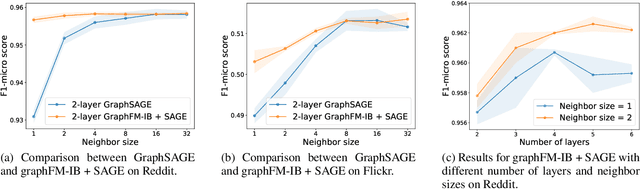

Abstract:Training of graph neural networks (GNNs) for large-scale node classification is challenging. A key difficulty lies in obtaining accurate hidden node representations while avoiding the neighborhood explosion problem. Here, we propose a new technique, named feature momentum (FM), that uses a momentum step to incorporate historical embeddings when updating feature representations. We develop two specific algorithms, known as GraphFM-IB and GraphFM-OB, that consider in-batch and out-of-batch data, respectively. GraphFM-IB applies FM to in-batch sampled data, while GraphFM-OB applies FM to out-of-batch data that are 1-hop neighborhood of in-batch data. We provide a convergence analysis for GraphFM-IB and some theoretical insight for GraphFM-OB. Empirically, we observe that GraphFM-IB can effectively alleviate the neighborhood explosion problem of existing methods. In addition, GraphFM-OB achieves promising performance on multiple large-scale graph datasets.
Optimal Algorithms for Stochastic Multi-Level Compositional Optimization
Mar 11, 2022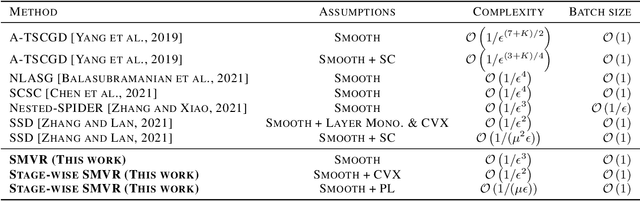
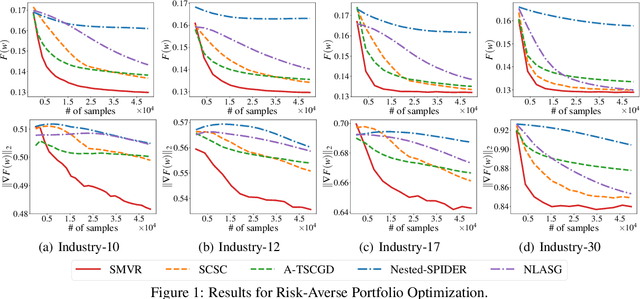
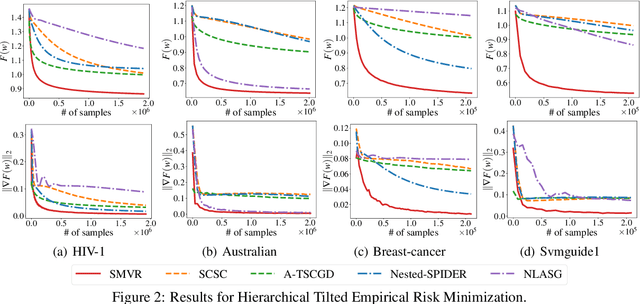

Abstract:In this paper, we investigate the problem of stochastic multi-level compositional optimization, where the objective function is a composition of multiple smooth but possibly non-convex functions. Existing methods for solving this problem either suffer from sub-optimal sample complexities or need a huge batch size. To address this limitation, we propose a Stochastic Multi-level Variance Reduction method (SMVR), which achieves the optimal sample complexity of $\mathcal{O}\left(1 / \epsilon^{3}\right)$ to find an $\epsilon$-stationary point for non-convex objectives. Furthermore, when the objective function satisfies the convexity or Polyak-{\L}ojasiewicz (PL) condition, we propose a stage-wise variant of SMVR and improve the sample complexity to $\mathcal{O}\left(1 / \epsilon^{2}\right)$ for convex functions or $\mathcal{O}\left(1 /(\mu\epsilon)\right)$ for non-convex functions satisfying the $\mu$-PL condition. The latter result implies the same complexity for $\mu$-strongly convex functions. To make use of adaptive learning rates, we also develop Adaptive SMVR, which achieves the same optimal complexities but converges faster in practice. All our complexities match the lower bounds not only in terms of $\epsilon$ but also in terms of $\mu$ (for PL or strongly convex functions), without using a large batch size in each iteration.
When AUC meets DRO: Optimizing Partial AUC for Deep Learning with Non-Convex Convergence Guarantee
Mar 04, 2022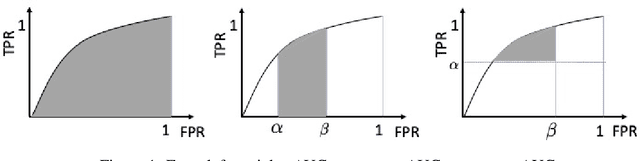
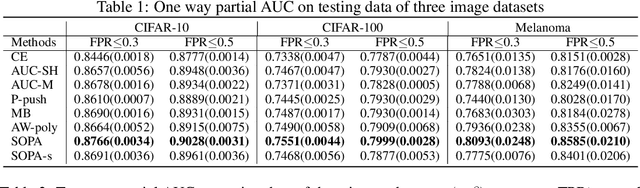
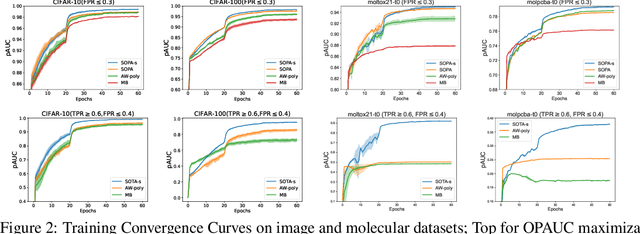
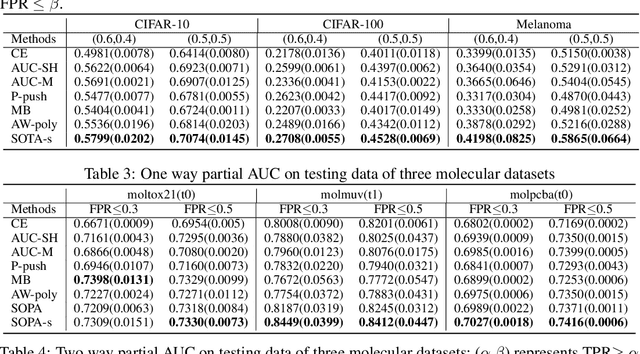
Abstract:In this paper, we propose systematic and efficient gradient-based methods for both one-way and two-way partial AUC (pAUC) maximization that are applicable to deep learning. We propose new formulations of pAUC surrogate objectives by using the distributionally robust optimization (DRO) to define the loss for each individual positive data. We consider two formulations of DRO, one of which is based on conditional-value-at-risk (CVaR) that yields a non-smooth but exact estimator for pAUC, and another one is based on a KL divergence regularized DRO that yields an inexact but smooth (soft) estimator for pAUC. For both one-way and two-way pAUC maximization, we propose two algorithms and prove their convergence for optimizing their two formulations, respectively. Experiments demonstrate the effectiveness of the proposed algorithms for pAUC maximization for deep learning on various datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge