Towards Federated Learning with On-device Training and Communication in 8-bit Floating Point

Recent work has shown that 8-bit floating point (FP8) can be used for efficiently training neural networks with reduced computational overhead compared to training in FP32/FP16. In this work, we investigate the use of FP8 training in a federated learning context. This brings not only the usual benefits of FP8 which are desirable for on-device training at the edge, but also reduces client-server communication costs due to significant weight compression. We present a novel method for combining FP8 client training while maintaining a global FP32 server model and provide convergence analysis. Experiments with various machine learning models and datasets show that our method consistently yields communication reductions of at least 2.9x across a variety of tasks and models compared to an FP32 baseline.

FedHeN: Federated Learning in Heterogeneous Networks

We propose a novel training recipe for federated learning with heterogeneous networks where each device can have different architectures. We introduce training with a side objective to the devices of higher complexities to jointly train different architectures in a federated setting. We empirically show that our approach improves the performance of different architectures and leads to high communication savings compared to the state-of-the-art methods.

Faster Convex Lipschitz Regression via 2-block ADMM

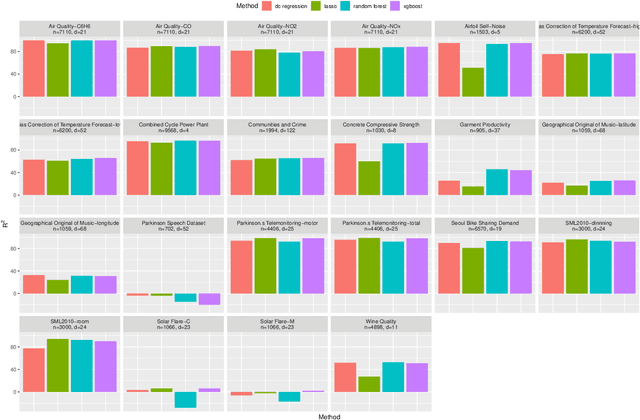
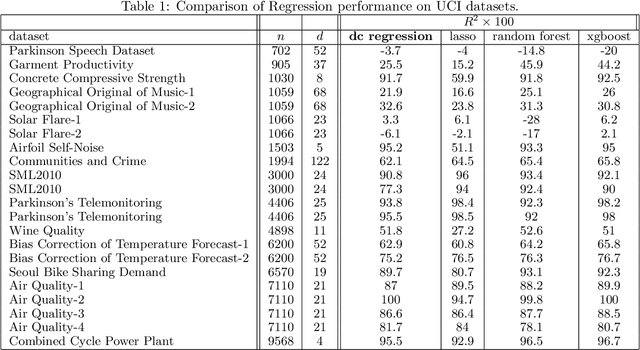
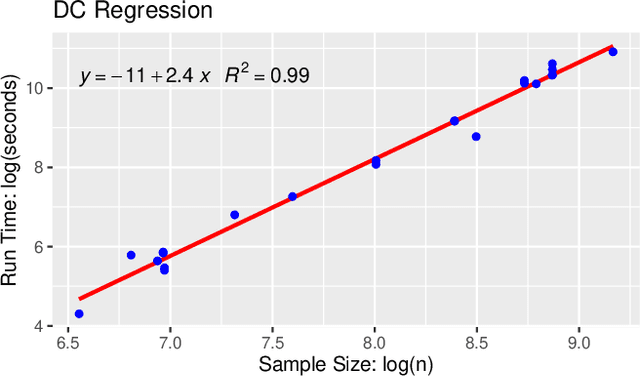
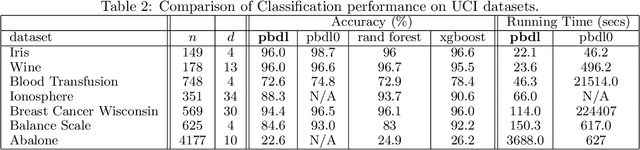
The task of approximating an arbitrary convex function arises in several learning problems such as convex regression, learning with a difference of convex (DC) functions, and approximating Bregman divergences. In this paper, we show how a broad class of convex function learning problems can be solved via a 2-block ADMM approach, where updates for each block can be computed in closed form. For the task of convex Lipschitz regression, we establish that our proposed algorithm converges with iteration complexity of $ O(n\sqrt{d}/\epsilon)$ for a dataset $ X \in \mathbb R^{n\times d}$ and $\epsilon > 0$. Combined with per-iteration computation complexity, our method converges with the rate $O(n^3 d^{1.5}/\epsilon+n^2 d^{2.5}/\epsilon+n d^3/\epsilon)$. This new rate improves the state of the art rate of $O(n^5d^2/\epsilon)$ available by interior point methods if $d = o( n^4)$. Further we provide similar solvers for DC regression and Bregman divergence learning. Unlike previous approaches, our method is amenable to the use of GPUs. We demonstrate on regression and metric learning experiments that our approach is up to 30 times faster than the existing method, and produces results that are comparable to state-of-the-art.

Federated Learning Based on Dynamic Regularization

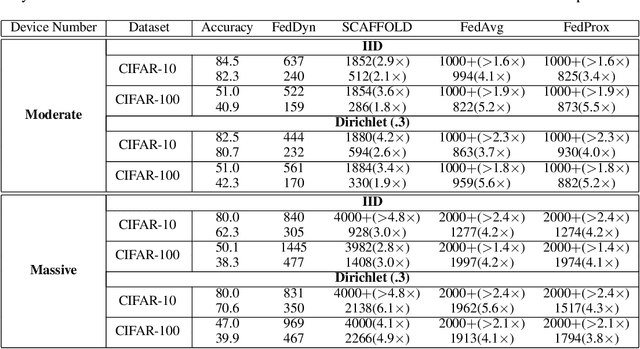
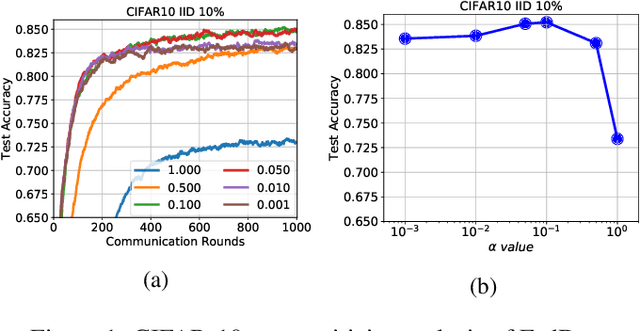
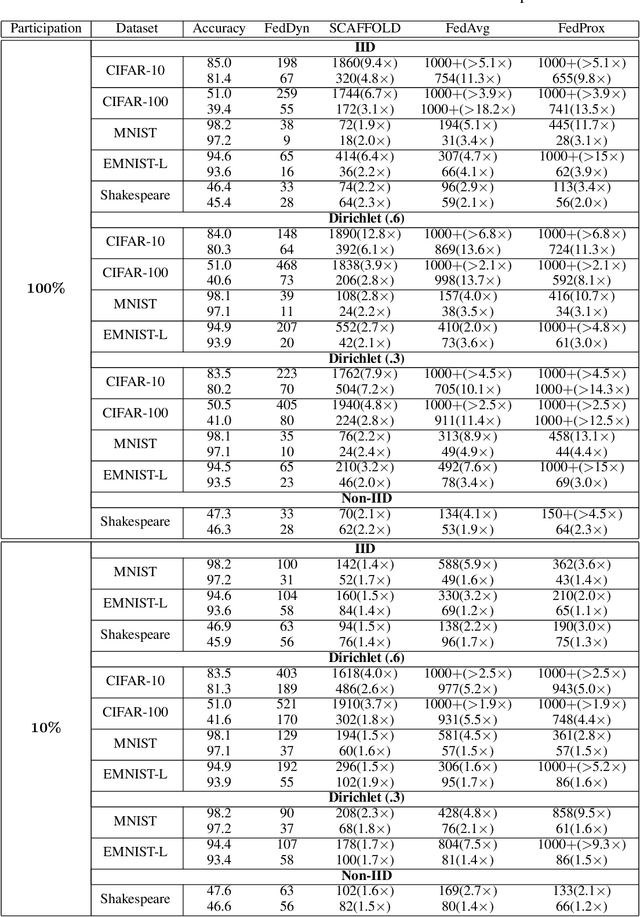
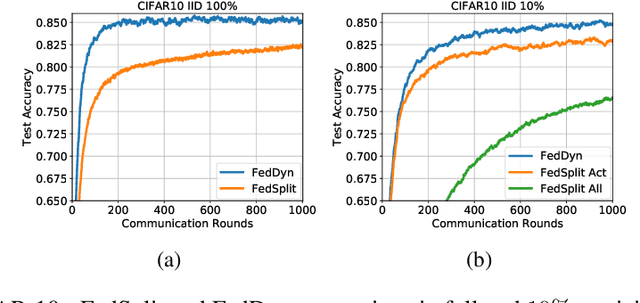
We propose a novel federated learning method for distributively training neural network models, where the server orchestrates cooperation between a subset of randomly chosen devices in each round. We view Federated Learning problem primarily from a communication perspective and allow more device level computations to save transmission costs. We point out a fundamental dilemma, in that the minima of the local-device level empirical loss are inconsistent with those of the global empirical loss. Different from recent prior works, that either attempt inexact minimization or utilize devices for parallelizing gradient computation, we propose a dynamic regularizer for each device at each round, so that in the limit the global and device solutions are aligned. We demonstrate both through empirical results on real and synthetic data as well as analytical results that our scheme leads to efficient training, in both convex and non-convex settings, while being fully agnostic to device heterogeneity and robust to large number of devices, partial participation and unbalanced data.

Budget Learning via Bracketing

Conventional machine learning applications in the mobile/IoT setting transmit data to a cloud-server for predictions. Due to cost considerations (power, latency, monetary), it is desirable to minimise device-to-server transmissions. The budget learning (BL) problem poses the learner's goal as minimising use of the cloud while suffering no discernible loss in accuracy, under the constraint that the methods employed be edge-implementable. We propose a new formulation for the BL problem via the concept of bracketings. Concretely, we propose to sandwich the cloud's prediction, $g,$ via functions $h^-, h^+$ from a `simple' class so that $h^- \le g \le h^+$ nearly always. On an instance $x$, if $h^+(x)=h^-(x)$, we leverage local processing, and bypass the cloud. We explore theoretical aspects of this formulation, providing PAC-style learnability definitions; associating the notion of budget learnability to approximability via brackets; and giving VC-theoretic analyses of their properties. We empirically validate our theory on real-world datasets, demonstrating improved performance over prior gating based methods.