Faster Convex Lipschitz Regression via 2-block ADMM
Paper and Code
Nov 29, 2021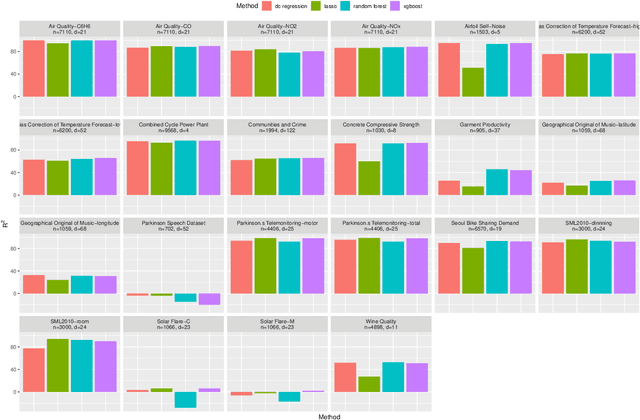
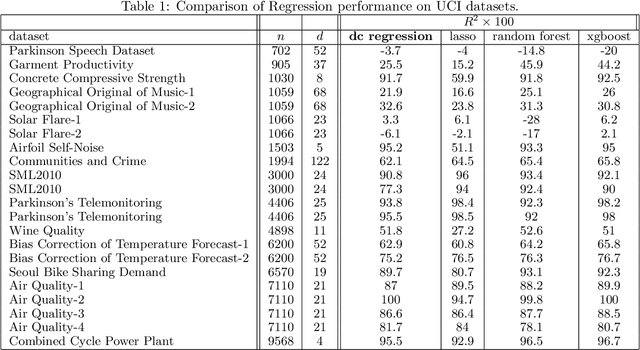
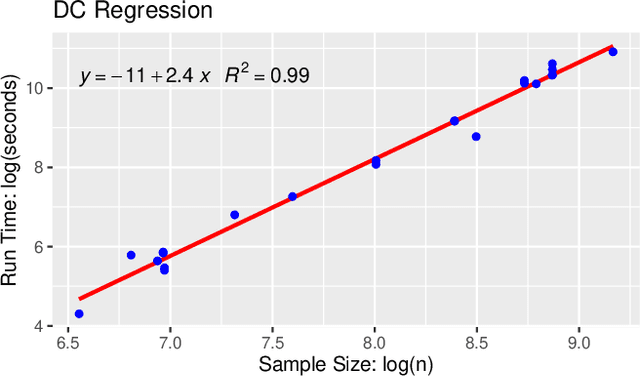
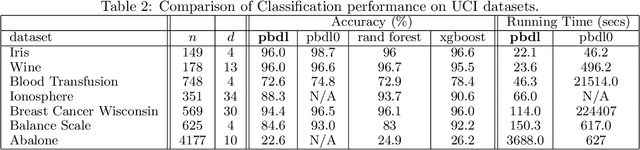
The task of approximating an arbitrary convex function arises in several learning problems such as convex regression, learning with a difference of convex (DC) functions, and approximating Bregman divergences. In this paper, we show how a broad class of convex function learning problems can be solved via a 2-block ADMM approach, where updates for each block can be computed in closed form. For the task of convex Lipschitz regression, we establish that our proposed algorithm converges with iteration complexity of $ O(n\sqrt{d}/\epsilon)$ for a dataset $ X \in \mathbb R^{n\times d}$ and $\epsilon > 0$. Combined with per-iteration computation complexity, our method converges with the rate $O(n^3 d^{1.5}/\epsilon+n^2 d^{2.5}/\epsilon+n d^3/\epsilon)$. This new rate improves the state of the art rate of $O(n^5d^2/\epsilon)$ available by interior point methods if $d = o( n^4)$. Further we provide similar solvers for DC regression and Bregman divergence learning. Unlike previous approaches, our method is amenable to the use of GPUs. We demonstrate on regression and metric learning experiments that our approach is up to 30 times faster than the existing method, and produces results that are comparable to state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge