Faster Convex Lipschitz Regression via 2-block ADMM

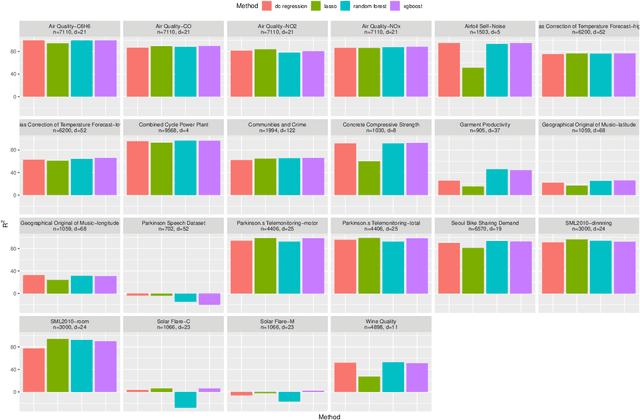
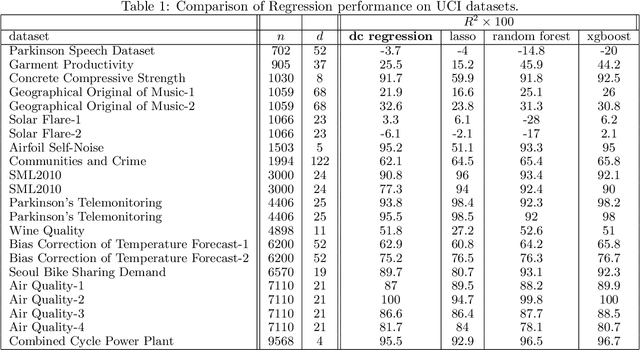
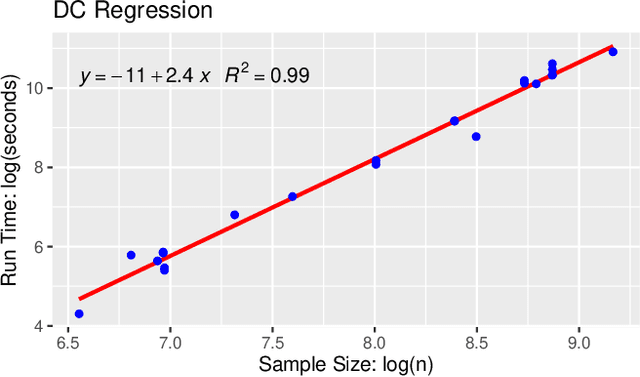
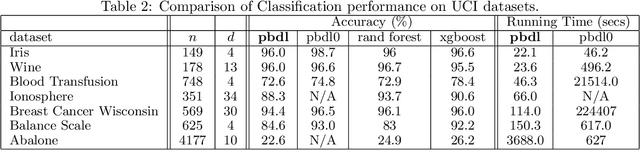
The task of approximating an arbitrary convex function arises in several learning problems such as convex regression, learning with a difference of convex (DC) functions, and approximating Bregman divergences. In this paper, we show how a broad class of convex function learning problems can be solved via a 2-block ADMM approach, where updates for each block can be computed in closed form. For the task of convex Lipschitz regression, we establish that our proposed algorithm converges with iteration complexity of $ O(n\sqrt{d}/\epsilon)$ for a dataset $ X \in \mathbb R^{n\times d}$ and $\epsilon > 0$. Combined with per-iteration computation complexity, our method converges with the rate $O(n^3 d^{1.5}/\epsilon+n^2 d^{2.5}/\epsilon+n d^3/\epsilon)$. This new rate improves the state of the art rate of $O(n^5d^2/\epsilon)$ available by interior point methods if $d = o( n^4)$. Further we provide similar solvers for DC regression and Bregman divergence learning. Unlike previous approaches, our method is amenable to the use of GPUs. We demonstrate on regression and metric learning experiments that our approach is up to 30 times faster than the existing method, and produces results that are comparable to state-of-the-art.

Interpretable Visualization and Higher-Order Dimension Reduction for ECoG Data

ElectroCOrticoGraphy (ECoG) technology measures electrical activity in the human brain via electrodes placed directly on the cortical surface during neurosurgery. Through its capability to record activity at a fast temporal resolution, ECoG experiments have allowed scientists to better understand how the human brain processes speech. By its nature, ECoG data is difficult for neuroscientists to directly interpret for two major reasons. Firstly, ECoG data tends to be large in size, as each individual experiment yields data up to several gigabytes. Secondly, ECoG data has a complex, higher-order nature. After signal processing, this type of data may be organized as a 4-way tensor with dimensions representing trials, electrodes, frequency, and time. In this paper, we develop an interpretable dimension reduction approach called Regularized Higher Order Principal Components Analysis, as well as an extension to Regularized Higher Order Partial Least Squares, that allows neuroscientists to explore and visualize ECoG data. Our approach employs a sparse and functional Candecomp-Parafac (CP) decomposition that incorporates sparsity to select relevant electrodes and frequency bands, as well as smoothness over time and frequency, yielding directly interpretable factors. We demonstrate the performance and interpretability of our method with an ECoG case study on audio and visual processing of human speech.