Unsupervised Machine Learning for Scientific Discovery: Workflow and Best Practices

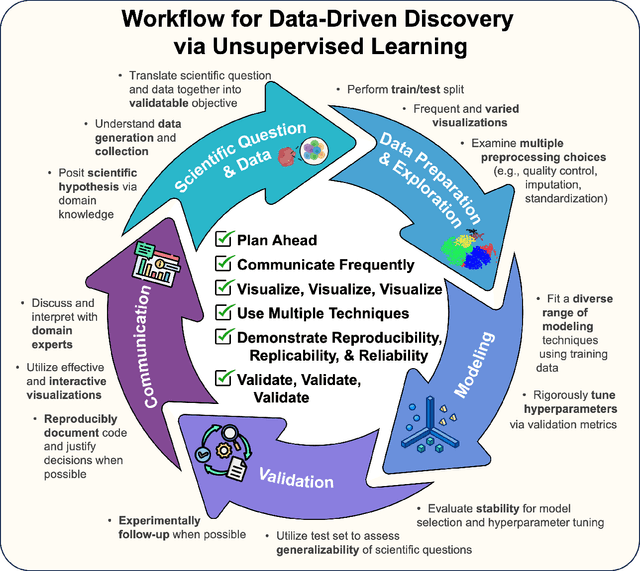
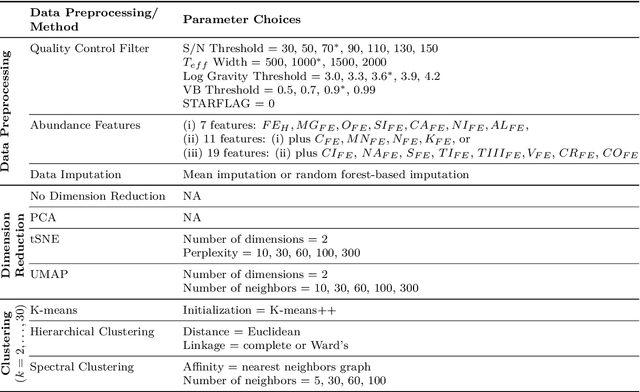
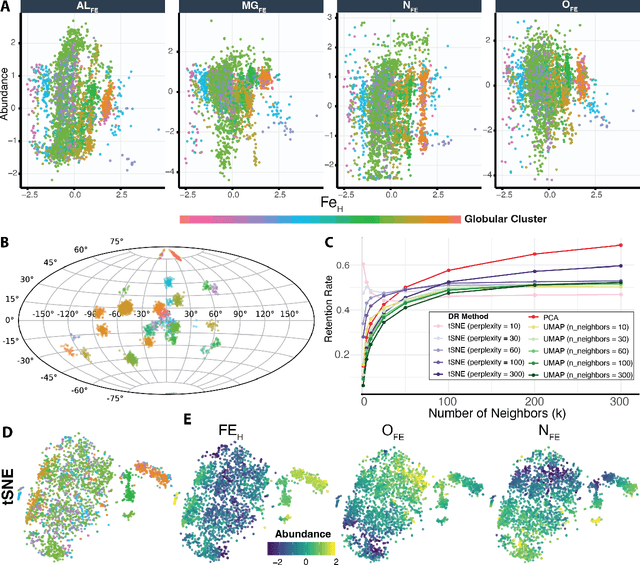
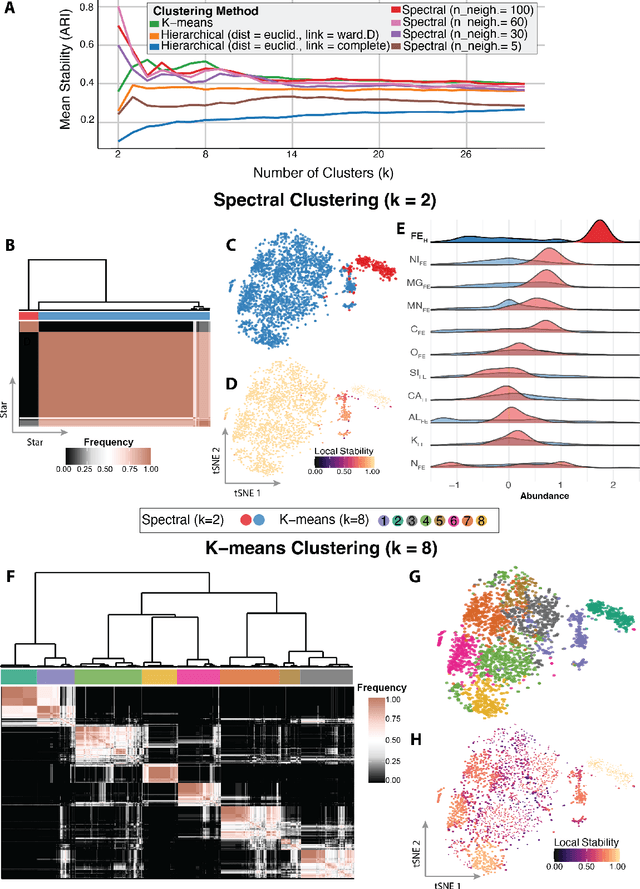
Unsupervised machine learning is widely used to mine large, unlabeled datasets to make data-driven discoveries in critical domains such as climate science, biomedicine, astronomy, chemistry, and more. However, despite its widespread utilization, there is a lack of standardization in unsupervised learning workflows for making reliable and reproducible scientific discoveries. In this paper, we present a structured workflow for using unsupervised learning techniques in science. We highlight and discuss best practices starting with formulating validatable scientific questions, conducting robust data preparation and exploration, using a range of modeling techniques, performing rigorous validation by evaluating the stability and generalizability of unsupervised learning conclusions, and promoting effective communication and documentation of results to ensure reproducible scientific discoveries. To illustrate our proposed workflow, we present a case study from astronomy, seeking to refine globular clusters of Milky Way stars based upon their chemical composition. Our case study highlights the importance of validation and illustrates how the benefits of a carefully-designed workflow for unsupervised learning can advance scientific discovery.

Are machine learning interpretations reliable? A stability study on global interpretations

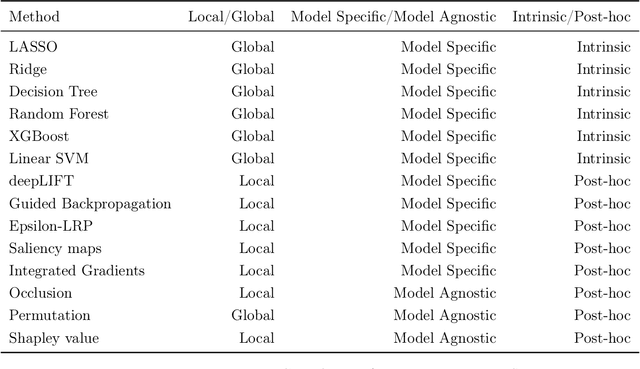
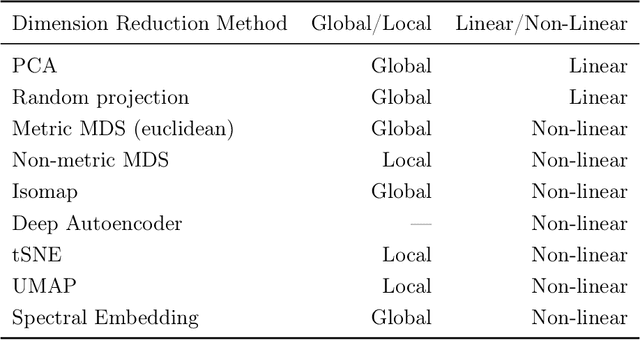
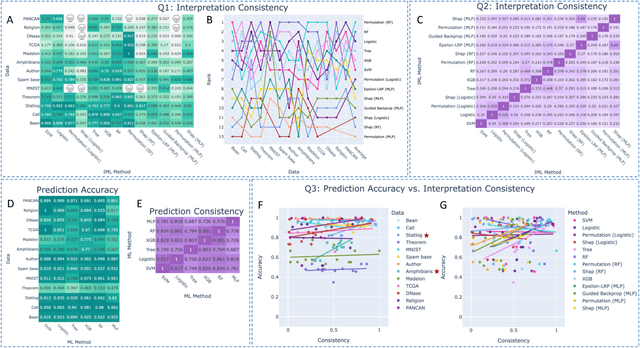
As machine learning systems are increasingly used in high-stakes domains, there is a growing emphasis placed on making them interpretable to improve trust in these systems. In response, a range of interpretable machine learning (IML) methods have been developed to generate human-understandable insights into otherwise black box models. With these methods, a fundamental question arises: Are these interpretations reliable? Unlike with prediction accuracy or other evaluation metrics for supervised models, the proximity to the true interpretation is difficult to define. Instead, we ask a closely related question that we argue is a prerequisite for reliability: Are these interpretations stable? We define stability as findings that are consistent or reliable under small random perturbations to the data or algorithms. In this study, we conduct the first systematic, large-scale empirical stability study on popular machine learning global interpretations for both supervised and unsupervised tasks on tabular data. Our findings reveal that popular interpretation methods are frequently unstable, notably less stable than the predictions themselves, and that there is no association between the accuracy of machine learning predictions and the stability of their associated interpretations. Moreover, we show that no single method consistently provides the most stable interpretations across a range of benchmark datasets. Overall, these results suggest that interpretability alone does not warrant trust, and underscores the need for rigorous evaluation of interpretation stability in future work. To support these principles, we have developed and released an open source IML dashboard and Python package to enable researchers to assess the stability and reliability of their own data-driven interpretations and discoveries.

Cluster Quilting: Spectral Clustering for Patchwork Learning

Patchwork learning arises as a new and challenging data collection paradigm where both samples and features are observed in fragmented subsets. Due to technological limits, measurement expense, or multimodal data integration, such patchwork data structures are frequently seen in neuroscience, healthcare, and genomics, among others. Instead of analyzing each data patch separately, it is highly desirable to extract comprehensive knowledge from the whole data set. In this work, we focus on the clustering problem in patchwork learning, aiming at discovering clusters amongst all samples even when some are never jointly observed for any feature. We propose a novel spectral clustering method called Cluster Quilting, consisting of (i) patch ordering that exploits the overlapping structure amongst all patches, (ii) patchwise SVD, (iii) sequential linear mapping of top singular vectors for patch overlaps, followed by (iv) k-means on the combined and weighted singular vectors. Under a sub-Gaussian mixture model, we establish theoretical guarantees via a non-asymptotic misclustering rate bound that reflects both properties of the patch-wise observation regime as well as the clustering signal and noise dependencies. We also validate our Cluster Quilting algorithm through extensive empirical studies on both simulated and real data sets in neuroscience and genomics, where it discovers more accurate and scientifically more plausible clusters than other approaches.

Fair MP-BOOST: Fair and Interpretable Minipatch Boosting

Ensemble methods, particularly boosting, have established themselves as highly effective and widely embraced machine learning techniques for tabular data. In this paper, we aim to leverage the robust predictive power of traditional boosting methods while enhancing fairness and interpretability. To achieve this, we develop Fair MP-Boost, a stochastic boosting scheme that balances fairness and accuracy by adaptively learning features and observations during training. Specifically, Fair MP-Boost sequentially samples small subsets of observations and features, termed minipatches (MP), according to adaptively learned feature and observation sampling probabilities. We devise these probabilities by combining loss functions, or by combining feature importance scores to address accuracy and fairness simultaneously. Hence, Fair MP-Boost prioritizes important and fair features along with challenging instances, to select the most relevant minipatches for learning. The learned probability distributions also yield intrinsic interpretations of feature importance and important observations in Fair MP-Boost. Through empirical evaluation of simulated and benchmark datasets, we showcase the interpretability, accuracy, and fairness of Fair MP-Boost.

Fair Feature Importance Scores for Interpreting Tree-Based Methods and Surrogates

Across various sectors such as healthcare, criminal justice, national security, finance, and technology, large-scale machine learning (ML) and artificial intelligence (AI) systems are being deployed to make critical data-driven decisions. Many have asked if we can and should trust these ML systems to be making these decisions. Two critical components are prerequisites for trust in ML systems: interpretability, or the ability to understand why the ML system makes the decisions it does, and fairness, which ensures that ML systems do not exhibit bias against certain individuals or groups. Both interpretability and fairness are important and have separately received abundant attention in the ML literature, but so far, there have been very few methods developed to directly interpret models with regard to their fairness. In this paper, we focus on arguably the most popular type of ML interpretation: feature importance scores. Inspired by the use of decision trees in knowledge distillation, we propose to leverage trees as interpretable surrogates for complex black-box ML models. Specifically, we develop a novel fair feature importance score for trees that can be used to interpret how each feature contributes to fairness or bias in trees, tree-based ensembles, or tree-based surrogates of any complex ML system. Like the popular mean decrease in impurity for trees, our Fair Feature Importance Score is defined based on the mean decrease (or increase) in group bias. Through simulations as well as real examples on benchmark fairness datasets, we demonstrate that our Fair Feature Importance Score offers valid interpretations for both tree-based ensembles and tree-based surrogates of other ML systems.

Data Augmentation via Subgroup Mixup for Improving Fairness

In this work, we propose data augmentation via pairwise mixup across subgroups to improve group fairness. Many real-world applications of machine learning systems exhibit biases across certain groups due to under-representation or training data that reflects societal biases. Inspired by the successes of mixup for improving classification performance, we develop a pairwise mixup scheme to augment training data and encourage fair and accurate decision boundaries for all subgroups. Data augmentation for group fairness allows us to add new samples of underrepresented groups to balance subpopulations. Furthermore, our method allows us to use the generalization ability of mixup to improve both fairness and accuracy. We compare our proposed mixup to existing data augmentation and bias mitigation approaches on both synthetic simulations and real-world benchmark fair classification data, demonstrating that we are able to achieve fair outcomes with robust if not improved accuracy.

Interpretable Machine Learning for Discovery: Statistical Challenges \& Opportunities

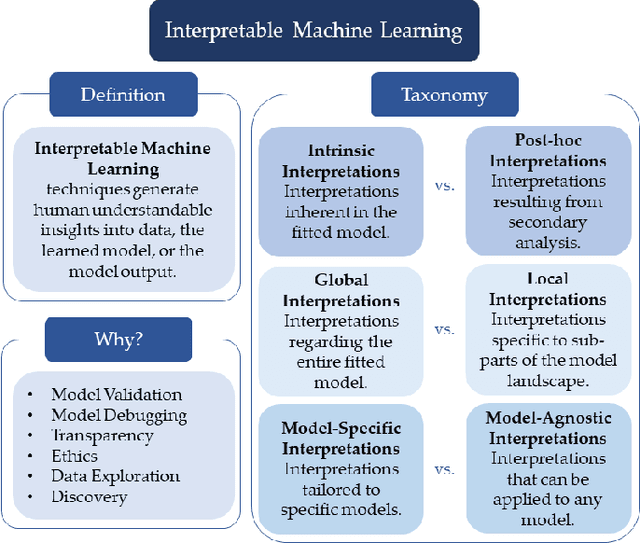
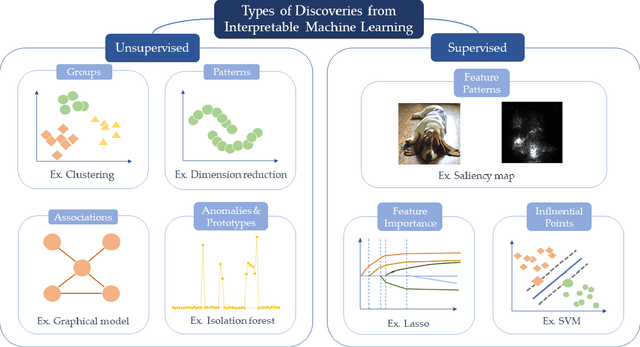
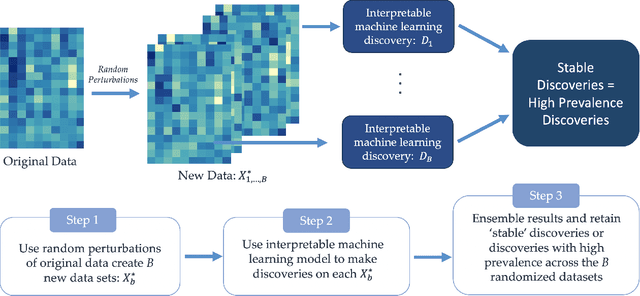
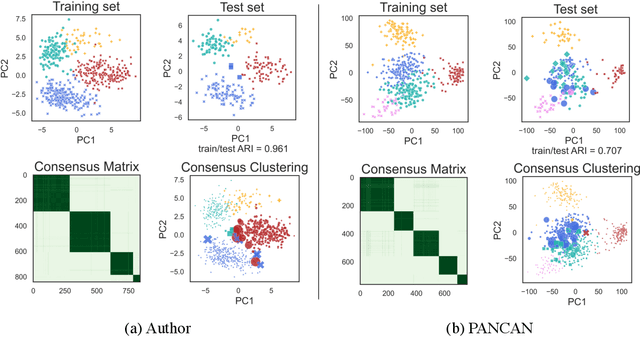
New technologies have led to vast troves of large and complex datasets across many scientific domains and industries. People routinely use machine learning techniques to not only process, visualize, and make predictions from this big data, but also to make data-driven discoveries. These discoveries are often made using Interpretable Machine Learning, or machine learning models and techniques that yield human understandable insights. In this paper, we discuss and review the field of interpretable machine learning, focusing especially on the techniques as they are often employed to generate new knowledge or make discoveries from large data sets. We outline the types of discoveries that can be made using Interpretable Machine Learning in both supervised and unsupervised settings. Additionally, we focus on the grand challenge of how to validate these discoveries in a data-driven manner, which promotes trust in machine learning systems and reproducibility in science. We discuss validation from both a practical perspective, reviewing approaches based on data-splitting and stability, as well as from a theoretical perspective, reviewing statistical results on model selection consistency and uncertainty quantification via statistical inference. Finally, we conclude by highlighting open challenges in using interpretable machine learning techniques to make discoveries, including gaps between theory and practice for validating data-driven-discoveries.

Nonparanormal Graph Quilting with Applications to Calcium Imaging

Probabilistic graphical models have become an important unsupervised learning tool for detecting network structures for a variety of problems, including the estimation of functional neuronal connectivity from two-photon calcium imaging data. However, in the context of calcium imaging, technological limitations only allow for partially overlapping layers of neurons in a brain region of interest to be jointly recorded. In this case, graph estimation for the full data requires inference for edge selection when many pairs of neurons have no simultaneous observations. This leads to the Graph Quilting problem, which seeks to estimate a graph in the presence of block-missingness in the empirical covariance matrix. Solutions for the Graph Quilting problem have previously been studied for Gaussian graphical models; however, neural activity data from calcium imaging are often non-Gaussian, thereby requiring a more flexible modeling approach. Thus, in our work, we study two approaches for nonparanormal Graph Quilting based on the Gaussian copula graphical model, namely a maximum likelihood procedure and a low-rank based framework. We provide theoretical guarantees on edge recovery for the former approach under similar conditions to those previously developed for the Gaussian setting, and we investigate the empirical performance of both methods using simulations as well as real data calcium imaging data. Our approaches yield more scientifically meaningful functional connectivity estimates compared to existing Gaussian graph quilting methods for this calcium imaging data set.

Low-Rank Covariance Completion for Graph Quilting with Applications to Functional Connectivity

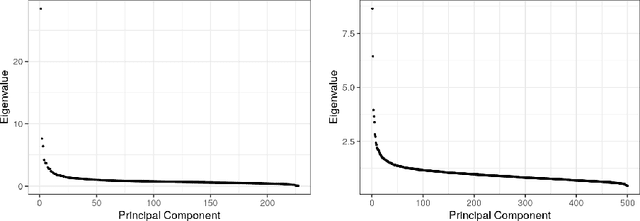
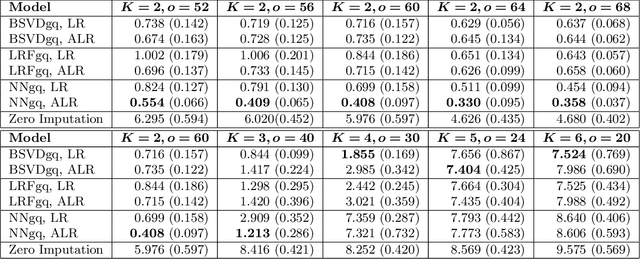
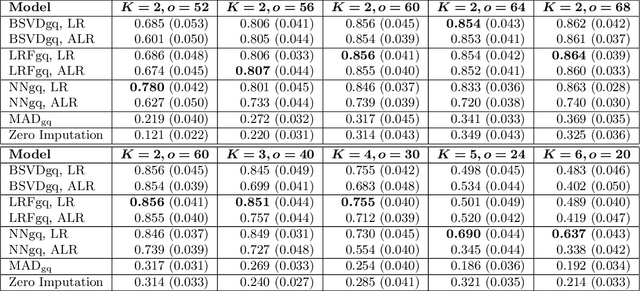
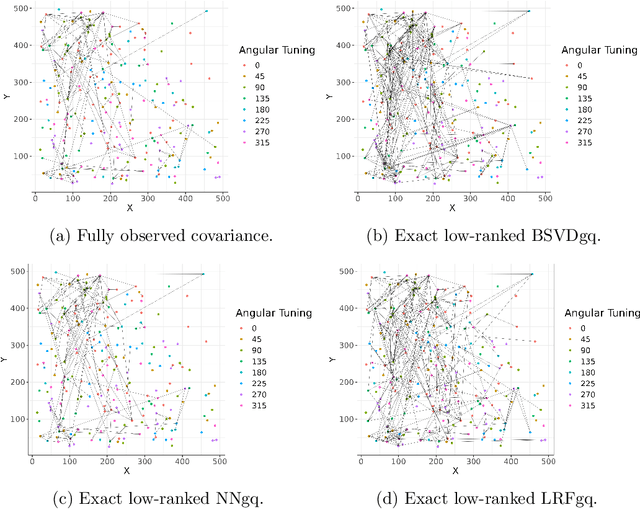
As a tool for estimating networks in high dimensions, graphical models are commonly applied to calcium imaging data to estimate functional neuronal connectivity, i.e. relationships between the activities of neurons. However, in many calcium imaging data sets, the full population of neurons is not recorded simultaneously, but instead in partially overlapping blocks. This leads to the Graph Quilting problem, as first introduced by (Vinci et.al. 2019), in which the goal is to infer the structure of the full graph when only subsets of features are jointly observed. In this paper, we study a novel two-step approach to Graph Quilting, which first imputes the complete covariance matrix using low-rank covariance completion techniques before estimating the graph structure. We introduce three approaches to solve this problem: block singular value decomposition, nuclear norm penalization, and non-convex low-rank factorization. While prior works have studied low-rank matrix completion, we address the challenges brought by the block-wise missingness and are the first to investigate the problem in the context of graph learning. We discuss theoretical properties of the two-step procedure, showing graph selection consistency of one proposed approach by proving novel L infinity-norm error bounds for matrix completion with block-missingness. We then investigate the empirical performance of the proposed methods on simulations and on real-world data examples, through which we show the efficacy of these methods for estimating functional connectivity from calcium imaging data.

Inference for Interpretable Machine Learning: Fast, Model-Agnostic Confidence Intervals for Feature Importance

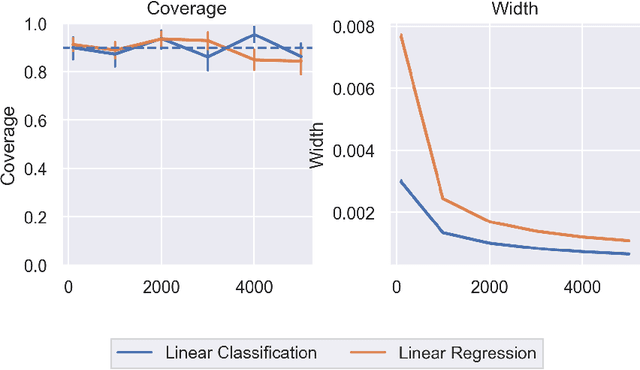
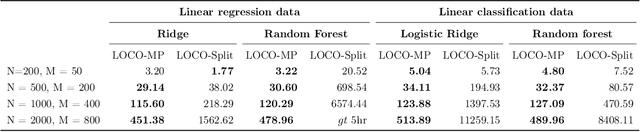
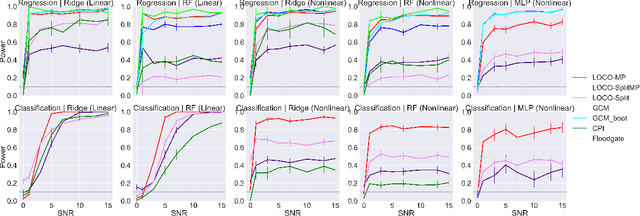
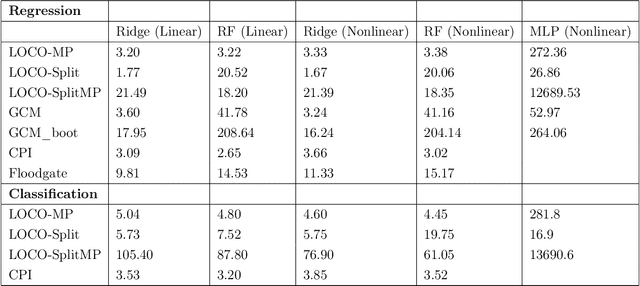
In order to trust machine learning for high-stakes problems, we need models to be both reliable and interpretable. Recently, there has been a growing body of work on interpretable machine learning which generates human understandable insights into data, models, or predictions. At the same time, there has been increased interest in quantifying the reliability and uncertainty of machine learning predictions, often in the form of confidence intervals for predictions using conformal inference. Yet, there has been relatively little attention given to the reliability and uncertainty of machine learning interpretations, which is the focus of this paper. Our goal is to develop confidence intervals for a widely-used form of machine learning interpretation: feature importance. We specifically seek to develop universal model-agnostic and assumption-light confidence intervals for feature importance that will be valid for any machine learning model and for any regression or classification task. We do so by leveraging a form of random observation and feature subsampling called minipatch ensembles and show that our approach provides assumption-light asymptotic coverage for the feature importance score of any model. Further, our approach is fast as computations needed for inference come nearly for free as part of the ensemble learning process. Finally, we also show that our same procedure can be leveraged to provide valid confidence intervals for predictions, hence providing fast, simultaneous quantification of the uncertainty of both model predictions and interpretations. We validate our intervals on a series of synthetic and real data examples, showing that our approach detects the correct important features and exhibits many computational and statistical advantages over existing methods.