Cluster Quilting: Spectral Clustering for Patchwork Learning

Patchwork learning arises as a new and challenging data collection paradigm where both samples and features are observed in fragmented subsets. Due to technological limits, measurement expense, or multimodal data integration, such patchwork data structures are frequently seen in neuroscience, healthcare, and genomics, among others. Instead of analyzing each data patch separately, it is highly desirable to extract comprehensive knowledge from the whole data set. In this work, we focus on the clustering problem in patchwork learning, aiming at discovering clusters amongst all samples even when some are never jointly observed for any feature. We propose a novel spectral clustering method called Cluster Quilting, consisting of (i) patch ordering that exploits the overlapping structure amongst all patches, (ii) patchwise SVD, (iii) sequential linear mapping of top singular vectors for patch overlaps, followed by (iv) k-means on the combined and weighted singular vectors. Under a sub-Gaussian mixture model, we establish theoretical guarantees via a non-asymptotic misclustering rate bound that reflects both properties of the patch-wise observation regime as well as the clustering signal and noise dependencies. We also validate our Cluster Quilting algorithm through extensive empirical studies on both simulated and real data sets in neuroscience and genomics, where it discovers more accurate and scientifically more plausible clusters than other approaches.

Nonparanormal Graph Quilting with Applications to Calcium Imaging

Probabilistic graphical models have become an important unsupervised learning tool for detecting network structures for a variety of problems, including the estimation of functional neuronal connectivity from two-photon calcium imaging data. However, in the context of calcium imaging, technological limitations only allow for partially overlapping layers of neurons in a brain region of interest to be jointly recorded. In this case, graph estimation for the full data requires inference for edge selection when many pairs of neurons have no simultaneous observations. This leads to the Graph Quilting problem, which seeks to estimate a graph in the presence of block-missingness in the empirical covariance matrix. Solutions for the Graph Quilting problem have previously been studied for Gaussian graphical models; however, neural activity data from calcium imaging are often non-Gaussian, thereby requiring a more flexible modeling approach. Thus, in our work, we study two approaches for nonparanormal Graph Quilting based on the Gaussian copula graphical model, namely a maximum likelihood procedure and a low-rank based framework. We provide theoretical guarantees on edge recovery for the former approach under similar conditions to those previously developed for the Gaussian setting, and we investigate the empirical performance of both methods using simulations as well as real data calcium imaging data. Our approaches yield more scientifically meaningful functional connectivity estimates compared to existing Gaussian graph quilting methods for this calcium imaging data set.

Low-Rank Covariance Completion for Graph Quilting with Applications to Functional Connectivity

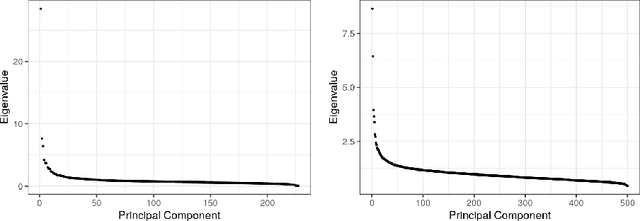
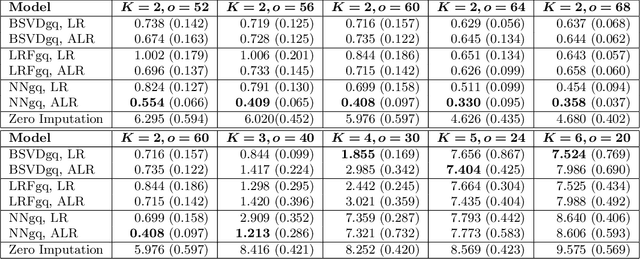
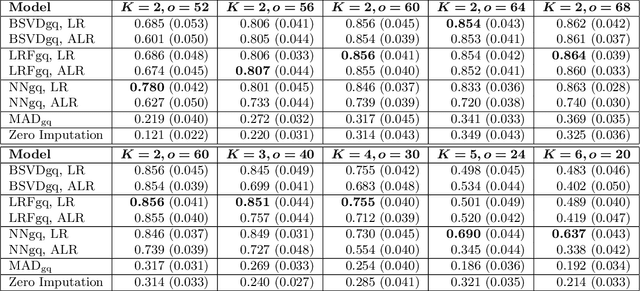
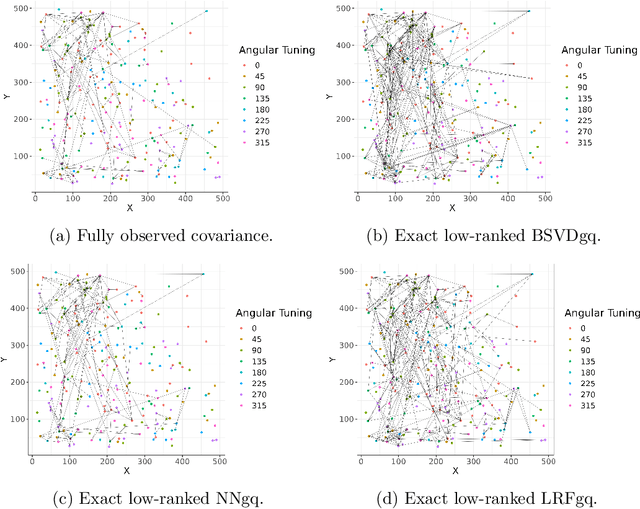
As a tool for estimating networks in high dimensions, graphical models are commonly applied to calcium imaging data to estimate functional neuronal connectivity, i.e. relationships between the activities of neurons. However, in many calcium imaging data sets, the full population of neurons is not recorded simultaneously, but instead in partially overlapping blocks. This leads to the Graph Quilting problem, as first introduced by (Vinci et.al. 2019), in which the goal is to infer the structure of the full graph when only subsets of features are jointly observed. In this paper, we study a novel two-step approach to Graph Quilting, which first imputes the complete covariance matrix using low-rank covariance completion techniques before estimating the graph structure. We introduce three approaches to solve this problem: block singular value decomposition, nuclear norm penalization, and non-convex low-rank factorization. While prior works have studied low-rank matrix completion, we address the challenges brought by the block-wise missingness and are the first to investigate the problem in the context of graph learning. We discuss theoretical properties of the two-step procedure, showing graph selection consistency of one proposed approach by proving novel L infinity-norm error bounds for matrix completion with block-missingness. We then investigate the empirical performance of the proposed methods on simulations and on real-world data examples, through which we show the efficacy of these methods for estimating functional connectivity from calcium imaging data.

Interpretable Visualization and Higher-Order Dimension Reduction for ECoG Data

ElectroCOrticoGraphy (ECoG) technology measures electrical activity in the human brain via electrodes placed directly on the cortical surface during neurosurgery. Through its capability to record activity at a fast temporal resolution, ECoG experiments have allowed scientists to better understand how the human brain processes speech. By its nature, ECoG data is difficult for neuroscientists to directly interpret for two major reasons. Firstly, ECoG data tends to be large in size, as each individual experiment yields data up to several gigabytes. Secondly, ECoG data has a complex, higher-order nature. After signal processing, this type of data may be organized as a 4-way tensor with dimensions representing trials, electrodes, frequency, and time. In this paper, we develop an interpretable dimension reduction approach called Regularized Higher Order Principal Components Analysis, as well as an extension to Regularized Higher Order Partial Least Squares, that allows neuroscientists to explore and visualize ECoG data. Our approach employs a sparse and functional Candecomp-Parafac (CP) decomposition that incorporates sparsity to select relevant electrodes and frequency bands, as well as smoothness over time and frequency, yielding directly interpretable factors. We demonstrate the performance and interpretability of our method with an ECoG case study on audio and visual processing of human speech.