Unsupervised Machine Learning for Scientific Discovery: Workflow and Best Practices

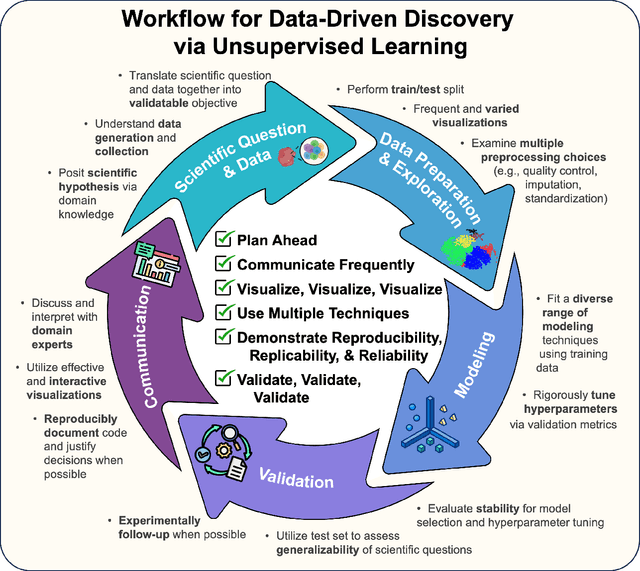
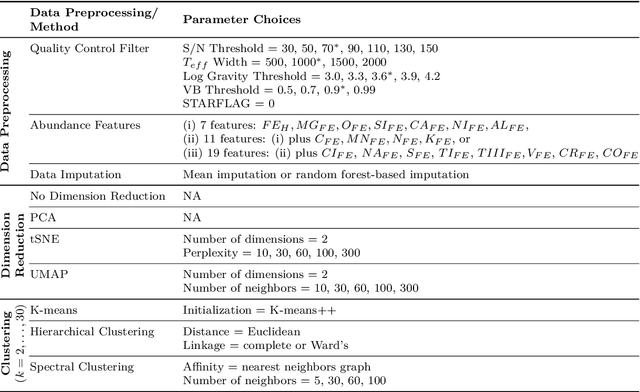
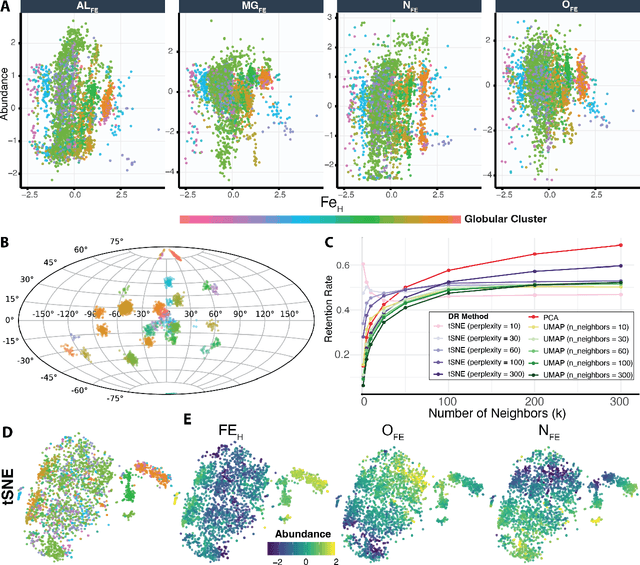
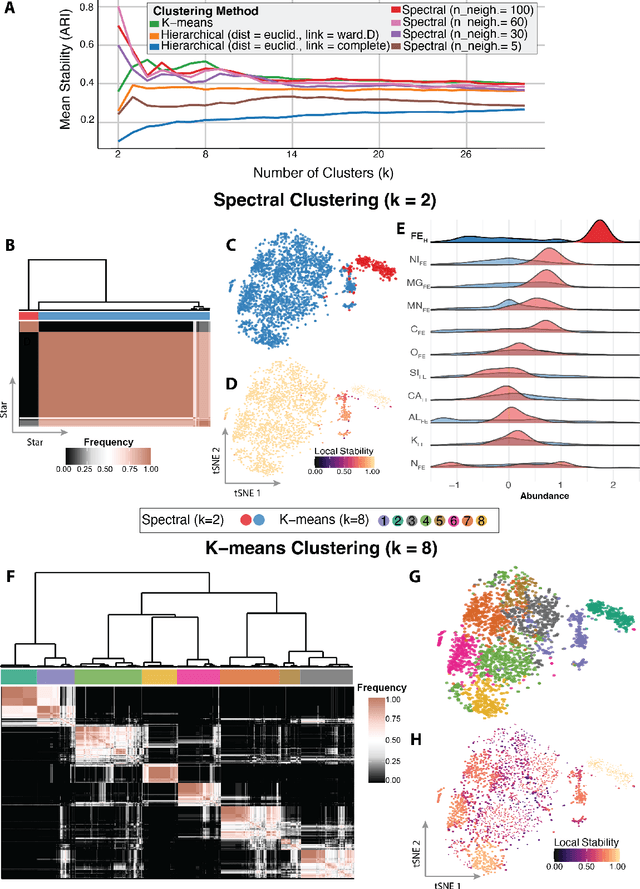
Unsupervised machine learning is widely used to mine large, unlabeled datasets to make data-driven discoveries in critical domains such as climate science, biomedicine, astronomy, chemistry, and more. However, despite its widespread utilization, there is a lack of standardization in unsupervised learning workflows for making reliable and reproducible scientific discoveries. In this paper, we present a structured workflow for using unsupervised learning techniques in science. We highlight and discuss best practices starting with formulating validatable scientific questions, conducting robust data preparation and exploration, using a range of modeling techniques, performing rigorous validation by evaluating the stability and generalizability of unsupervised learning conclusions, and promoting effective communication and documentation of results to ensure reproducible scientific discoveries. To illustrate our proposed workflow, we present a case study from astronomy, seeking to refine globular clusters of Milky Way stars based upon their chemical composition. Our case study highlights the importance of validation and illustrates how the benefits of a carefully-designed workflow for unsupervised learning can advance scientific discovery.

MDI+: A Flexible Random Forest-Based Feature Importance Framework

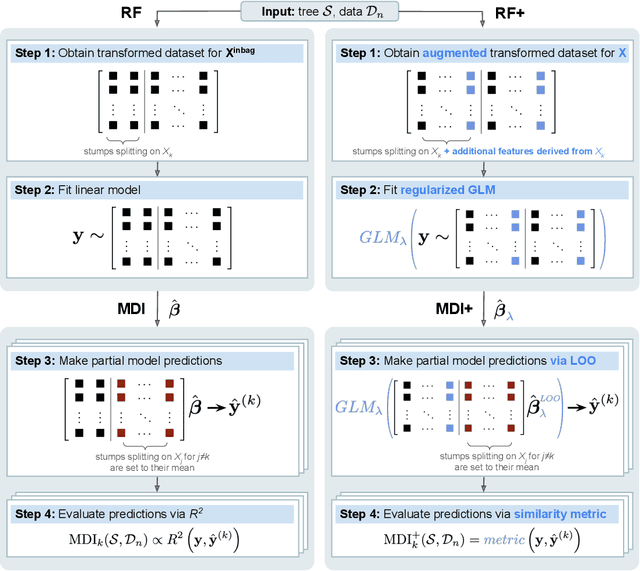
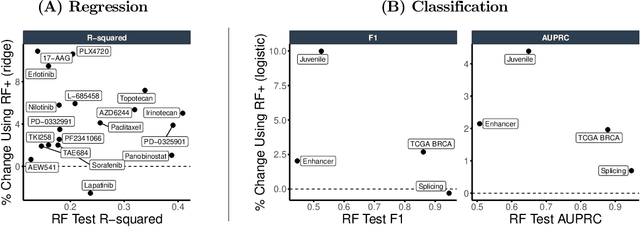
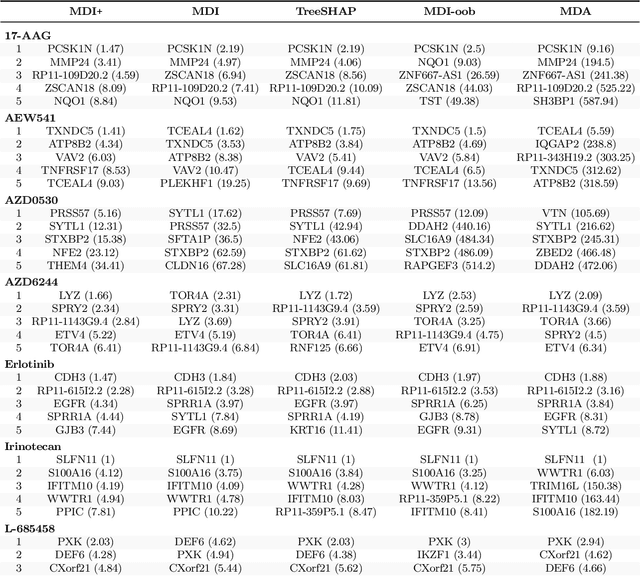
Mean decrease in impurity (MDI) is a popular feature importance measure for random forests (RFs). We show that the MDI for a feature $X_k$ in each tree in an RF is equivalent to the unnormalized $R^2$ value in a linear regression of the response on the collection of decision stumps that split on $X_k$. We use this interpretation to propose a flexible feature importance framework called MDI+. Specifically, MDI+ generalizes MDI by allowing the analyst to replace the linear regression model and $R^2$ metric with regularized generalized linear models (GLMs) and metrics better suited for the given data structure. Moreover, MDI+ incorporates additional features to mitigate known biases of decision trees against additive or smooth models. We further provide guidance on how practitioners can choose an appropriate GLM and metric based upon the Predictability, Computability, Stability framework for veridical data science. Extensive data-inspired simulations show that MDI+ significantly outperforms popular feature importance measures in identifying signal features. We also apply MDI+ to two real-world case studies on drug response prediction and breast cancer subtype classification. We show that MDI+ extracts well-established predictive genes with significantly greater stability compared to existing feature importance measures. All code and models are released in a full-fledged python package on Github.

Feature Selection for Data Integration with Mixed Multi-view Data

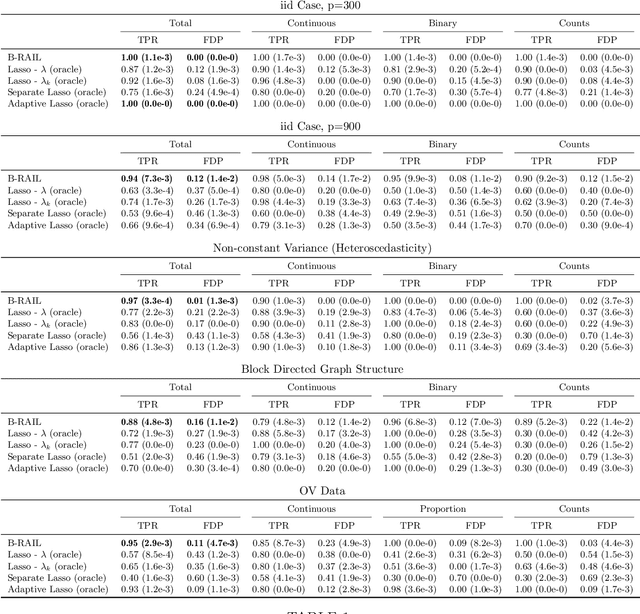
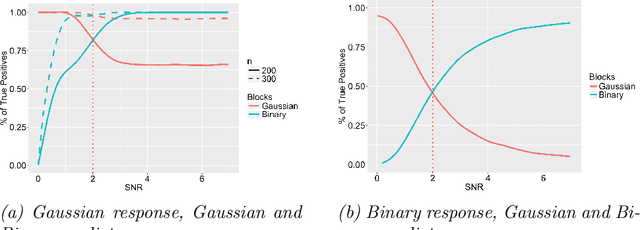
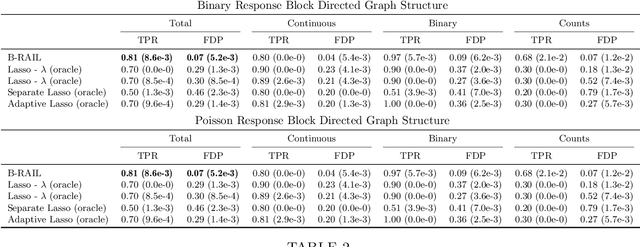
Data integration methods that analyze multiple sources of data simultaneously can often provide more holistic insights than can separate inquiries of each data source. Motivated by the advantages of data integration in the era of "big data", we investigate feature selection for high-dimensional multi-view data with mixed data types (e.g. continuous, binary, count-valued). This heterogeneity of multi-view data poses numerous challenges for existing feature selection methods. However, after critically examining these issues through empirical and theoretically-guided lenses, we develop a practical solution, the Block Randomized Adaptive Iterative Lasso (B-RAIL), which combines the strengths of the randomized Lasso, adaptive weighting schemes, and stability selection. B-RAIL serves as a versatile data integration method for sparse regression and graph selection, and we demonstrate the effectiveness of B-RAIL through extensive simulations and a case study to infer the ovarian cancer gene regulatory network. In this case study, B-RAIL successfully identifies well-known biomarkers associated with ovarian cancer and hints at novel candidates for future ovarian cancer research.