TabClustPFN: A Prior-Fitted Network for Tabular Data Clustering

Clustering tabular data is a fundamental yet challenging problem due to heterogeneous feature types, diverse data-generating mechanisms, and the absence of transferable inductive biases across datasets. Prior-fitted networks (PFNs) have recently demonstrated strong generalization in supervised tabular learning by amortizing Bayesian inference under a broad synthetic prior. Extending this paradigm to clustering is nontrivial: clustering is unsupervised, admits a combinatorial and permutation-invariant output space, and requires inferring the number of clusters. We introduce TabClustPFN, a prior-fitted network for tabular data clustering that performs amortized Bayesian inference over both cluster assignments and cluster cardinality. Pretrained on synthetic datasets drawn from a flexible clustering prior, TabClustPFN clusters unseen datasets in a single forward pass, without dataset-specific retraining or hyperparameter tuning. The model naturally handles heterogeneous numerical and categorical features and adapts to a wide range of clustering structures. Experiments on synthetic data and curated real-world tabular benchmarks show that TabClustPFN outperforms classical, deep, and amortized clustering baselines, while exhibiting strong robustness in out-of-the-box exploratory settings. Code is available at https://github.com/Tianqi-Zhao/TabClustPFN.

Human-AI Co-design for Clinical Prediction Models

Developing safe, effective, and practically useful clinical prediction models (CPMs) traditionally requires iterative collaboration between clinical experts, data scientists, and informaticists. This process refines the often small but critical details of the model building process, such as which features/patients to include and how clinical categories should be defined. However, this traditional collaboration process is extremely time- and resource-intensive, resulting in only a small fraction of CPMs reaching clinical practice. This challenge intensifies when teams attempt to incorporate unstructured clinical notes, which can contain an enormous number of concepts. To address this challenge, we introduce HACHI, an iterative human-in-the-loop framework that uses AI agents to accelerate the development of fully interpretable CPMs by enabling the exploration of concepts in clinical notes. HACHI alternates between (i) an AI agent rapidly exploring and evaluating candidate concepts in clinical notes and (ii) clinical and domain experts providing feedback to improve the CPM learning process. HACHI defines concepts as simple yes-no questions that are used in linear models, allowing the clinical AI team to transparently review, refine, and validate the CPM learned in each round. In two real-world prediction tasks (acute kidney injury and traumatic brain injury), HACHI outperforms existing approaches, surfaces new clinically relevant concepts not included in commonly-used CPMs, and improves model generalizability across clinical sites and time periods. Furthermore, HACHI reveals the critical role of the clinical AI team, such as directing the AI agent to explore concepts that it had not previously considered, adjusting the granularity of concepts it considers, changing the objective function to better align with the clinical objectives, and identifying issues of data bias and leakage.

Revisiting Randomization in Greedy Model Search

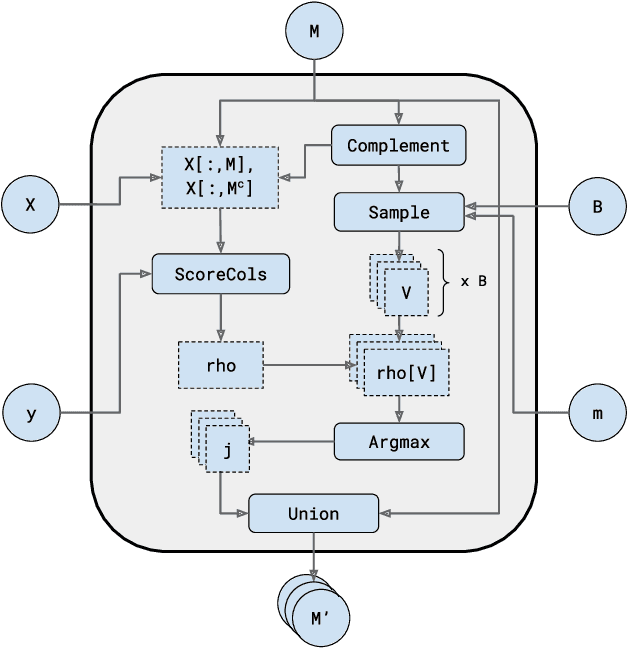
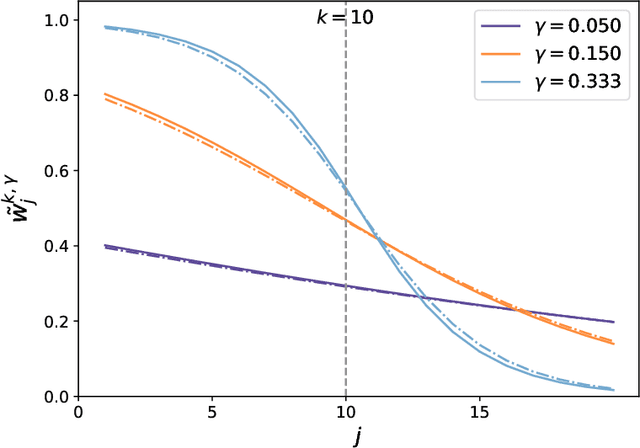
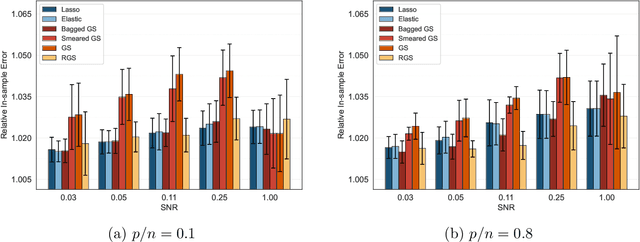
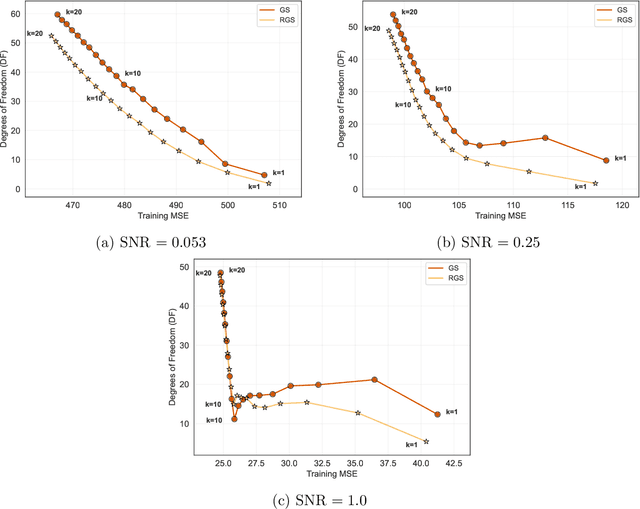
Combining randomized estimators in an ensemble, such as via random forests, has become a fundamental technique in modern data science, but can be computationally expensive. Furthermore, the mechanism by which this improves predictive performance is poorly understood. We address these issues in the context of sparse linear regression by proposing and analyzing an ensemble of greedy forward selection estimators that are randomized by feature subsampling -- at each iteration, the best feature is selected from within a random subset. We design a novel implementation based on dynamic programming that greatly improves its computational efficiency. Furthermore, we show via careful numerical experiments that our method can outperform popular methods such as lasso and elastic net across a wide range of settings. Next, contrary to prevailing belief that randomized ensembling is analogous to shrinkage, we show via numerical experiments that it can simultaneously reduce training error and degrees of freedom, thereby shifting the entire bias-variance trade-off curve of the base estimator. We prove this fact rigorously in the setting of orthogonal features, in which case, the ensemble estimator rescales the ordinary least squares coefficients with a two-parameter family of logistic weights, thereby enlarging the model search space. These results enhance our understanding of random forests and suggest that implicit regularization in general may have more complicated effects than explicit regularization.

TabPFN: One Model to Rule Them All?

Hollmann et al. (Nature 637 (2025) 319-326) recently introduced TabPFN, a transformer-based deep learning model for regression and classification on tabular data, which they claim "outperforms all previous methods on datasets with up to 10,000 samples by a wide margin, using substantially less training time." Furthermore, they have called TabPFN a "foundation model" for tabular data, as it can support "data generation, density estimation, learning reusable embeddings and fine-tuning". If these statements are well-supported, TabPFN may have the potential to supersede existing modeling approaches on a wide range of statistical tasks, mirroring a similar revolution in other areas of artificial intelligence that began with the advent of large language models. In this paper, we provide a tailored explanation of how TabPFN works for a statistics audience, by emphasizing its interpretation as approximate Bayesian inference. We also provide more evidence of TabPFN's "foundation model" capabilities: We show that an out-of-the-box application of TabPFN vastly outperforms specialized state-of-the-art methods for semi-supervised parameter estimation, prediction under covariate shift, and heterogeneous treatment effect estimation. We further show that TabPFN can outperform LASSO at sparse regression and can break a robustness-efficiency trade-off in classification. All experiments can be reproduced using the code provided at https://github.com/qinglong-tian/tabpfn_study (https://github.com/qinglong-tian/tabpfn_study).

Bayesian Concept Bottleneck Models with LLM Priors

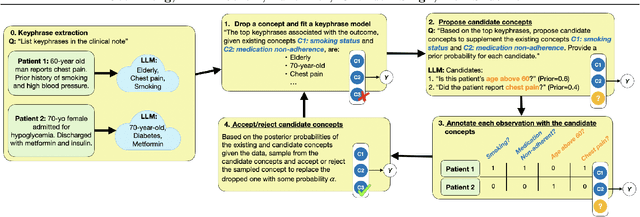
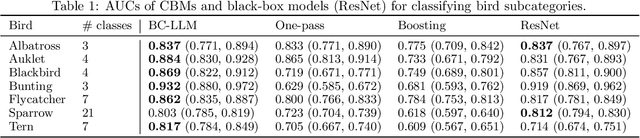
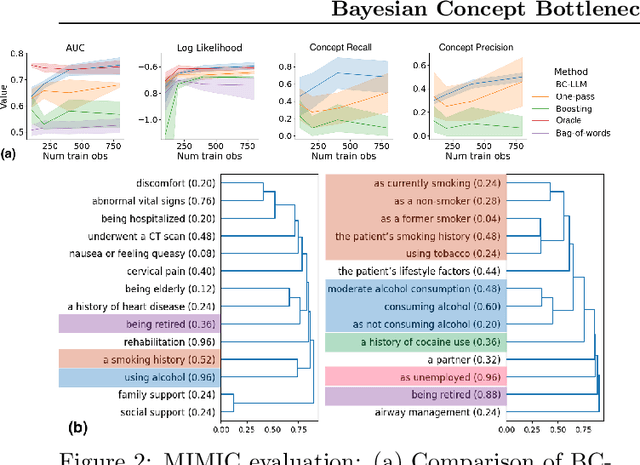
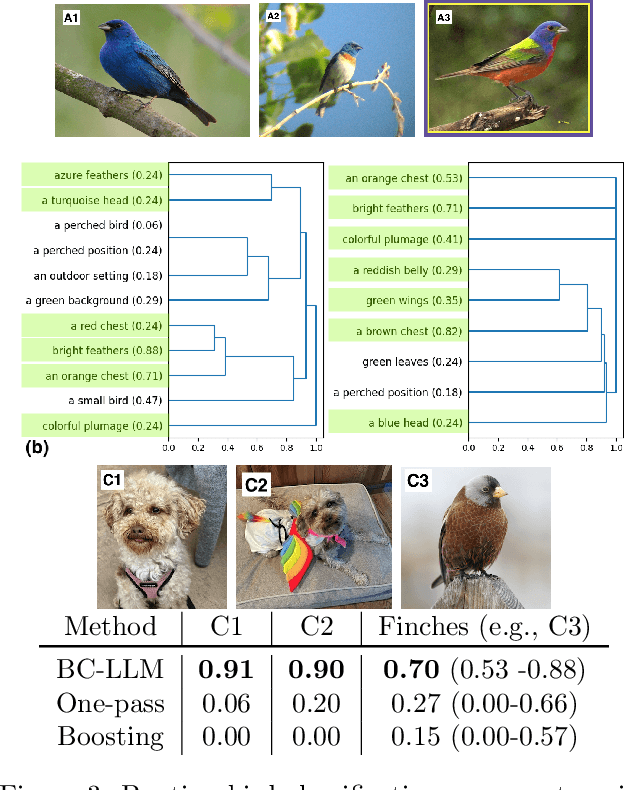
Concept Bottleneck Models (CBMs) have been proposed as a compromise between white-box and black-box models, aiming to achieve interpretability without sacrificing accuracy. The standard training procedure for CBMs is to predefine a candidate set of human-interpretable concepts, extract their values from the training data, and identify a sparse subset as inputs to a transparent prediction model. However, such approaches are often hampered by the tradeoff between enumerating a sufficiently large set of concepts to include those that are truly relevant versus controlling the cost of obtaining concept extractions. This work investigates a novel approach that sidesteps these challenges: BC-LLM iteratively searches over a potentially infinite set of concepts within a Bayesian framework, in which Large Language Models (LLMs) serve as both a concept extraction mechanism and prior. BC-LLM is broadly applicable and multi-modal. Despite imperfections in LLMs, we prove that BC-LLM can provide rigorous statistical inference and uncertainty quantification. In experiments, it outperforms comparator methods including black-box models, converges more rapidly towards relevant concepts and away from spuriously correlated ones, and is more robust to out-of-distribution samples.

The Computational Curse of Big Data for Bayesian Additive Regression Trees: A Hitting Time Analysis

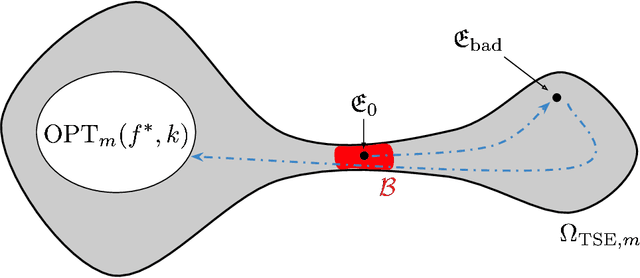
Bayesian Additive Regression Trees (BART) is a popular Bayesian non-parametric regression model that is commonly used in causal inference and beyond. Its strong predictive performance is supported by theoretical guarantees that its posterior distribution concentrates around the true regression function at optimal rates under various data generative settings and for appropriate prior choices. In this paper, we show that the BART sampler often converges slowly, confirming empirical observations by other researchers. Assuming discrete covariates, we show that, while the BART posterior concentrates on a set comprising all optimal tree structures (smallest bias and complexity), the Markov chain's hitting time for this set increases with $n$ (training sample size), under several common data generative settings. As $n$ increases, the approximate BART posterior thus becomes increasingly different from the exact posterior (for the same number of MCMC samples), contrasting with earlier concentration results on the exact posterior. This contrast is highlighted by our simulations showing worsening frequentist undercoverage for approximate posterior intervals and a growing ratio between the MSE of the approximate posterior and that obtainable by artificially improving convergence via averaging multiple sampler chains. Finally, based on our theoretical insights, possibilities are discussed to improve the BART sampler convergence performance.

Error Reduction from Stacked Regressions

Stacking regressions is an ensemble technique that forms linear combinations of different regression estimators to enhance predictive accuracy. The conventional approach uses cross-validation data to generate predictions from the constituent estimators, and least-squares with nonnegativity constraints to learn the combination weights. In this paper, we learn these weights analogously by minimizing an estimate of the population risk subject to a nonnegativity constraint. When the constituent estimators are linear least-squares projections onto nested subspaces separated by at least three dimensions, we show that thanks to a shrinkage effect, the resulting stacked estimator has strictly smaller population risk than best single estimator among them. Here "best" refers to an estimator that minimizes a model selection criterion such as AIC or BIC. In other words, in this setting, the best single estimator is inadmissible. Because the optimization problem can be reformulated as isotonic regression, the stacked estimator requires the same order of computation as the best single estimator, making it an attractive alternative in terms of both performance and implementation.

MDI+: A Flexible Random Forest-Based Feature Importance Framework

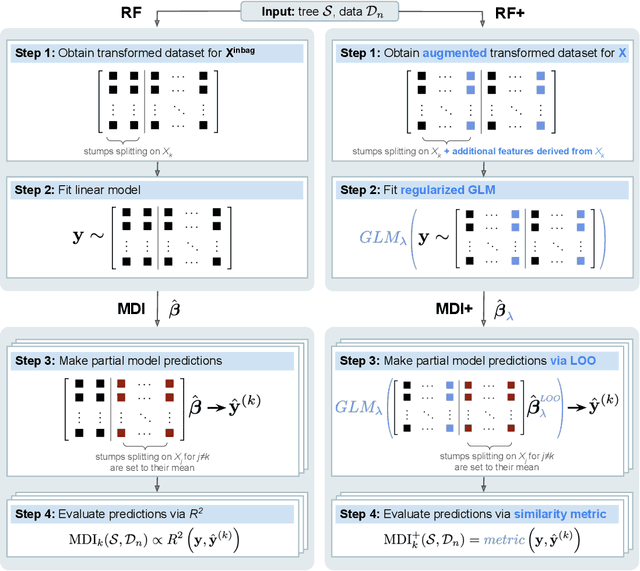
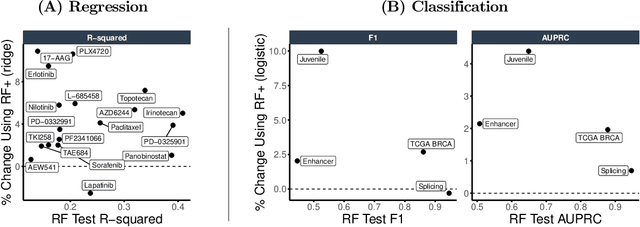
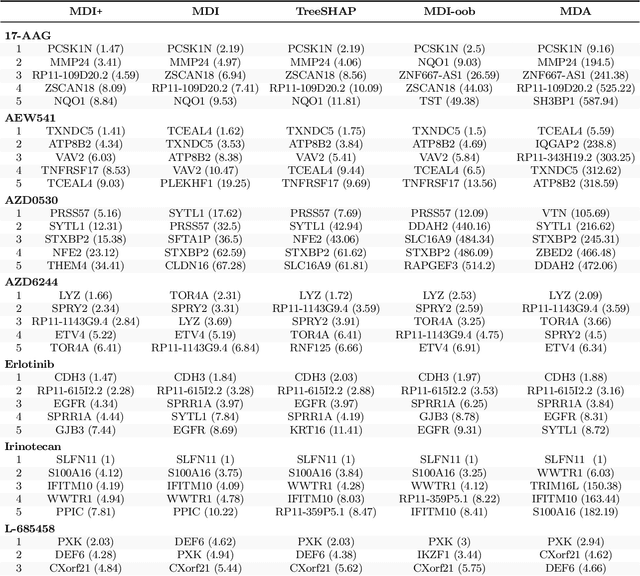
Mean decrease in impurity (MDI) is a popular feature importance measure for random forests (RFs). We show that the MDI for a feature $X_k$ in each tree in an RF is equivalent to the unnormalized $R^2$ value in a linear regression of the response on the collection of decision stumps that split on $X_k$. We use this interpretation to propose a flexible feature importance framework called MDI+. Specifically, MDI+ generalizes MDI by allowing the analyst to replace the linear regression model and $R^2$ metric with regularized generalized linear models (GLMs) and metrics better suited for the given data structure. Moreover, MDI+ incorporates additional features to mitigate known biases of decision trees against additive or smooth models. We further provide guidance on how practitioners can choose an appropriate GLM and metric based upon the Predictability, Computability, Stability framework for veridical data science. Extensive data-inspired simulations show that MDI+ significantly outperforms popular feature importance measures in identifying signal features. We also apply MDI+ to two real-world case studies on drug response prediction and breast cancer subtype classification. We show that MDI+ extracts well-established predictive genes with significantly greater stability compared to existing feature importance measures. All code and models are released in a full-fledged python package on Github.

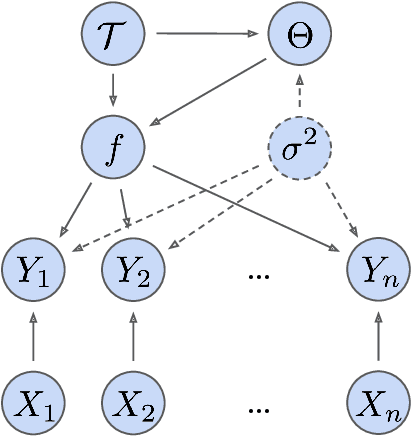
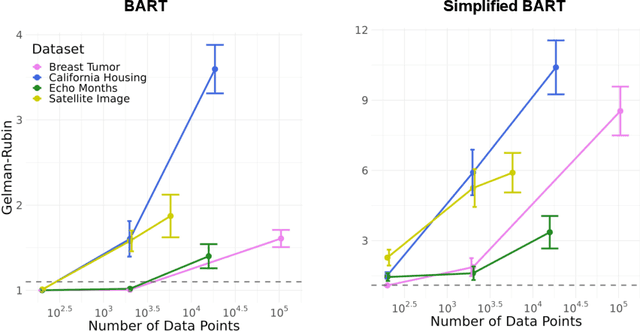
A Mixing Time Lower Bound for a Simplified Version of BART

Bayesian Additive Regression Trees (BART) is a popular Bayesian non-parametric regression algorithm. The posterior is a distribution over sums of decision trees, and predictions are made by averaging approximate samples from the posterior. The combination of strong predictive performance and the ability to provide uncertainty measures has led BART to be commonly used in the social sciences, biostatistics, and causal inference. BART uses Markov Chain Monte Carlo (MCMC) to obtain approximate posterior samples over a parameterized space of sums of trees, but it has often been observed that the chains are slow to mix. In this paper, we provide the first lower bound on the mixing time for a simplified version of BART in which we reduce the sum to a single tree and use a subset of the possible moves for the MCMC proposal distribution. Our lower bound for the mixing time grows exponentially with the number of data points. Inspired by this new connection between the mixing time and the number of data points, we perform rigorous simulations on BART. We show qualitatively that BART's mixing time increases with the number of data points. The slow mixing time of the simplified BART suggests a large variation between different runs of the simplified BART algorithm and a similar large variation is known for BART in the literature. This large variation could result in a lack of stability in the models, predictions, and posterior intervals obtained from the BART MCMC samples. Our lower bound and simulations suggest increasing the number of chains with the number of data points.

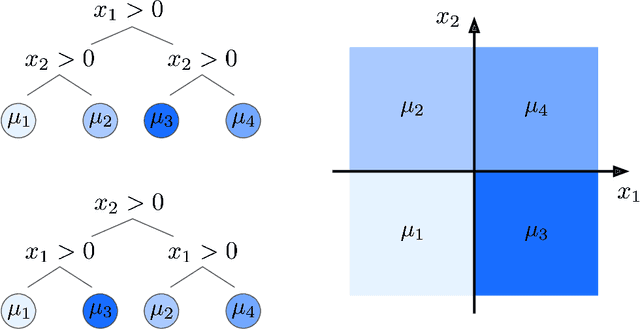
Fast Interpretable Greedy-Tree Sums (FIGS)

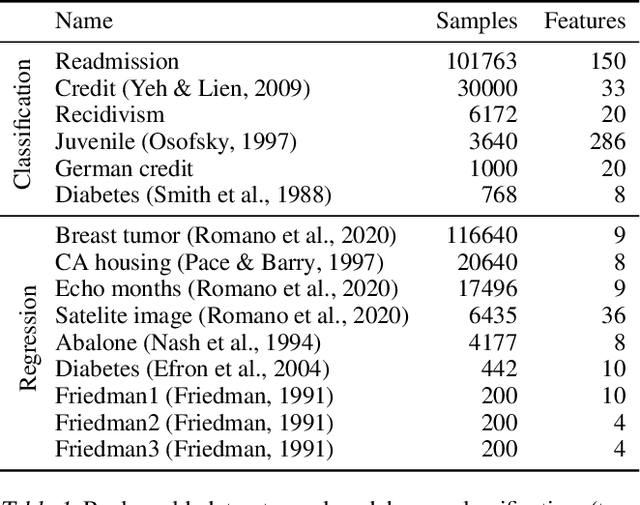
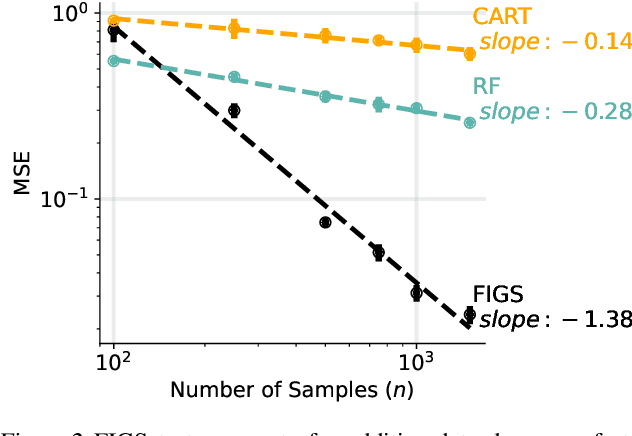
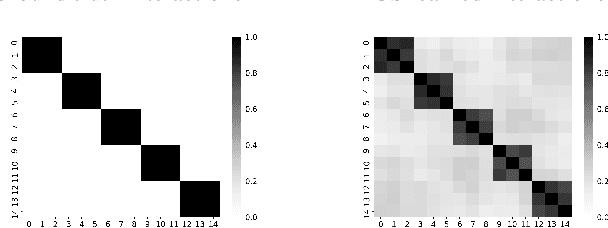
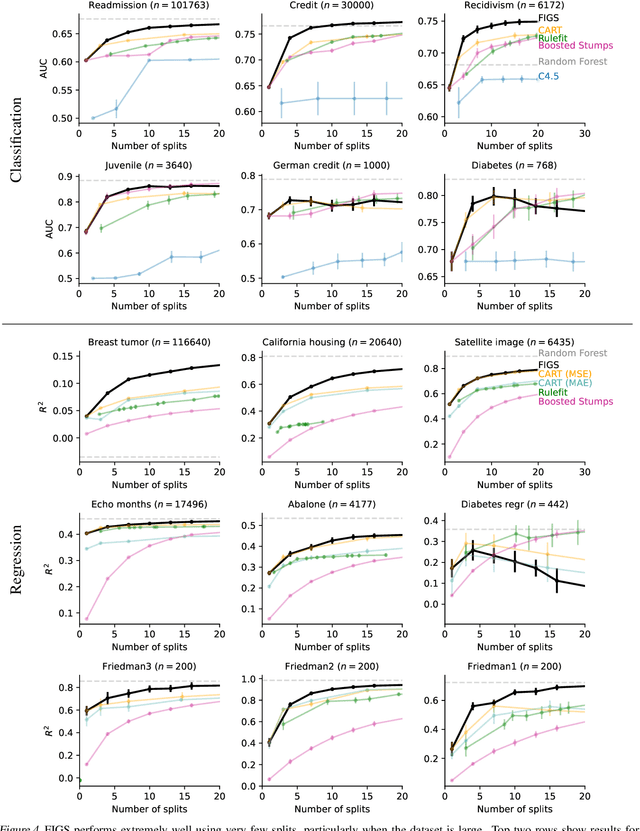
Modern machine learning has achieved impressive prediction performance, but often sacrifices interpretability, a critical consideration in many problems. Here, we propose Fast Interpretable Greedy-Tree Sums (FIGS), an algorithm for fitting concise rule-based models. Specifically, FIGS generalizes the CART algorithm to simultaneously grow a flexible number of trees in a summation. The total number of splits across all the trees can be restricted by a pre-specified threshold, thereby keeping both the size and number of its trees under control. When both are small, the fitted tree-sum can be easily visualized and written out by hand, making it highly interpretable. A partially oracle theoretical result hints at the potential for FIGS to overcome a key weakness of single-tree models by disentangling additive components of generative additive models, thereby reducing redundancy from repeated splits on the same feature. Furthermore, given oracle access to optimal tree structures, we obtain L2 generalization bounds for such generative models in the case of C1 component functions, matching known minimax rates in some cases. Extensive experiments across a wide array of real-world datasets show that FIGS achieves state-of-the-art prediction performance (among all popular rule-based methods) when restricted to just a few splits (e.g. less than 20). We find empirically that FIGS is able to avoid repeated splits, and often provides more concise decision rules than fitted decision trees, without sacrificing predictive performance. All code and models are released in a full-fledged package on Github \url{https://github.com/csinva/imodels}.