MDI+: A Flexible Random Forest-Based Feature Importance Framework
Paper and Code
Jul 04, 2023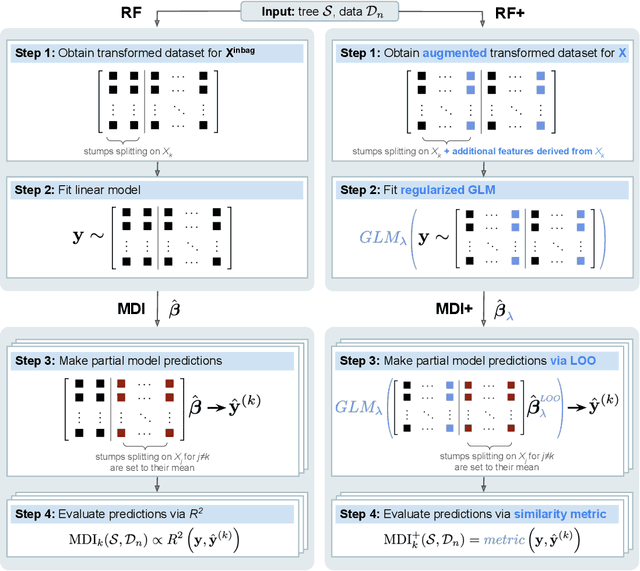

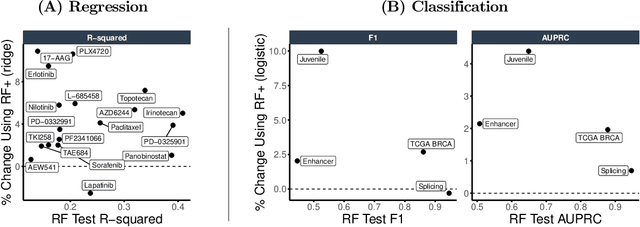
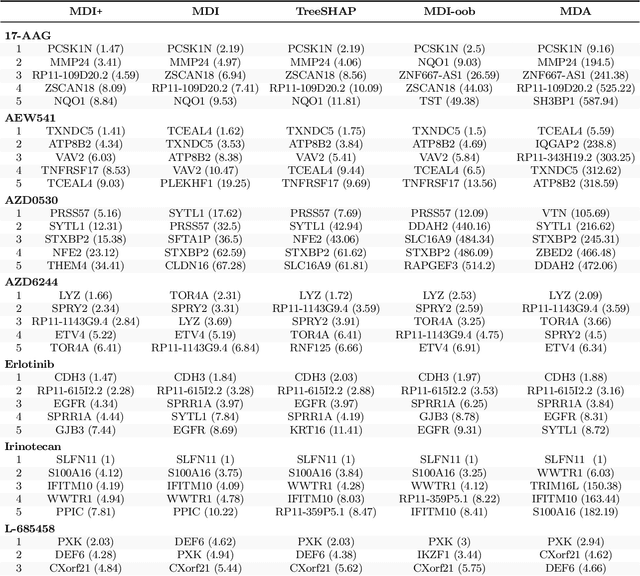
Mean decrease in impurity (MDI) is a popular feature importance measure for random forests (RFs). We show that the MDI for a feature $X_k$ in each tree in an RF is equivalent to the unnormalized $R^2$ value in a linear regression of the response on the collection of decision stumps that split on $X_k$. We use this interpretation to propose a flexible feature importance framework called MDI+. Specifically, MDI+ generalizes MDI by allowing the analyst to replace the linear regression model and $R^2$ metric with regularized generalized linear models (GLMs) and metrics better suited for the given data structure. Moreover, MDI+ incorporates additional features to mitigate known biases of decision trees against additive or smooth models. We further provide guidance on how practitioners can choose an appropriate GLM and metric based upon the Predictability, Computability, Stability framework for veridical data science. Extensive data-inspired simulations show that MDI+ significantly outperforms popular feature importance measures in identifying signal features. We also apply MDI+ to two real-world case studies on drug response prediction and breast cancer subtype classification. We show that MDI+ extracts well-established predictive genes with significantly greater stability compared to existing feature importance measures. All code and models are released in a full-fledged python package on Github.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge