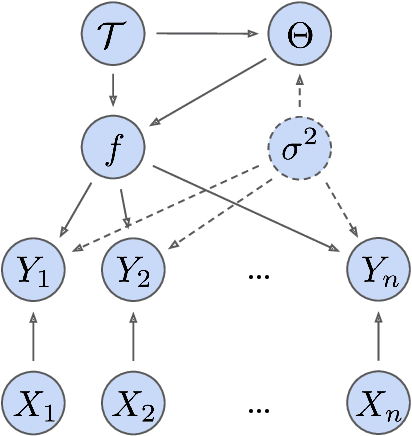
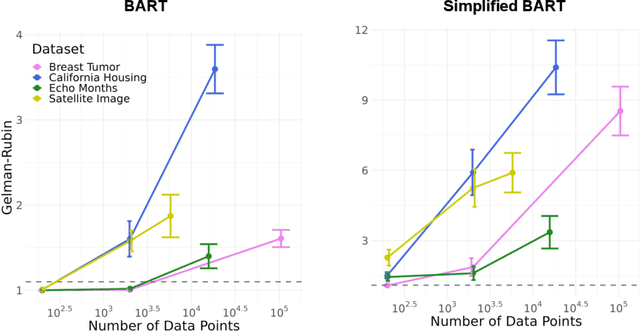
The Computational Curse of Big Data for Bayesian Additive Regression Trees: A Hitting Time Analysis

Bayesian Additive Regression Trees (BART) is a popular Bayesian non-parametric regression model that is commonly used in causal inference and beyond. Its strong predictive performance is supported by theoretical guarantees that its posterior distribution concentrates around the true regression function at optimal rates under various data generative settings and for appropriate prior choices. In this paper, we show that the BART sampler often converges slowly, confirming empirical observations by other researchers. Assuming discrete covariates, we show that, while the BART posterior concentrates on a set comprising all optimal tree structures (smallest bias and complexity), the Markov chain's hitting time for this set increases with $n$ (training sample size), under several common data generative settings. As $n$ increases, the approximate BART posterior thus becomes increasingly different from the exact posterior (for the same number of MCMC samples), contrasting with earlier concentration results on the exact posterior. This contrast is highlighted by our simulations showing worsening frequentist undercoverage for approximate posterior intervals and a growing ratio between the MSE of the approximate posterior and that obtainable by artificially improving convergence via averaging multiple sampler chains. Finally, based on our theoretical insights, possibilities are discussed to improve the BART sampler convergence performance.

Assessing the Usability of GutGPT: A Simulation Study of an AI Clinical Decision Support System for Gastrointestinal Bleeding Risk

Applications of large language models (LLMs) like ChatGPT have potential to enhance clinical decision support through conversational interfaces. However, challenges of human-algorithmic interaction and clinician trust are poorly understood. GutGPT, a LLM for gastrointestinal (GI) bleeding risk prediction and management guidance, was deployed in clinical simulation scenarios alongside the electronic health record (EHR) with emergency medicine physicians, internal medicine physicians, and medical students to evaluate its effect on physician acceptance and trust in AI clinical decision support systems (AI-CDSS). GutGPT provides risk predictions from a validated machine learning model and evidence-based answers by querying extracted clinical guidelines. Participants were randomized to GutGPT and an interactive dashboard, or the interactive dashboard and a search engine. Surveys and educational assessments taken before and after measured technology acceptance and content mastery. Preliminary results showed mixed effects on acceptance after using GutGPT compared to the dashboard or search engine but appeared to improve content mastery based on simulation performance. Overall, this study demonstrates LLMs like GutGPT could enhance effective AI-CDSS if implemented optimally and paired with interactive interfaces.

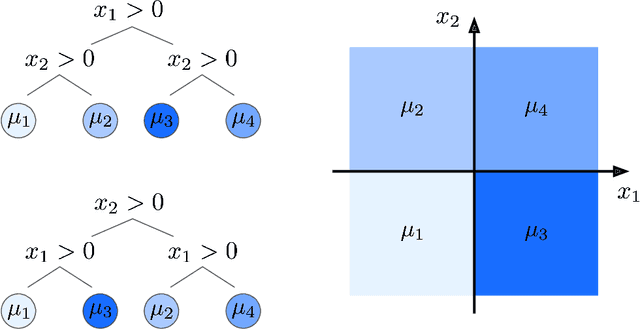
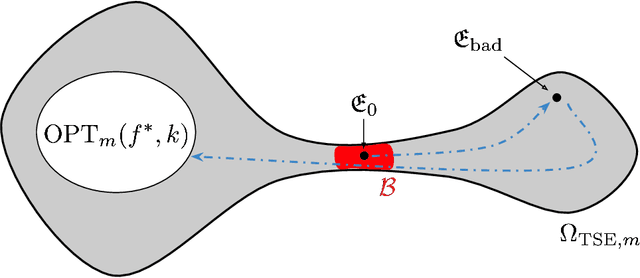
A Mixing Time Lower Bound for a Simplified Version of BART

Bayesian Additive Regression Trees (BART) is a popular Bayesian non-parametric regression algorithm. The posterior is a distribution over sums of decision trees, and predictions are made by averaging approximate samples from the posterior. The combination of strong predictive performance and the ability to provide uncertainty measures has led BART to be commonly used in the social sciences, biostatistics, and causal inference. BART uses Markov Chain Monte Carlo (MCMC) to obtain approximate posterior samples over a parameterized space of sums of trees, but it has often been observed that the chains are slow to mix. In this paper, we provide the first lower bound on the mixing time for a simplified version of BART in which we reduce the sum to a single tree and use a subset of the possible moves for the MCMC proposal distribution. Our lower bound for the mixing time grows exponentially with the number of data points. Inspired by this new connection between the mixing time and the number of data points, we perform rigorous simulations on BART. We show qualitatively that BART's mixing time increases with the number of data points. The slow mixing time of the simplified BART suggests a large variation between different runs of the simplified BART algorithm and a similar large variation is known for BART in the literature. This large variation could result in a lack of stability in the models, predictions, and posterior intervals obtained from the BART MCMC samples. Our lower bound and simulations suggest increasing the number of chains with the number of data points.