The Computational Curse of Big Data for Bayesian Additive Regression Trees: A Hitting Time Analysis
Paper and Code
Jun 28, 2024
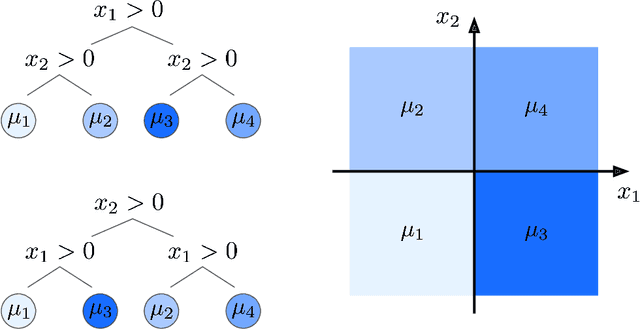
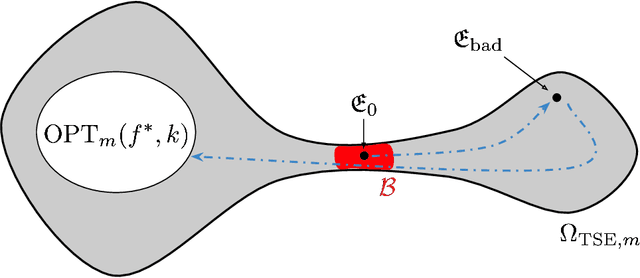

Bayesian Additive Regression Trees (BART) is a popular Bayesian non-parametric regression model that is commonly used in causal inference and beyond. Its strong predictive performance is supported by theoretical guarantees that its posterior distribution concentrates around the true regression function at optimal rates under various data generative settings and for appropriate prior choices. In this paper, we show that the BART sampler often converges slowly, confirming empirical observations by other researchers. Assuming discrete covariates, we show that, while the BART posterior concentrates on a set comprising all optimal tree structures (smallest bias and complexity), the Markov chain's hitting time for this set increases with $n$ (training sample size), under several common data generative settings. As $n$ increases, the approximate BART posterior thus becomes increasingly different from the exact posterior (for the same number of MCMC samples), contrasting with earlier concentration results on the exact posterior. This contrast is highlighted by our simulations showing worsening frequentist undercoverage for approximate posterior intervals and a growing ratio between the MSE of the approximate posterior and that obtainable by artificially improving convergence via averaging multiple sampler chains. Finally, based on our theoretical insights, possibilities are discussed to improve the BART sampler convergence performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge