Revisiting Randomization in Greedy Model Search

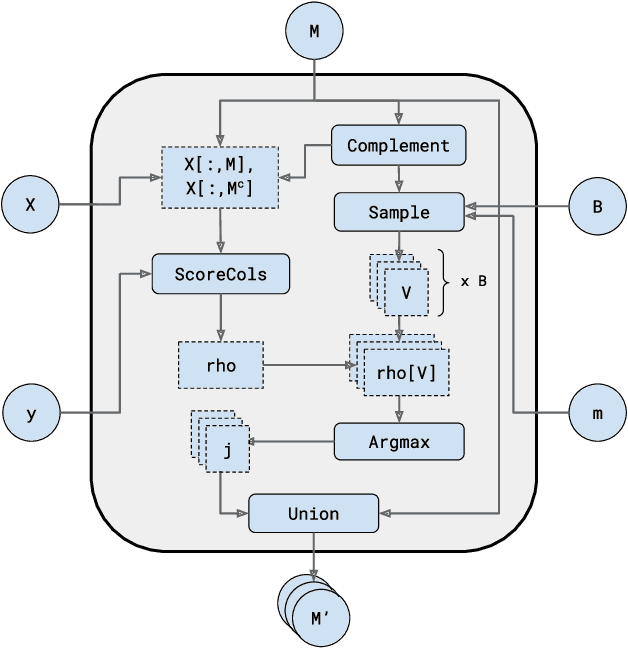
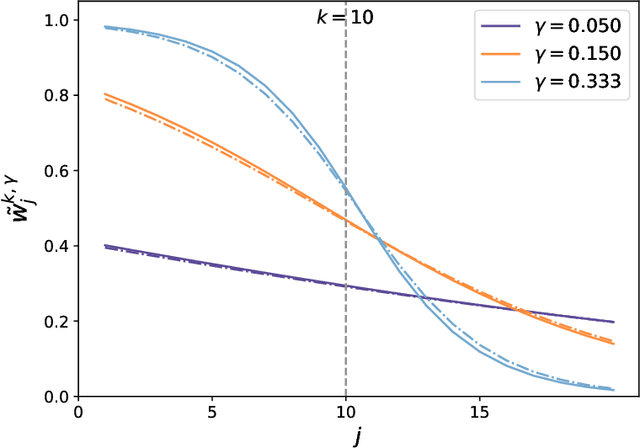
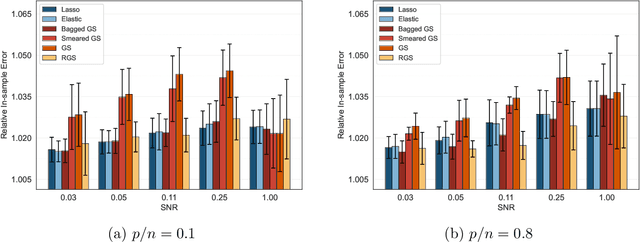
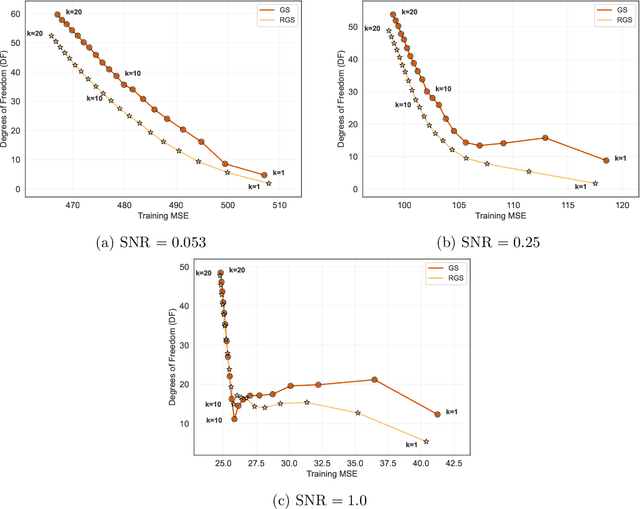
Combining randomized estimators in an ensemble, such as via random forests, has become a fundamental technique in modern data science, but can be computationally expensive. Furthermore, the mechanism by which this improves predictive performance is poorly understood. We address these issues in the context of sparse linear regression by proposing and analyzing an ensemble of greedy forward selection estimators that are randomized by feature subsampling -- at each iteration, the best feature is selected from within a random subset. We design a novel implementation based on dynamic programming that greatly improves its computational efficiency. Furthermore, we show via careful numerical experiments that our method can outperform popular methods such as lasso and elastic net across a wide range of settings. Next, contrary to prevailing belief that randomized ensembling is analogous to shrinkage, we show via numerical experiments that it can simultaneously reduce training error and degrees of freedom, thereby shifting the entire bias-variance trade-off curve of the base estimator. We prove this fact rigorously in the setting of orthogonal features, in which case, the ensemble estimator rescales the ordinary least squares coefficients with a two-parameter family of logistic weights, thereby enlarging the model search space. These results enhance our understanding of random forests and suggest that implicit regularization in general may have more complicated effects than explicit regularization.

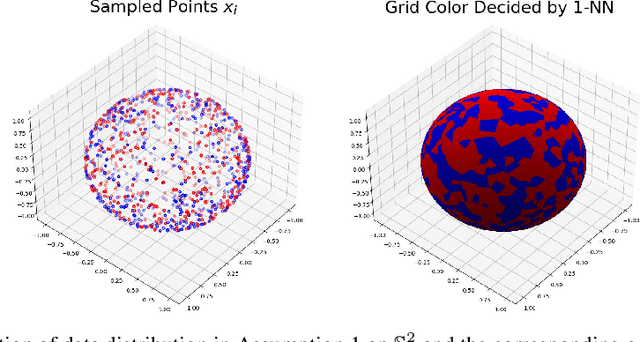
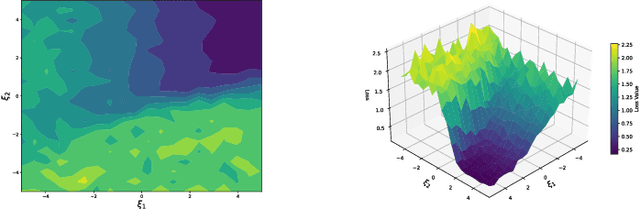
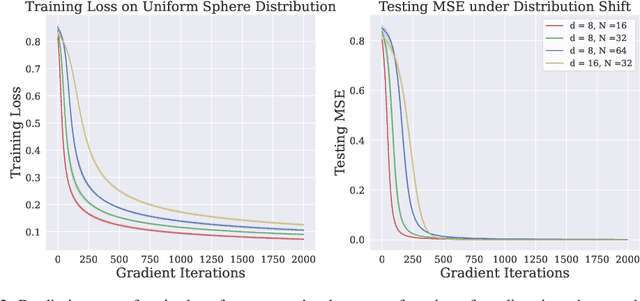
One-Layer Transformer Provably Learns One-Nearest Neighbor In Context

Transformers have achieved great success in recent years. Interestingly, transformers have shown particularly strong in-context learning capability -- even without fine-tuning, they are still able to solve unseen tasks well purely based on task-specific prompts. In this paper, we study the capability of one-layer transformers in learning one of the most classical nonparametric estimators, the one-nearest neighbor prediction rule. Under a theoretical framework where the prompt contains a sequence of labeled training data and unlabeled test data, we show that, although the loss function is nonconvex when trained with gradient descent, a single softmax attention layer can successfully learn to behave like a one-nearest neighbor classifier. Our result gives a concrete example of how transformers can be trained to implement nonparametric machine learning algorithms, and sheds light on the role of softmax attention in transformer models.

Decoding Game: On Minimax Optimality of Heuristic Text Generation Strategies

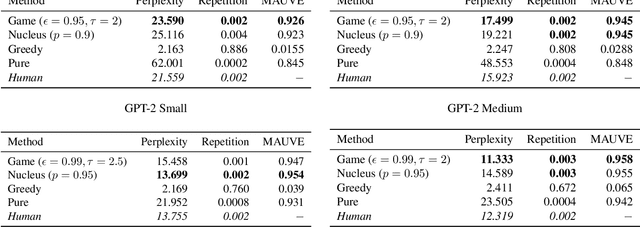
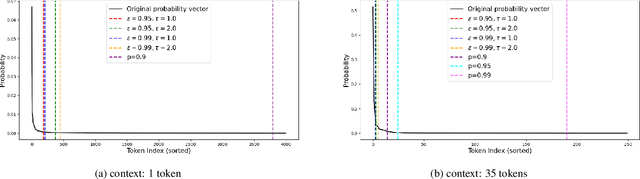
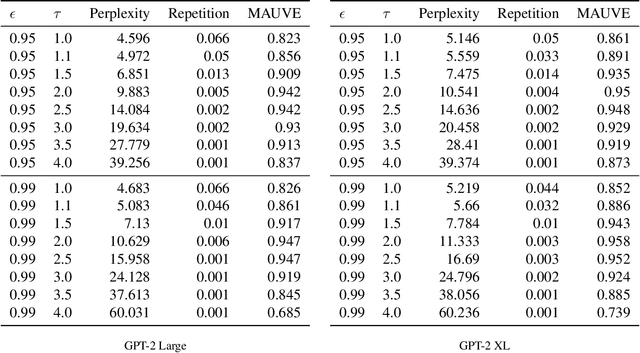
Decoding strategies play a pivotal role in text generation for modern language models, yet a puzzling gap divides theory and practice. Surprisingly, strategies that should intuitively be optimal, such as Maximum a Posteriori (MAP), often perform poorly in practice. Meanwhile, popular heuristic approaches like Top-$k$ and Nucleus sampling, which employ truncation and normalization of the conditional next-token probabilities, have achieved great empirical success but lack theoretical justifications. In this paper, we propose Decoding Game, a comprehensive theoretical framework which reimagines text generation as a two-player zero-sum game between Strategist, who seeks to produce text credible in the true distribution, and Nature, who distorts the true distribution adversarially. After discussing the decomposibility of multi-step generation, we derive the optimal strategy in closed form for one-step Decoding Game. It is shown that the adversarial Nature imposes an implicit regularization on likelihood maximization, and truncation-normalization methods are first-order approximations to the optimal strategy under this regularization. Additionally, by generalizing the objective and parameters of Decoding Game, near-optimal strategies encompass diverse methods such as greedy search, temperature scaling, and hybrids thereof. Numerical experiments are conducted to complement our theoretical analysis.

Challenges in Variable Importance Ranking Under Correlation

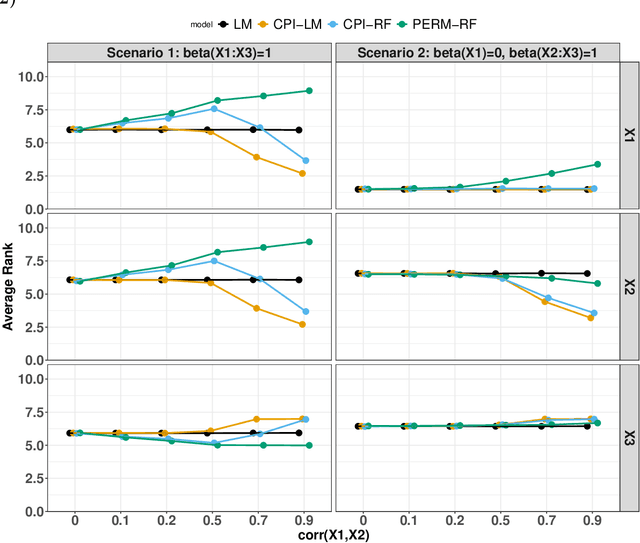
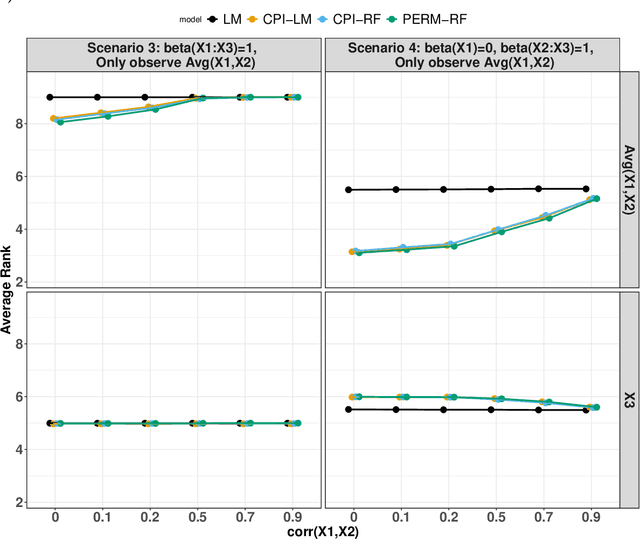
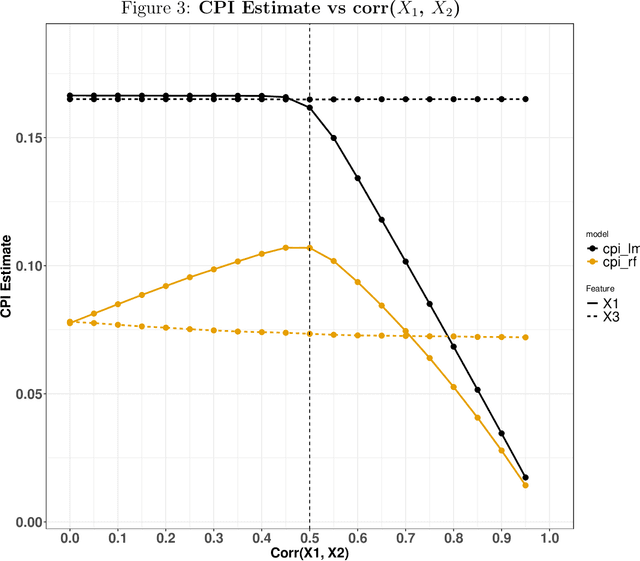
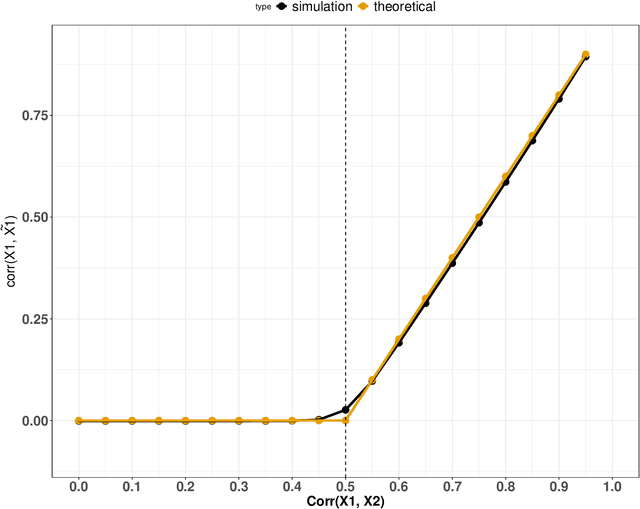
Variable importance plays a pivotal role in interpretable machine learning as it helps measure the impact of factors on the output of the prediction model. Model agnostic methods based on the generation of "null" features via permutation (or related approaches) can be applied. Such analysis is often utilized in pharmaceutical applications due to its ability to interpret black-box models, including tree-based ensembles. A major challenge and significant confounder in variable importance estimation however is the presence of between-feature correlation. Recently, several adjustments to marginal permutation utilizing feature knockoffs were proposed to address this issue, such as the variable importance measure known as conditional predictive impact (CPI). Assessment and evaluation of such approaches is the focus of our work. We first present a comprehensive simulation study investigating the impact of feature correlation on the assessment of variable importance. We then theoretically prove the limitation that highly correlated features pose for the CPI through the knockoff construction. While we expect that there is always no correlation between knockoff variables and its corresponding predictor variables, we prove that the correlation increases linearly beyond a certain correlation threshold between the predictor variables. Our findings emphasize the absence of free lunch when dealing with high feature correlation, as well as the necessity of understanding the utility and limitations behind methods in variable importance estimation.

Stochastic Gradient Descent for Additive Nonparametric Regression

This paper introduces an iterative algorithm designed to train additive models with favorable memory storage and computational requirements. The algorithm can be viewed as the functional counterpart of stochastic gradient descent, applied to the coefficients of a truncated basis expansion of the component functions. We show that the resulting estimator satisfies an oracle inequality that allows for model mispecification. In the well-specified setting, by choosing the learning rate carefully across three distinct stages of training, we prove that its risk is minimax optimal in terms of the dependence on the dimensionality of the data and the size of the training sample.

Inference with Mondrian Random Forests

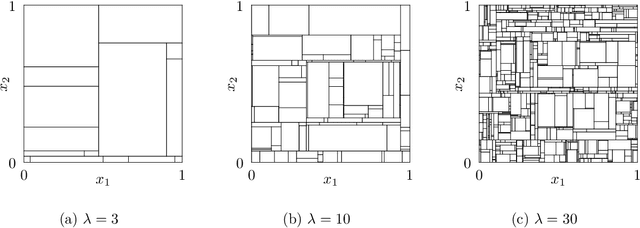
Random forests are popular methods for classification and regression, and many different variants have been proposed in recent years. One interesting example is the Mondrian random forest, in which the underlying trees are constructed according to a Mondrian process. In this paper we give a central limit theorem for the estimates made by a Mondrian random forest in the regression setting. When combined with a bias characterization and a consistent variance estimator, this allows one to perform asymptotically valid statistical inference, such as constructing confidence intervals, on the unknown regression function. We also provide a debiasing procedure for Mondrian random forests which allows them to achieve minimax-optimal estimation rates with $\beta$-H\"older regression functions, for all $\beta$ and in arbitrary dimension, assuming appropriate parameter tuning.

Robust Transfer Learning with Unreliable Source Data

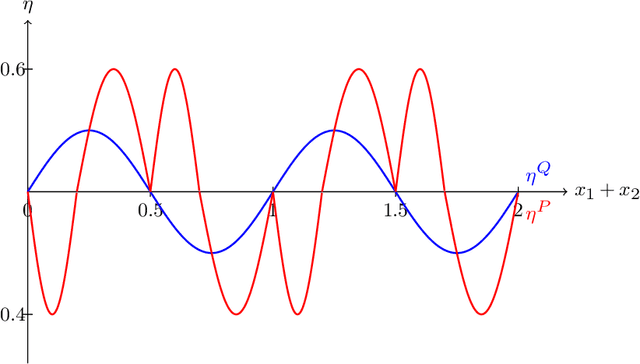
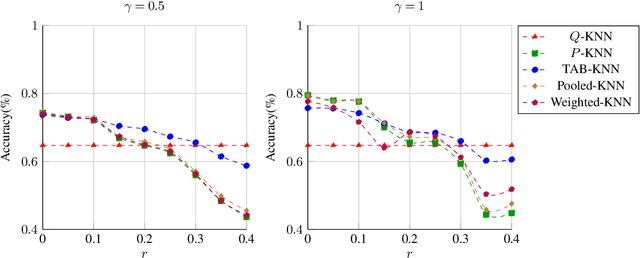
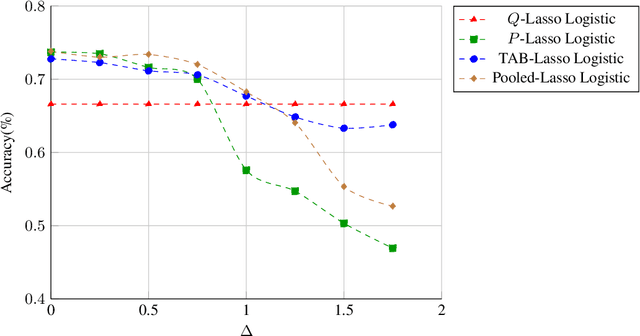
This paper addresses challenges in robust transfer learning stemming from ambiguity in Bayes classifiers and weak transferable signals between the target and source distribution. We introduce a novel quantity called the ''ambiguity level'' that measures the discrepancy between the target and source regression functions, propose a simple transfer learning procedure, and establish a general theorem that shows how this new quantity is related to the transferability of learning in terms of risk improvements. Our proposed ''Transfer Around Boundary'' (TAB) model, with a threshold balancing the performance of target and source data, is shown to be both efficient and robust, improving classification while avoiding negative transfer. Moreover, we demonstrate the effectiveness of the TAB model on non-parametric classification and logistic regression tasks, achieving upper bounds which are optimal up to logarithmic factors. Simulation studies lend further support to the effectiveness of TAB. We also provide simple approaches to bound the excess misclassification error without the need for specialized knowledge in transfer learning.

Error Reduction from Stacked Regressions

Stacking regressions is an ensemble technique that forms linear combinations of different regression estimators to enhance predictive accuracy. The conventional approach uses cross-validation data to generate predictions from the constituent estimators, and least-squares with nonnegativity constraints to learn the combination weights. In this paper, we learn these weights analogously by minimizing an estimate of the population risk subject to a nonnegativity constraint. When the constituent estimators are linear least-squares projections onto nested subspaces separated by at least three dimensions, we show that thanks to a shrinkage effect, the resulting stacked estimator has strictly smaller population risk than best single estimator among them. Here "best" refers to an estimator that minimizes a model selection criterion such as AIC or BIC. In other words, in this setting, the best single estimator is inadmissible. Because the optimization problem can be reformulated as isotonic regression, the stacked estimator requires the same order of computation as the best single estimator, making it an attractive alternative in terms of both performance and implementation.

On the Implicit Bias of Adam

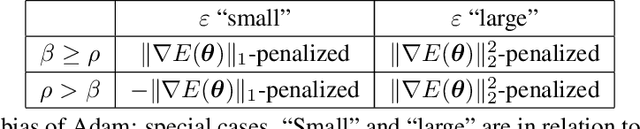
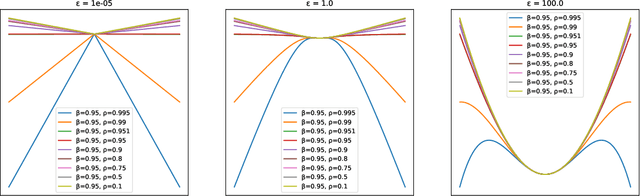
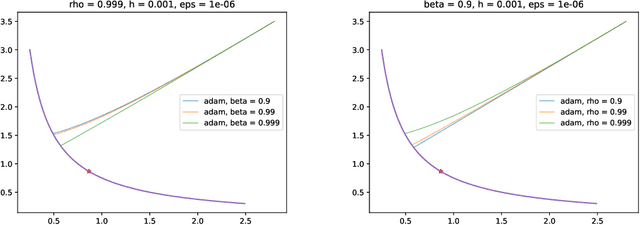
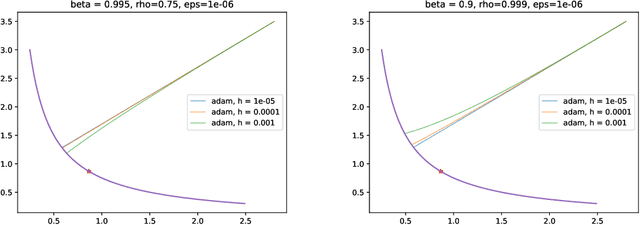
In previous literature, backward error analysis was used to find ordinary differential equations (ODEs) approximating the gradient descent trajectory. It was found that finite step sizes implicitly regularize solutions because terms appearing in the ODEs penalize the two-norm of the loss gradients. We prove that the existence of similar implicit regularization in RMSProp and Adam depends on their hyperparameters and the training stage, but with a different "norm" involved: the corresponding ODE terms either penalize the (perturbed) one-norm of the loss gradients or, on the contrary, hinder its decrease (the latter case being typical). We also conduct numerical experiments and discuss how the proven facts can influence generalization.

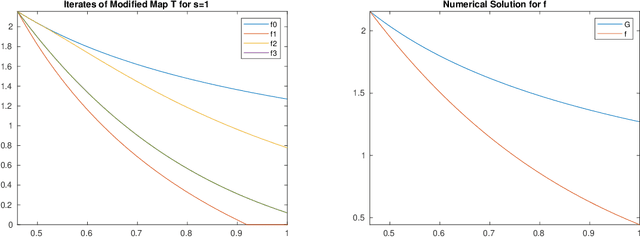
Sharp Convergence Rates for Matching Pursuit

We study the fundamental limits of matching pursuit, or the pure greedy algorithm, for approximating a target function by a sparse linear combination of elements from a dictionary. When the target function is contained in the variation space corresponding to the dictionary, many impressive works over the past few decades have obtained upper and lower bounds on the error of matching pursuit, but they do not match. The main contribution of this paper is to close this gap and obtain a sharp characterization of the decay rate of matching pursuit. Specifically, we construct a worst case dictionary which shows that the existing best upper bound cannot be significantly improved. It turns out that, unlike other greedy algorithm variants, the converge rate is suboptimal and is determined by the solution to a certain non-linear equation. This enables us to conclude that any amount of shrinkage improves matching pursuit in the worst case.