Challenges in Variable Importance Ranking Under Correlation

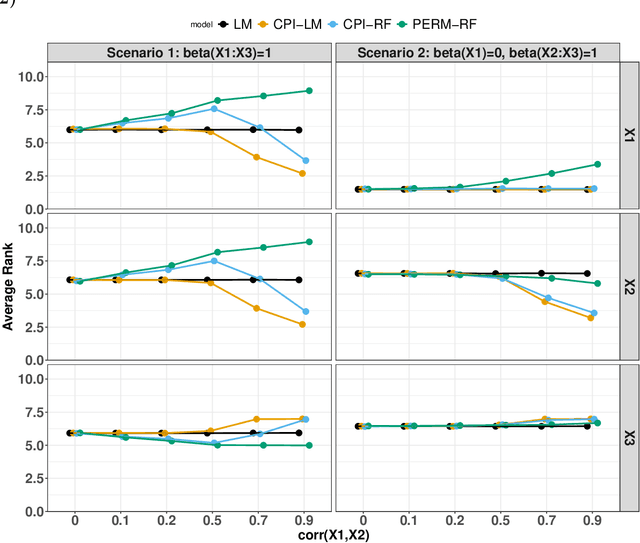
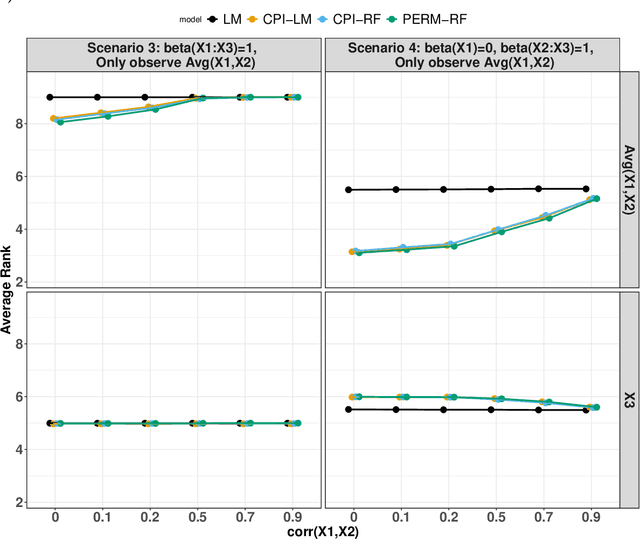
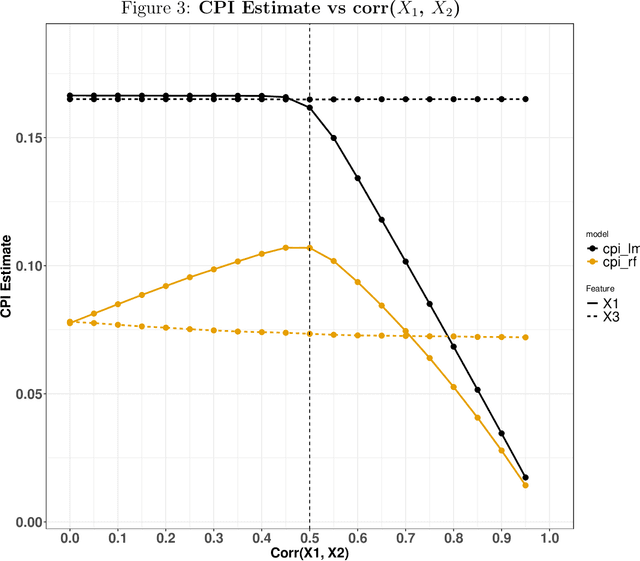
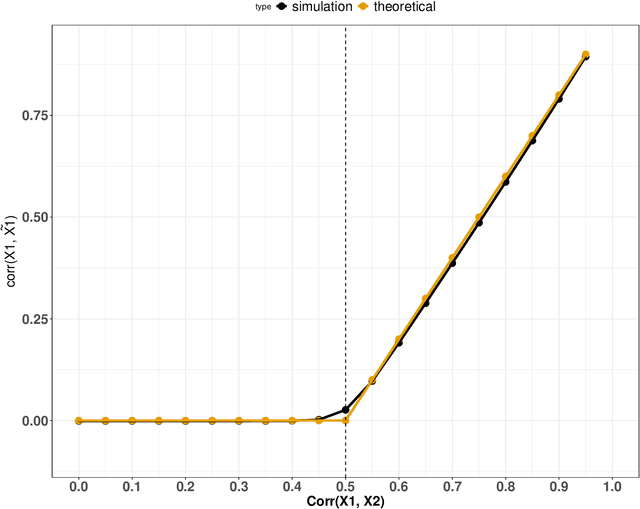
Variable importance plays a pivotal role in interpretable machine learning as it helps measure the impact of factors on the output of the prediction model. Model agnostic methods based on the generation of "null" features via permutation (or related approaches) can be applied. Such analysis is often utilized in pharmaceutical applications due to its ability to interpret black-box models, including tree-based ensembles. A major challenge and significant confounder in variable importance estimation however is the presence of between-feature correlation. Recently, several adjustments to marginal permutation utilizing feature knockoffs were proposed to address this issue, such as the variable importance measure known as conditional predictive impact (CPI). Assessment and evaluation of such approaches is the focus of our work. We first present a comprehensive simulation study investigating the impact of feature correlation on the assessment of variable importance. We then theoretically prove the limitation that highly correlated features pose for the CPI through the knockoff construction. While we expect that there is always no correlation between knockoff variables and its corresponding predictor variables, we prove that the correlation increases linearly beyond a certain correlation threshold between the predictor variables. Our findings emphasize the absence of free lunch when dealing with high feature correlation, as well as the necessity of understanding the utility and limitations behind methods in variable importance estimation.

Measuring the Completeness of Theories

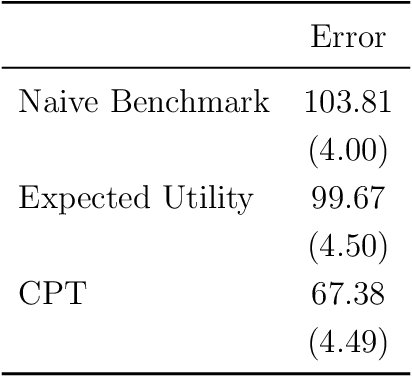
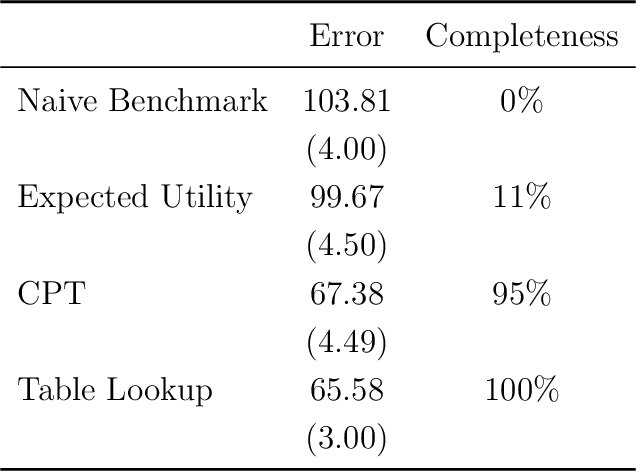
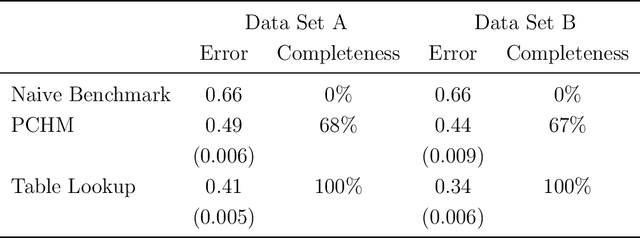
We use machine learning to provide a tractable measure of the amount of predictable variation in the data that a theory captures, which we call its "completeness." We apply this measure to three problems: assigning certain equivalents to lotteries, initial play in games, and human generation of random sequences. We discover considerable variation in the completeness of existing models, which sheds light on whether to focus on developing better models with the same features or instead to look for new features that will improve predictions. We also illustrate how and why completeness varies with the experiments considered, which highlights the role played in choosing which experiments to run.

Overabundant Information and Learning Traps

We develop a model of social learning from overabundant information: Short-lived agents sequentially choose from a large set of (flexibly correlated) information sources for prediction of an unknown state. Signal realizations are public. We demonstrate two starkly different long-run outcomes: (1) efficient information aggregation, where the community eventually learns as fast as possible; (2) "learning traps," where the community gets stuck observing suboptimal sources and learns inefficiently. Our main results identify a simple property of the signal correlation structure that separates these outcomes. In both regimes, we characterize which sources are observed in the long run and how often.

Optimal and Myopic Information Acquisition

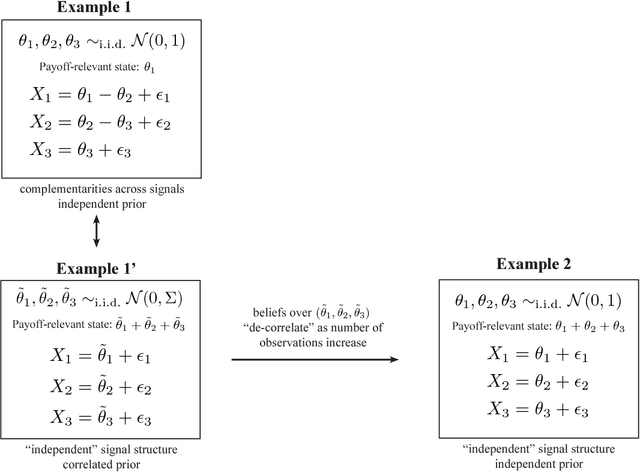
We consider the problem of optimal dynamic information acquisition from many correlated information sources. Each period, the decision-maker jointly takes an action and allocates a fixed number of observations across the available sources. His payoff depends on the actions taken and on an unknown state. In the canonical setting of jointly normal information sources, we show that the optimal dynamic information acquisition rule proceeds myopically after finitely many periods. If signals are acquired in large blocks each period, then the optimal rule turns out to be myopic from period 1. These results demonstrate the possibility of robust and "simple" optimal information acquisition, and simplify the analysis of dynamic information acquisition in a widely used informational environment.

The Theory is Predictive, but is it Complete? An Application to Human Perception of Randomness

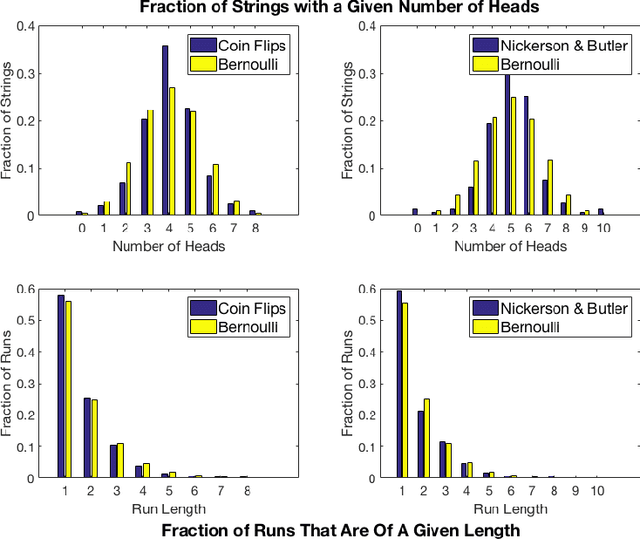
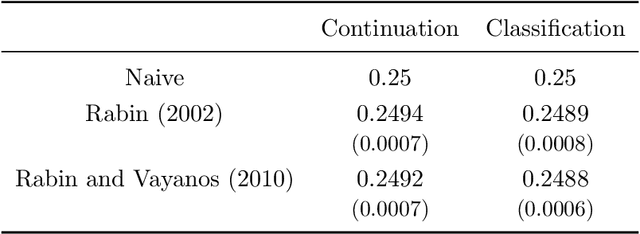
When we test a theory using data, it is common to focus on correctness: do the predictions of the theory match what we see in the data? But we also care about completeness: how much of the predictable variation in the data is captured by the theory? This question is difficult to answer, because in general we do not know how much "predictable variation" there is in the problem. In this paper, we consider approaches motivated by machine learning algorithms as a means of constructing a benchmark for the best attainable level of prediction. We illustrate our methods on the task of predicting human-generated random sequences. Relative to an atheoretical machine learning algorithm benchmark, we find that existing behavioral models explain roughly 15 percent of the predictable variation in this problem. This fraction is robust across several variations on the problem. We also consider a version of this approach for analyzing field data from domains in which human perception and generation of randomness has been used as a conceptual framework; these include sequential decision-making and repeated zero-sum games. In these domains, our framework for testing the completeness of theories provides a way of assessing their effectiveness over different contexts; we find that despite some differences, the existing theories are fairly stable across our field domains in their performance relative to the benchmark. Overall, our results indicate that (i) there is a significant amount of structure in this problem that existing models have yet to capture and (ii) there are rich domains in which machine learning may provide a viable approach to testing completeness.