Challenges in Variable Importance Ranking Under Correlation

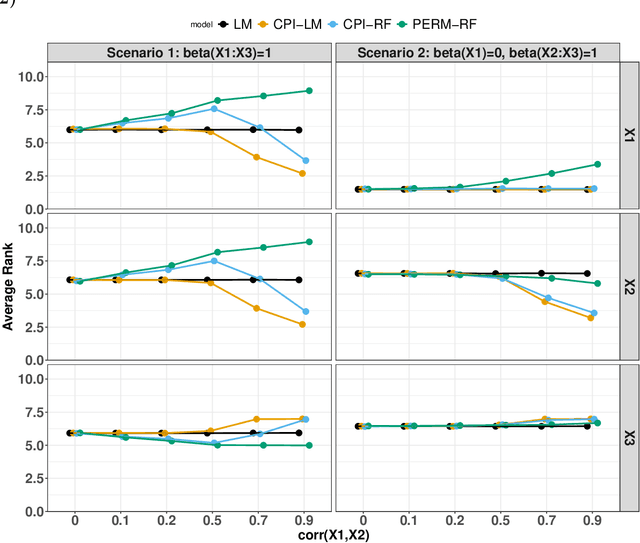
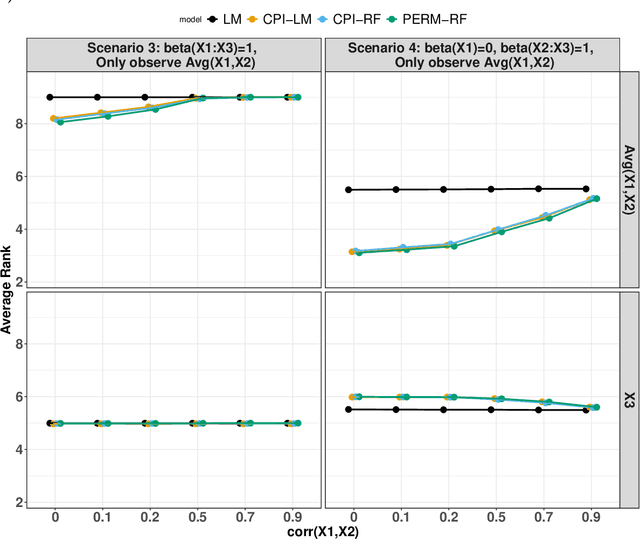
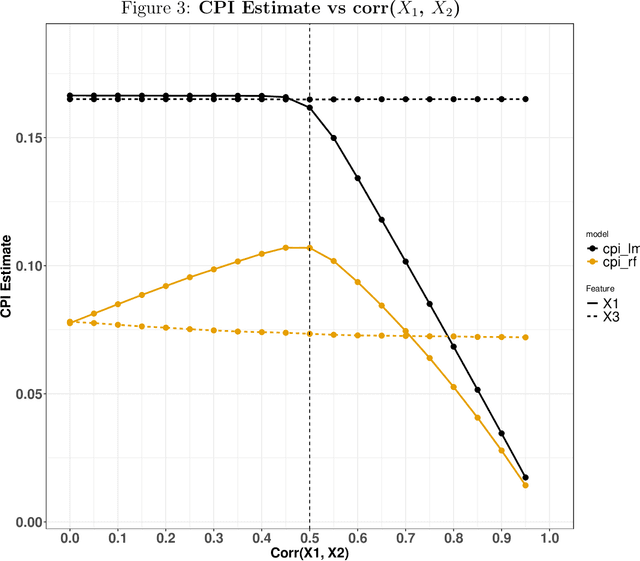
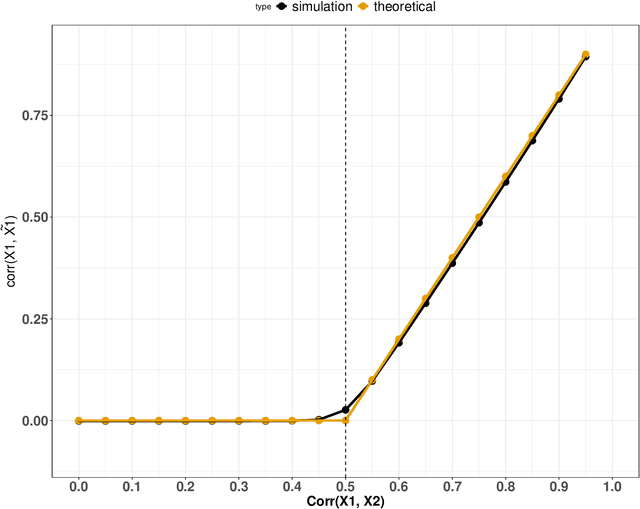
Variable importance plays a pivotal role in interpretable machine learning as it helps measure the impact of factors on the output of the prediction model. Model agnostic methods based on the generation of "null" features via permutation (or related approaches) can be applied. Such analysis is often utilized in pharmaceutical applications due to its ability to interpret black-box models, including tree-based ensembles. A major challenge and significant confounder in variable importance estimation however is the presence of between-feature correlation. Recently, several adjustments to marginal permutation utilizing feature knockoffs were proposed to address this issue, such as the variable importance measure known as conditional predictive impact (CPI). Assessment and evaluation of such approaches is the focus of our work. We first present a comprehensive simulation study investigating the impact of feature correlation on the assessment of variable importance. We then theoretically prove the limitation that highly correlated features pose for the CPI through the knockoff construction. While we expect that there is always no correlation between knockoff variables and its corresponding predictor variables, we prove that the correlation increases linearly beyond a certain correlation threshold between the predictor variables. Our findings emphasize the absence of free lunch when dealing with high feature correlation, as well as the necessity of understanding the utility and limitations behind methods in variable importance estimation.

CAPITAL: Optimal Subgroup Identification via Constrained Policy Tree Search

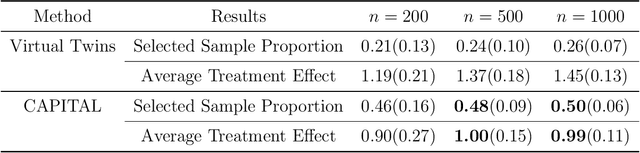
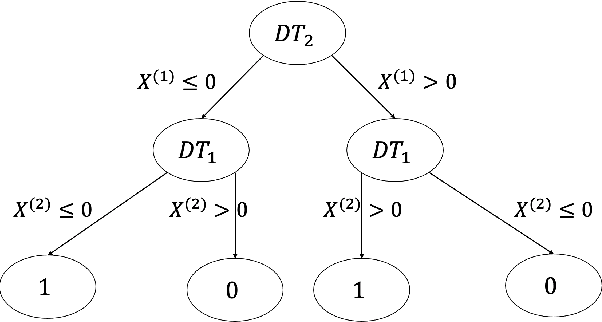
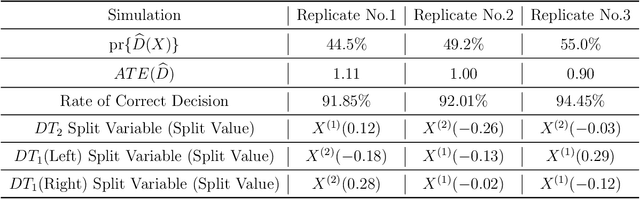
Personalized medicine, a paradigm of medicine tailored to a patient's characteristics, is an increasingly attractive field in health care. An important goal of personalized medicine is to identify a subgroup of patients, based on baseline covariates, that benefits more from the targeted treatment than other comparative treatments. Most of the current subgroup identification methods only focus on obtaining a subgroup with an enhanced treatment effect without paying attention to subgroup size. Yet, a clinically meaningful subgroup learning approach should identify the maximum number of patients who can benefit from the better treatment. In this paper, we present an optimal subgroup selection rule (SSR) that maximizes the number of selected patients, and in the meantime, achieves the pre-specified clinically meaningful mean outcome, such as the average treatment effect. We derive two equivalent theoretical forms of the optimal SSR based on the contrast function that describes the treatment-covariates interaction in the outcome. We further propose a ConstrAined PolIcy Tree seArch aLgorithm (CAPITAL) to find the optimal SSR within the interpretable decision tree class. The proposed method is flexible to handle multiple constraints that penalize the inclusion of patients with negative treatment effects, and to address time to event data using the restricted mean survival time as the clinically interesting mean outcome. Extensive simulations, comparison studies, and real data applications are conducted to demonstrate the validity and utility of our method.