Wenbin Lu
Off-Policy Evaluation Under Nonignorable Missing Data
Jul 09, 2025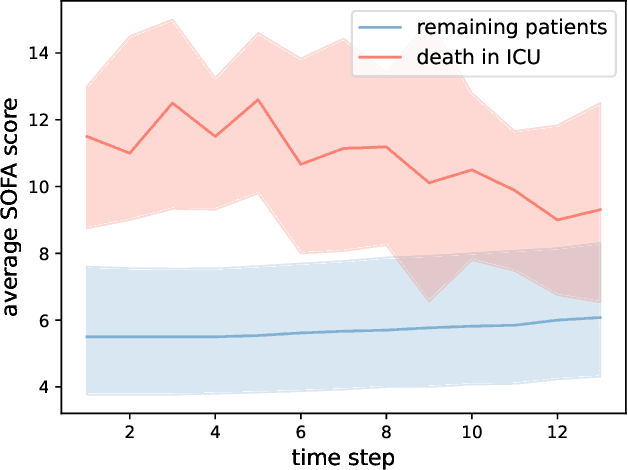
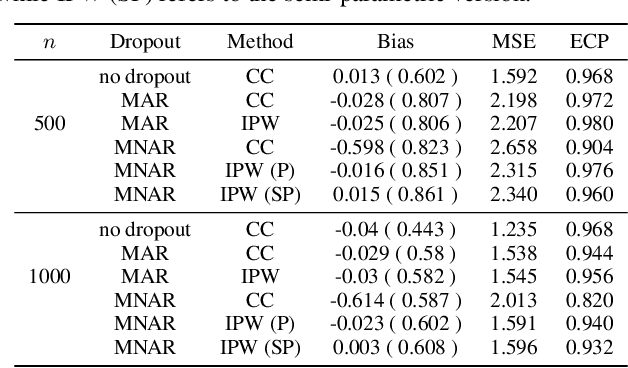
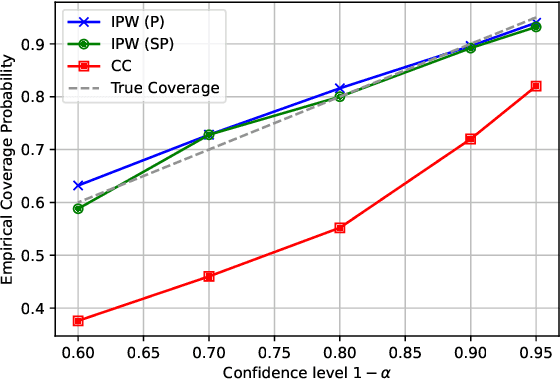
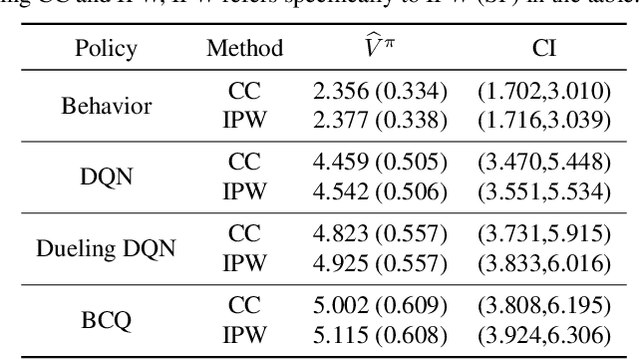
Abstract:Off-Policy Evaluation (OPE) aims to estimate the value of a target policy using offline data collected from potentially different policies. In real-world applications, however, logged data often suffers from missingness. While OPE has been extensively studied in the literature, a theoretical understanding of how missing data affects OPE results remains unclear. In this paper, we investigate OPE in the presence of monotone missingness and theoretically demonstrate that the value estimates remain unbiased under ignorable missingness but can be biased under nonignorable (informative) missingness. To retain the consistency of value estimation, we propose an inverse probability weighted value estimator and conduct statistical inference to quantify the uncertainty of the estimates. Through a series of numerical experiments, we empirically demonstrate that our proposed estimator yields a more reliable value inference under missing data.
Self-Consistent Equation-guided Neural Networks for Censored Time-to-Event Data
Mar 12, 2025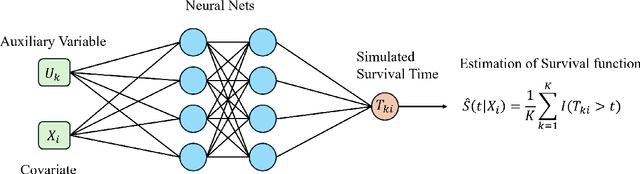

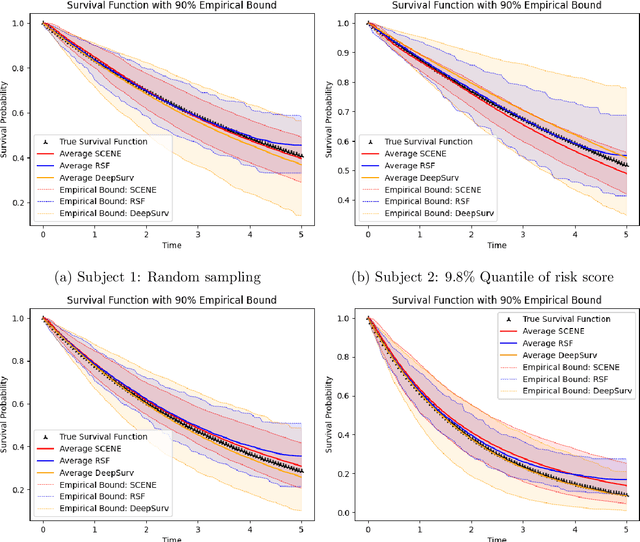
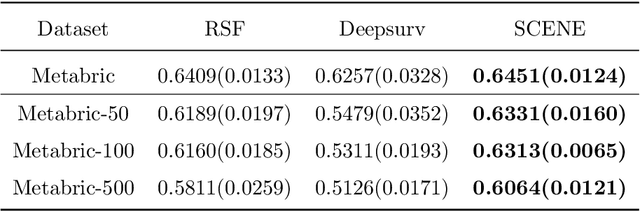
Abstract:In survival analysis, estimating the conditional survival function given predictors is often of interest. There is a growing trend in the development of deep learning methods for analyzing censored time-to-event data, especially when dealing with high-dimensional predictors that are complexly interrelated. Many existing deep learning approaches for estimating the conditional survival functions extend the Cox regression models by replacing the linear function of predictor effects by a shallow feed-forward neural network while maintaining the proportional hazards assumption. Their implementation can be computationally intensive due to the use of the full dataset at each iteration because the use of batch data may distort the at-risk set of the partial likelihood function. To overcome these limitations, we propose a novel deep learning approach to non-parametric estimation of the conditional survival functions using the generative adversarial networks leveraging self-consistent equations. The proposed method is model-free and does not require any parametric assumptions on the structure of the conditional survival function. We establish the convergence rate of our proposed estimator of the conditional survival function. In addition, we evaluate the performance of the proposed method through simulation studies and demonstrate its application on a real-world dataset.
Mining the Factor Zoo: Estimation of Latent Factor Models with Sufficient Proxies
Jan 03, 2023Abstract:Latent factor model estimation typically relies on either using domain knowledge to manually pick several observed covariates as factor proxies, or purely conducting multivariate analysis such as principal component analysis. However, the former approach may suffer from the bias while the latter can not incorporate additional information. We propose to bridge these two approaches while allowing the number of factor proxies to diverge, and hence make the latent factor model estimation robust, flexible, and statistically more accurate. As a bonus, the number of factors is also allowed to grow. At the heart of our method is a penalized reduced rank regression to combine information. To further deal with heavy-tailed data, a computationally attractive penalized robust reduced rank regression method is proposed. We establish faster rates of convergence compared with the benchmark. Extensive simulations and real examples are used to illustrate the advantages.
Adaptive Semi-Supervised Inference for Optimal Treatment Decisions with Electronic Medical Record Data
Mar 04, 2022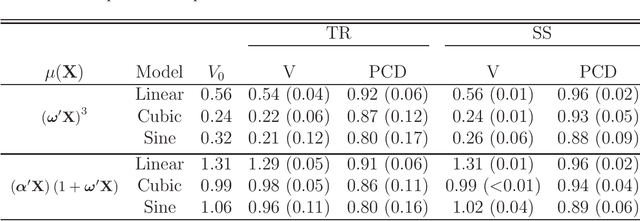

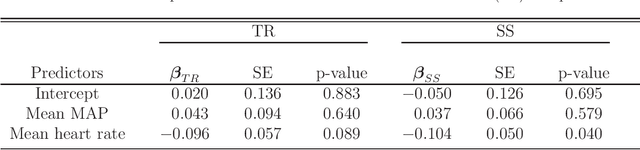

Abstract:A treatment regime is a rule that assigns a treatment to patients based on their covariate information. Recently, estimation of the optimal treatment regime that yields the greatest overall expected clinical outcome of interest has attracted a lot of attention. In this work, we consider estimation of the optimal treatment regime with electronic medical record data under a semi-supervised setting. Here, data consist of two parts: a set of `labeled' patients for whom we have the covariate, treatment and outcome information, and a much larger set of `unlabeled' patients for whom we only have the covariate information. We proposes an imputation-based semi-supervised method, utilizing `unlabeled' individuals to obtain a more efficient estimator of the optimal treatment regime. The asymptotic properties of the proposed estimators and their associated inference procedure are provided. Simulation studies are conducted to assess the empirical performance of the proposed method and to compare with a fully supervised method using only the labeled data. An application to an electronic medical record data set on the treatment of hypotensive episodes during intensive care unit (ICU) stays is also given for further illustration.
On Learning and Testing of Counterfactual Fairness through Data Preprocessing
Feb 25, 2022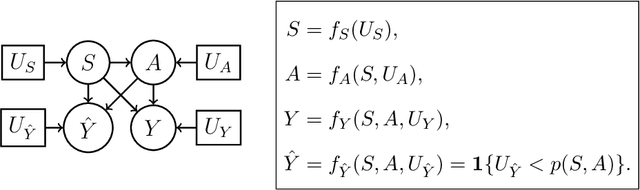
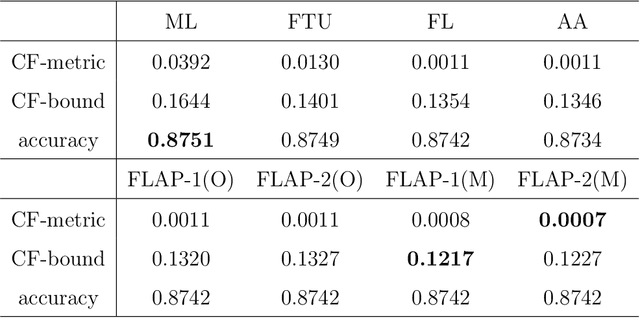
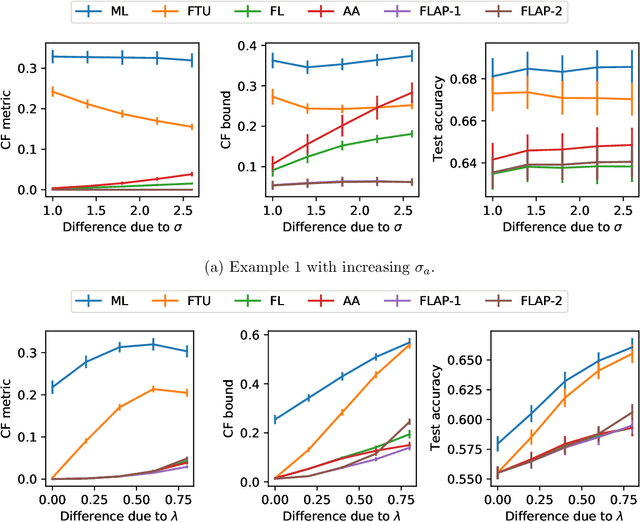
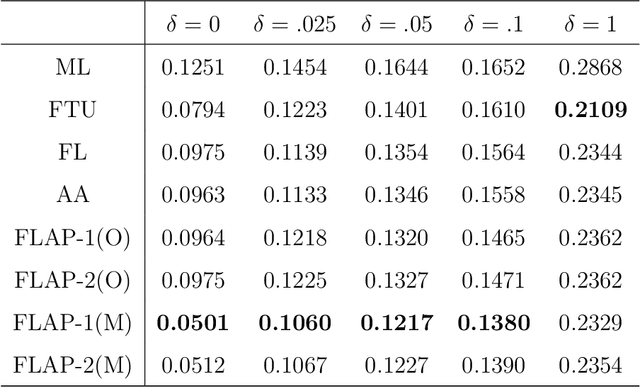
Abstract:Machine learning has become more important in real-life decision-making but people are concerned about the ethical problems it may bring when used improperly. Recent work brings the discussion of machine learning fairness into the causal framework and elaborates on the concept of Counterfactual Fairness. In this paper, we develop the Fair Learning through dAta Preprocessing (FLAP) algorithm to learn counterfactually fair decisions from biased training data and formalize the conditions where different data preprocessing procedures should be used to guarantee counterfactual fairness. We also show that Counterfactual Fairness is equivalent to the conditional independence of the decisions and the sensitive attributes given the processed non-sensitive attributes, which enables us to detect discrimination in the original decision using the processed data. The performance of our algorithm is illustrated using simulated data and real-world applications.
Targeted Optimal Treatment Regime Learning Using Summary Statistics
Jan 17, 2022
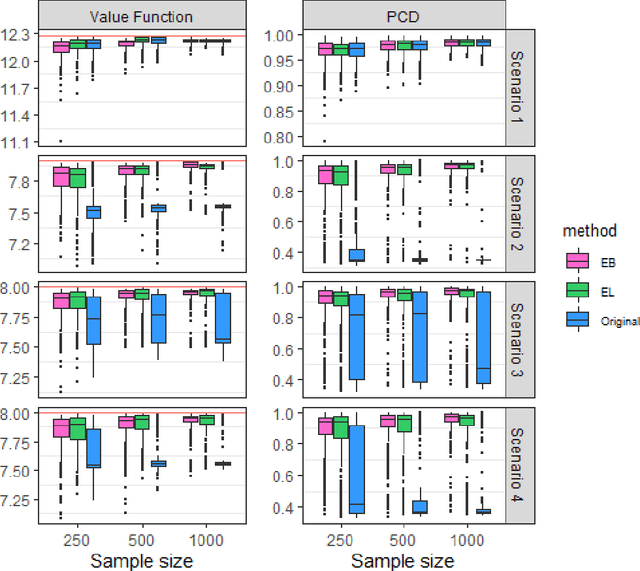
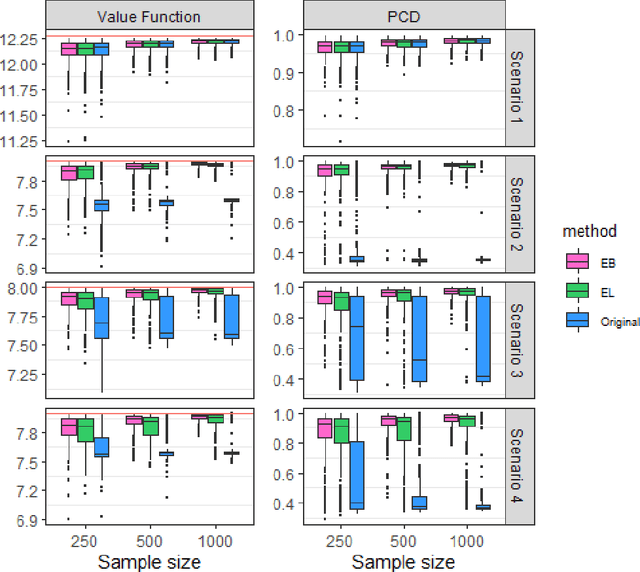

Abstract:Personalized decision-making, aiming to derive optimal individualized treatment rules (ITRs) based on individual characteristics, has recently attracted increasing attention in many fields, such as medicine, social services, and economics. Current literature mainly focuses on estimating ITRs from a single source population. In real-world applications, the distribution of a target population can be different from that of the source population. Therefore, ITRs learned by existing methods may not generalize well to the target population. Due to privacy concerns and other practical issues, individual-level data from the target population is often not available, which makes ITR learning more challenging. We consider an ITR estimation problem where the source and target populations may be heterogeneous, individual data is available from the source population, and only the summary information of covariates, such as moments, is accessible from the target population. We develop a weighting framework that tailors an ITR for a given target population by leveraging the available summary statistics. Specifically, we propose a calibrated augmented inverse probability weighted estimator of the value function for the target population and estimate an optimal ITR by maximizing this estimator within a class of pre-specified ITRs. We show that the proposed calibrated estimator is consistent and asymptotically normal even with flexible semi/nonparametric models for nuisance function approximation, and the variance of the value estimator can be consistently estimated. We demonstrate the empirical performance of the proposed method using simulation studies and a real application to an eICU dataset as the source sample and a MIMIC-III dataset as the target sample.
Jump Interval-Learning for Individualized Decision Making
Nov 17, 2021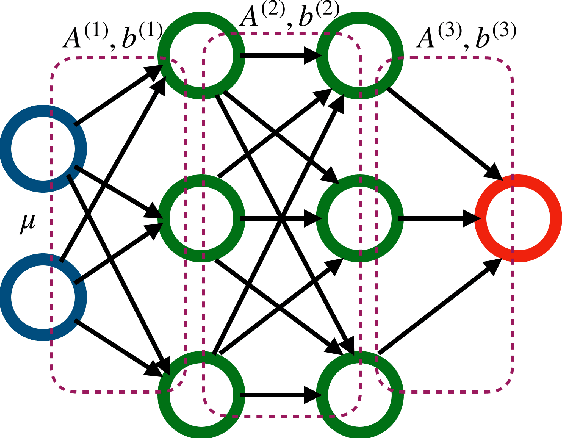
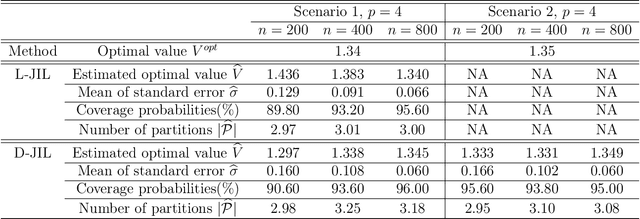
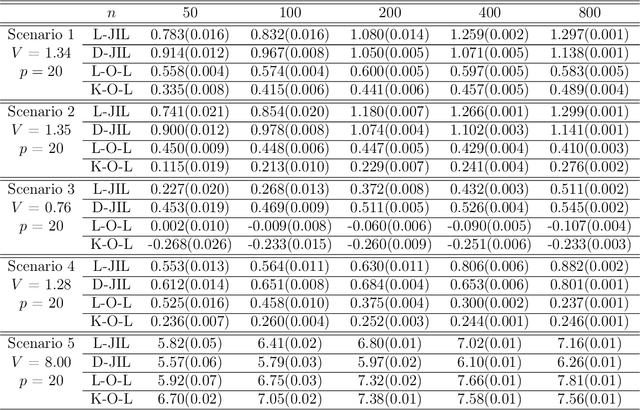
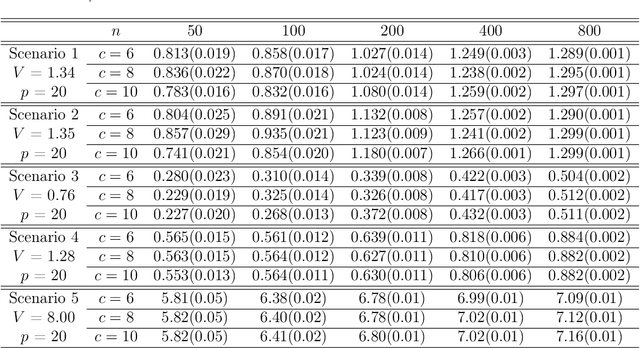
Abstract:An individualized decision rule (IDR) is a decision function that assigns each individual a given treatment based on his/her observed characteristics. Most of the existing works in the literature consider settings with binary or finitely many treatment options. In this paper, we focus on the continuous treatment setting and propose a jump interval-learning to develop an individualized interval-valued decision rule (I2DR) that maximizes the expected outcome. Unlike IDRs that recommend a single treatment, the proposed I2DR yields an interval of treatment options for each individual, making it more flexible to implement in practice. To derive an optimal I2DR, our jump interval-learning method estimates the conditional mean of the outcome given the treatment and the covariates via jump penalized regression, and derives the corresponding optimal I2DR based on the estimated outcome regression function. The regressor is allowed to be either linear for clear interpretation or deep neural network to model complex treatment-covariates interactions. To implement jump interval-learning, we develop a searching algorithm based on dynamic programming that efficiently computes the outcome regression function. Statistical properties of the resulting I2DR are established when the outcome regression function is either a piecewise or continuous function over the treatment space. We further develop a procedure to infer the mean outcome under the (estimated) optimal policy. Extensive simulations and a real data application to a warfarin study are conducted to demonstrate the empirical validity of the proposed I2DR.
A Probit Tensor Factorization Model For Relational Learning
Nov 09, 2021
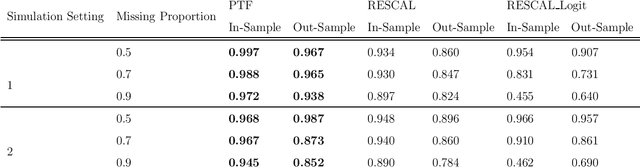
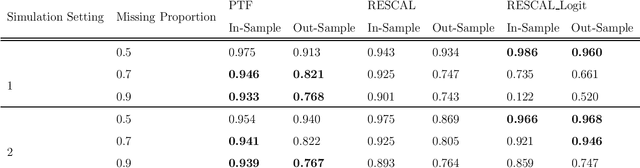

Abstract:With the proliferation of knowledge graphs, modeling data with complex multirelational structure has gained increasing attention in the area of statistical relational learning. One of the most important goals of statistical relational learning is link prediction, i.e., predicting whether certain relations exist in the knowledge graph. A large number of models and algorithms have been proposed to perform link prediction, among which tensor factorization method has proven to achieve state-of-the-art performance in terms of computation efficiency and prediction accuracy. However, a common drawback of the existing tensor factorization models is that the missing relations and non-existing relations are treated in the same way, which results in a loss of information. To address this issue, we propose a binary tensor factorization model with probit link, which not only inherits the computation efficiency from the classic tensor factorization model but also accounts for the binary nature of relational data. Our proposed probit tensor factorization (PTF) model shows advantages in both the prediction accuracy and interpretability
CAPITAL: Optimal Subgroup Identification via Constrained Policy Tree Search
Oct 11, 2021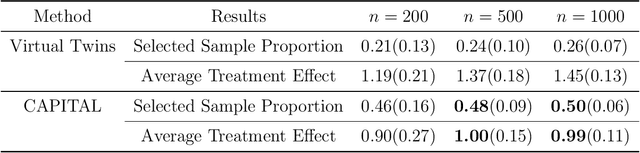
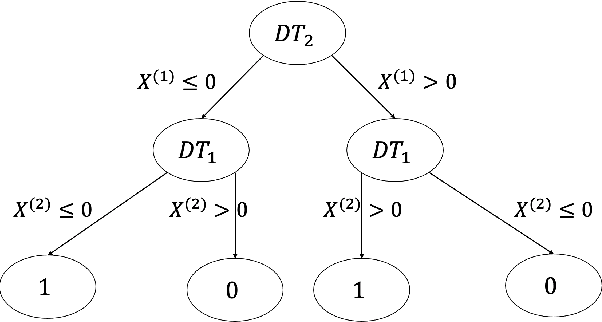
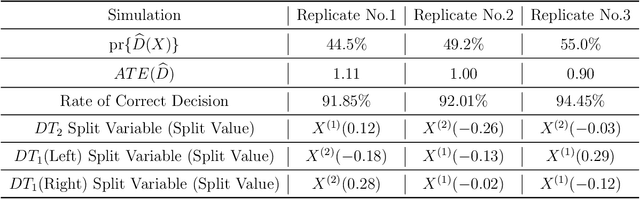
Abstract:Personalized medicine, a paradigm of medicine tailored to a patient's characteristics, is an increasingly attractive field in health care. An important goal of personalized medicine is to identify a subgroup of patients, based on baseline covariates, that benefits more from the targeted treatment than other comparative treatments. Most of the current subgroup identification methods only focus on obtaining a subgroup with an enhanced treatment effect without paying attention to subgroup size. Yet, a clinically meaningful subgroup learning approach should identify the maximum number of patients who can benefit from the better treatment. In this paper, we present an optimal subgroup selection rule (SSR) that maximizes the number of selected patients, and in the meantime, achieves the pre-specified clinically meaningful mean outcome, such as the average treatment effect. We derive two equivalent theoretical forms of the optimal SSR based on the contrast function that describes the treatment-covariates interaction in the outcome. We further propose a ConstrAined PolIcy Tree seArch aLgorithm (CAPITAL) to find the optimal SSR within the interpretable decision tree class. The proposed method is flexible to handle multiple constraints that penalize the inclusion of patients with negative treatment effects, and to address time to event data using the restricted mean survival time as the clinically interesting mean outcome. Extensive simulations, comparison studies, and real data applications are conducted to demonstrate the validity and utility of our method.
GEAR: On Optimal Decision Making with Auxiliary Data
Apr 21, 2021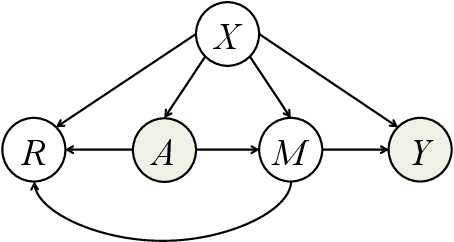
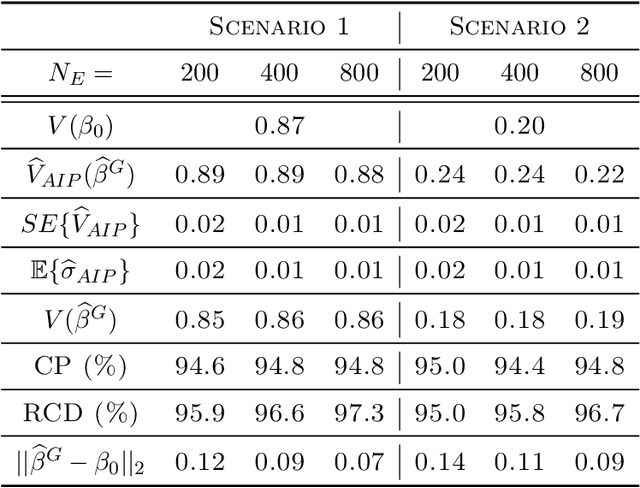
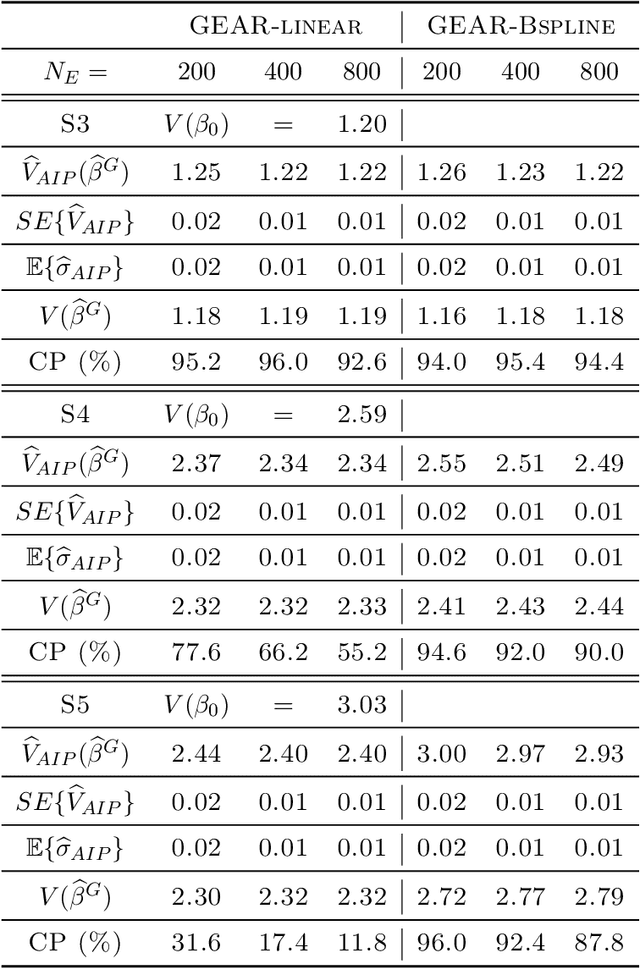
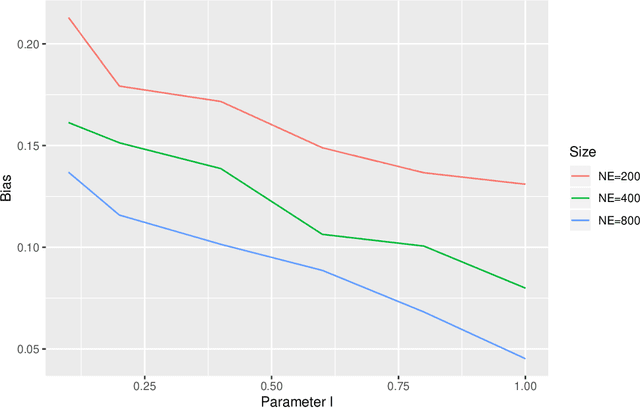
Abstract:Personalized optimal decision making, finding the optimal decision rule (ODR) based on individual characteristics, has attracted increasing attention recently in many fields, such as education, economics, and medicine. Current ODR methods usually require the primary outcome of interest in samples for assessing treatment effects, namely the experimental sample. However, in many studies, treatments may have a long-term effect, and as such the primary outcome of interest cannot be observed in the experimental sample due to the limited duration of experiments, which makes the estimation of ODR impossible. This paper is inspired to address this challenge by making use of an auxiliary sample to facilitate the estimation of ODR in the experimental sample. We propose an auGmented inverse propensity weighted Experimental and Auxiliary sample-based decision Rule (GEAR) by maximizing the augmented inverse propensity weighted value estimator over a class of decision rules using the experimental sample, with the primary outcome being imputed based on the auxiliary sample. The asymptotic properties of the proposed GEAR estimators and their associated value estimators are established. Simulation studies are conducted to demonstrate its empirical validity with a real AIDS application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge