Extended Fiducial Inference for Individual Treatment Effects via Deep Neural Networks

Individual treatment effect estimation has gained significant attention in recent data science literature. This work introduces the Double Neural Network (Double-NN) method to address this problem within the framework of extended fiducial inference (EFI). In the proposed method, deep neural networks are used to model the treatment and control effect functions, while an additional neural network is employed to estimate their parameters. The universal approximation capability of deep neural networks ensures the broad applicability of this method. Numerical results highlight the superior performance of the proposed Double-NN method compared to the conformal quantile regression (CQR) method in individual treatment effect estimation. From the perspective of statistical inference, this work advances the theory and methodology for statistical inference of large models. Specifically, it is theoretically proven that the proposed method permits the model size to increase with the sample size $n$ at a rate of $O(n^{\zeta})$ for some $0 \leq \zeta<1$, while still maintaining proper quantification of uncertainty in the model parameters. This result marks a significant improvement compared to the range $0\leq \zeta < \frac{1}{2}$ required by the classical central limit theorem. Furthermore, this work provides a rigorous framework for quantifying the uncertainty of deep neural networks under the neural scaling law, representing a substantial contribution to the statistical understanding of large-scale neural network models.

Self-Consistent Equation-guided Neural Networks for Censored Time-to-Event Data

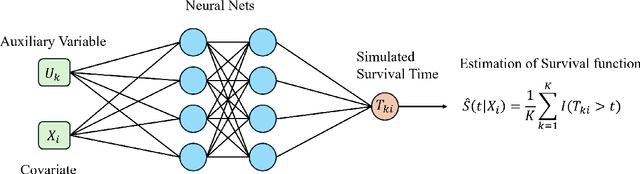
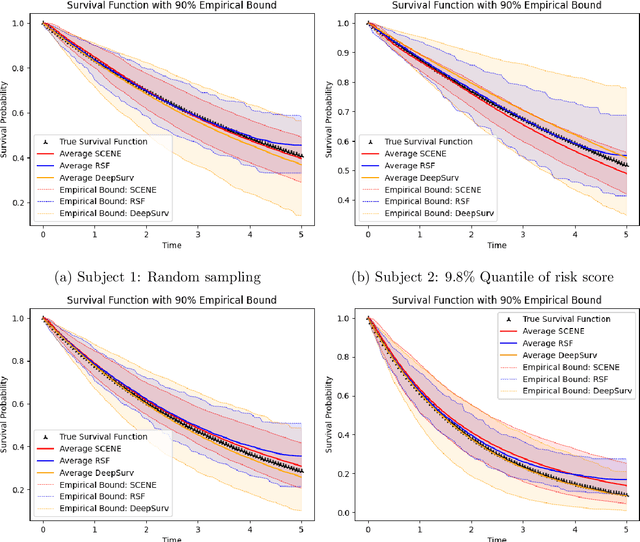
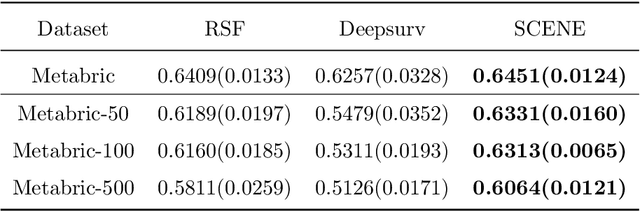
In survival analysis, estimating the conditional survival function given predictors is often of interest. There is a growing trend in the development of deep learning methods for analyzing censored time-to-event data, especially when dealing with high-dimensional predictors that are complexly interrelated. Many existing deep learning approaches for estimating the conditional survival functions extend the Cox regression models by replacing the linear function of predictor effects by a shallow feed-forward neural network while maintaining the proportional hazards assumption. Their implementation can be computationally intensive due to the use of the full dataset at each iteration because the use of batch data may distort the at-risk set of the partial likelihood function. To overcome these limitations, we propose a novel deep learning approach to non-parametric estimation of the conditional survival functions using the generative adversarial networks leveraging self-consistent equations. The proposed method is model-free and does not require any parametric assumptions on the structure of the conditional survival function. We establish the convergence rate of our proposed estimator of the conditional survival function. In addition, we evaluate the performance of the proposed method through simulation studies and demonstrate its application on a real-world dataset.

Constructing Fair Latent Space for Intersection of Fairness and Explainability

As the use of machine learning models has increased, numerous studies have aimed to enhance fairness. However, research on the intersection of fairness and explainability remains insufficient, leading to potential issues in gaining the trust of actual users. Here, we propose a novel module that constructs a fair latent space, enabling faithful explanation while ensuring fairness. The fair latent space is constructed by disentangling and redistributing labels and sensitive attributes, allowing the generation of counterfactual explanations for each type of information. Our module is attached to a pretrained generative model, transforming its biased latent space into a fair latent space. Additionally, since only the module needs to be trained, there are advantages in terms of time and cost savings, without the need to train the entire generative model. We validate the fair latent space with various fairness metrics and demonstrate that our approach can effectively provide explanations for biased decisions and assurances of fairness.

Mitigating Spurious Correlations via Disagreement Probability

Models trained with empirical risk minimization (ERM) are prone to be biased towards spurious correlations between target labels and bias attributes, which leads to poor performance on data groups lacking spurious correlations. It is particularly challenging to address this problem when access to bias labels is not permitted. To mitigate the effect of spurious correlations without bias labels, we first introduce a novel training objective designed to robustly enhance model performance across all data samples, irrespective of the presence of spurious correlations. From this objective, we then derive a debiasing method, Disagreement Probability based Resampling for debiasing (DPR), which does not require bias labels. DPR leverages the disagreement between the target label and the prediction of a biased model to identify bias-conflicting samples-those without spurious correlations-and upsamples them according to the disagreement probability. Empirical evaluations on multiple benchmarks demonstrate that DPR achieves state-of-the-art performance over existing baselines that do not use bias labels. Furthermore, we provide a theoretical analysis that details how DPR reduces dependency on spurious correlations.

Extended Fiducial Inference: Toward an Automated Process of Statistical Inference

While fiducial inference was widely considered a big blunder by R.A. Fisher, the goal he initially set --`inferring the uncertainty of model parameters on the basis of observations' -- has been continually pursued by many statisticians. To this end, we develop a new statistical inference method called extended Fiducial inference (EFI). The new method achieves the goal of fiducial inference by leveraging advanced statistical computing techniques while remaining scalable for big data. EFI involves jointly imputing random errors realized in observations using stochastic gradient Markov chain Monte Carlo and estimating the inverse function using a sparse deep neural network (DNN). The consistency of the sparse DNN estimator ensures that the uncertainty embedded in observations is properly propagated to model parameters through the estimated inverse function, thereby validating downstream statistical inference. Compared to frequentist and Bayesian methods, EFI offers significant advantages in parameter estimation and hypothesis testing. Specifically, EFI provides higher fidelity in parameter estimation, especially when outliers are present in the observations; and eliminates the need for theoretical reference distributions in hypothesis testing, thereby automating the statistical inference process. EFI also provides an innovative framework for semi-supervised learning.

A New Paradigm for Generative Adversarial Networks based on Randomized Decision Rules

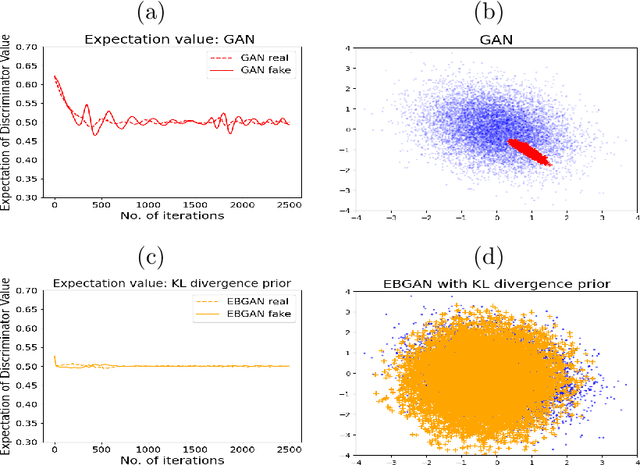
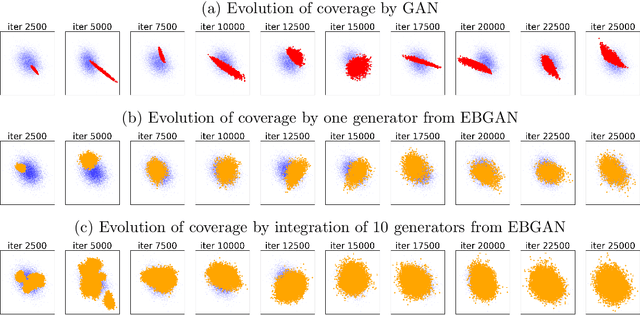
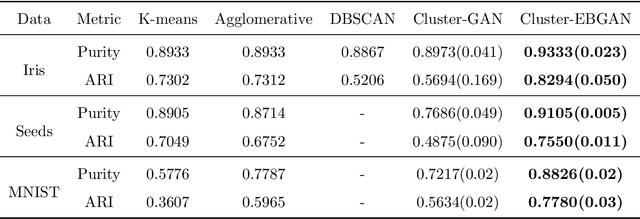
The Generative Adversarial Network (GAN) was recently introduced in the literature as a novel machine learning method for training generative models. It has many applications in statistics such as nonparametric clustering and nonparametric conditional independence tests. However, training the GAN is notoriously difficult due to the issue of mode collapse, which refers to the lack of diversity among generated data. In this paper, we identify the reasons why the GAN suffers from this issue, and to address it, we propose a new formulation for the GAN based on randomized decision rules. In the new formulation, the discriminator converges to a fixed point while the generator converges to a distribution at the Nash equilibrium. We propose to train the GAN by an empirical Bayes-like method by treating the discriminator as a hyper-parameter of the posterior distribution of the generator. Specifically, we simulate generators from its posterior distribution conditioned on the discriminator using a stochastic gradient Markov chain Monte Carlo (MCMC) algorithm, and update the discriminator using stochastic gradient descent along with simulations of the generators. We establish convergence of the proposed method to the Nash equilibrium. Apart from image generation, we apply the proposed method to nonparametric clustering and nonparametric conditional independence tests. A portion of the numerical results is presented in the supplementary material.

Differentially Private Topological Data Analysis

This paper is the first to attempt differentially private (DP) topological data analysis (TDA), producing near-optimal private persistence diagrams. We analyze the sensitivity of persistence diagrams in terms of the bottleneck distance, and we show that the commonly used \v{C}ech complex has sensitivity that does not decrease as the sample size $n$ increases. This makes it challenging for the persistence diagrams of \v{C}ech complexes to be privatized. As an alternative, we show that the persistence diagram obtained by the $L^1$-distance to measure (DTM) has sensitivity $O(1/n)$. Based on the sensitivity analysis, we propose using the exponential mechanism whose utility function is defined in terms of the bottleneck distance of the $L^1$-DTM persistence diagrams. We also derive upper and lower bounds of the accuracy of our privacy mechanism; the obtained bounds indicate that the privacy error of our mechanism is near-optimal. We demonstrate the performance of our privatized persistence diagrams through simulations as well as on a real dataset tracking human movement.

Melon Playlist Dataset: a public dataset for audio-based playlist generation and music tagging

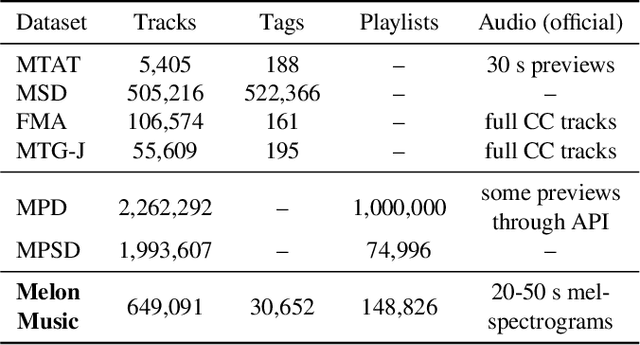
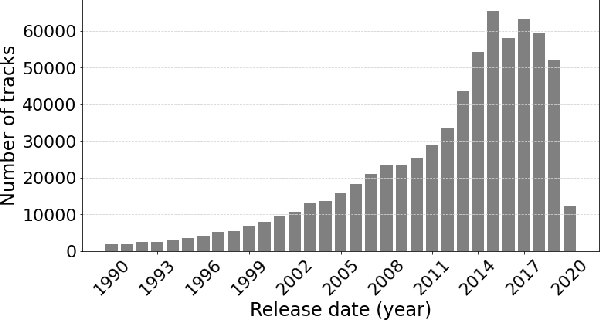
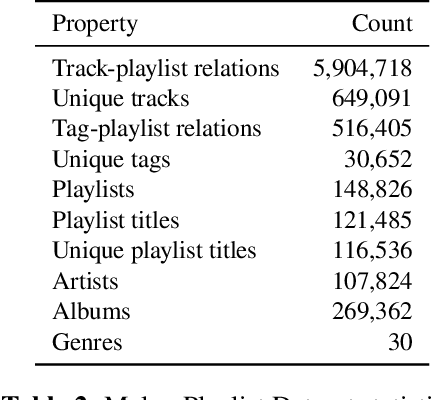
One of the main limitations in the field of audio signal processing is the lack of large public datasets with audio representations and high-quality annotations due to restrictions of copyrighted commercial music. We present Melon Playlist Dataset, a public dataset of mel-spectrograms for 649,091tracks and 148,826 associated playlists annotated by 30,652 different tags. All the data is gathered from Melon, a popular Korean streaming service. The dataset is suitable for music information retrieval tasks, in particular, auto-tagging and automatic playlist continuation. Even though the latter can be addressed by collaborative filtering approaches, audio provides opportunities for research on track suggestions and building systems resistant to the cold-start problem, for which we provide a baseline. Moreover, the playlists and the annotations included in the Melon Playlist Dataset make it suitable for metric learning and representation learning.

Stochastic Gradient Langevin Dynamics Algorithms with Adaptive Drifts

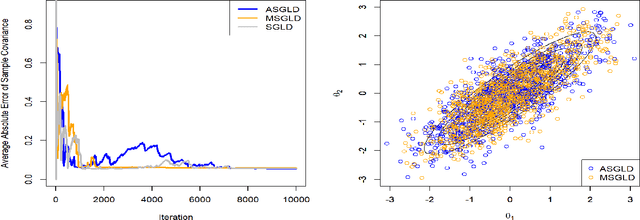
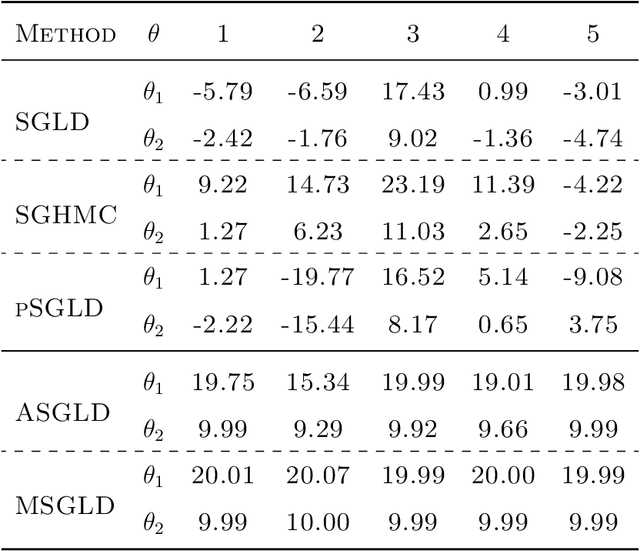
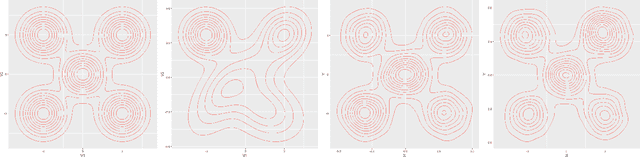
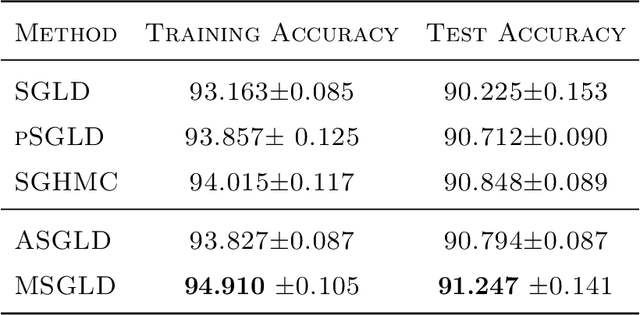
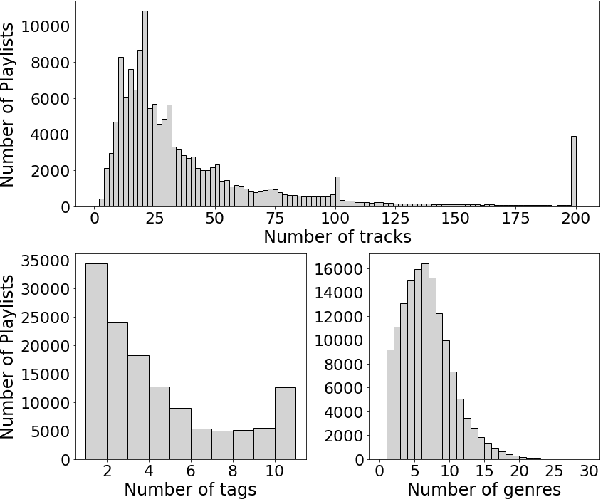
Bayesian deep learning offers a principled way to address many issues concerning safety of artificial intelligence (AI), such as model uncertainty,model interpretability, and prediction bias. However, due to the lack of efficient Monte Carlo algorithms for sampling from the posterior of deep neural networks (DNNs), Bayesian deep learning has not yet powered our AI system. We propose a class of adaptive stochastic gradient Markov chain Monte Carlo (SGMCMC) algorithms, where the drift function is biased to enhance escape from saddle points and the bias is adaptively adjusted according to the gradient of past samples. We establish the convergence of the proposed algorithms under mild conditions, and demonstrate via numerical examples that the proposed algorithms can significantly outperform the existing SGMCMC algorithms, such as stochastic gradient Langevin dynamics (SGLD), stochastic gradient Hamiltonian Monte Carlo (SGHMC) and preconditioned SGLD, in both simulation and optimization tasks.