A New Paradigm for Generative Adversarial Networks based on Randomized Decision Rules
Paper and Code
Jun 23, 2023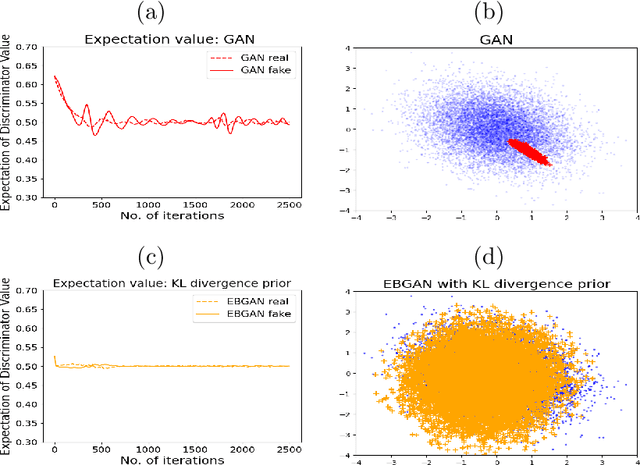

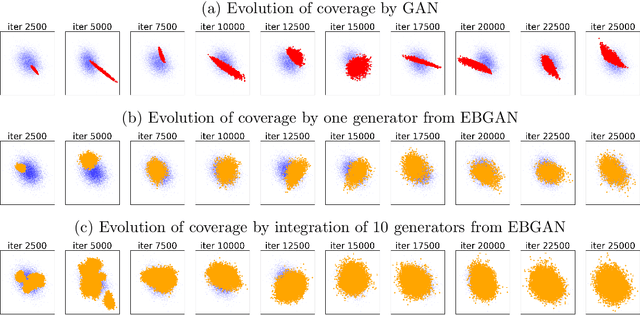
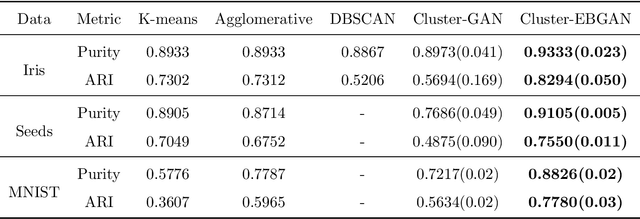
The Generative Adversarial Network (GAN) was recently introduced in the literature as a novel machine learning method for training generative models. It has many applications in statistics such as nonparametric clustering and nonparametric conditional independence tests. However, training the GAN is notoriously difficult due to the issue of mode collapse, which refers to the lack of diversity among generated data. In this paper, we identify the reasons why the GAN suffers from this issue, and to address it, we propose a new formulation for the GAN based on randomized decision rules. In the new formulation, the discriminator converges to a fixed point while the generator converges to a distribution at the Nash equilibrium. We propose to train the GAN by an empirical Bayes-like method by treating the discriminator as a hyper-parameter of the posterior distribution of the generator. Specifically, we simulate generators from its posterior distribution conditioned on the discriminator using a stochastic gradient Markov chain Monte Carlo (MCMC) algorithm, and update the discriminator using stochastic gradient descent along with simulations of the generators. We establish convergence of the proposed method to the Nash equilibrium. Apart from image generation, we apply the proposed method to nonparametric clustering and nonparametric conditional independence tests. A portion of the numerical results is presented in the supplementary material.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge