Uncertainty Quantification for Physics-Informed Neural Networks with Extended Fiducial Inference

Uncertainty quantification (UQ) in scientific machine learning is increasingly critical as neural networks are widely adopted to tackle complex problems across diverse scientific disciplines. For physics-informed neural networks (PINNs), a prominent model in scientific machine learning, uncertainty is typically quantified using Bayesian or dropout methods. However, both approaches suffer from a fundamental limitation: the prior distribution or dropout rate required to construct honest confidence sets cannot be determined without additional information. In this paper, we propose a novel method within the framework of extended fiducial inference (EFI) to provide rigorous uncertainty quantification for PINNs. The proposed method leverages a narrow-neck hyper-network to learn the parameters of the PINN and quantify their uncertainty based on imputed random errors in the observations. This approach overcomes the limitations of Bayesian and dropout methods, enabling the construction of honest confidence sets based solely on observed data. This advancement represents a significant breakthrough for PINNs, greatly enhancing their reliability, interpretability, and applicability to real-world scientific and engineering challenges. Moreover, it establishes a new theoretical framework for EFI, extending its application to large-scale models, eliminating the need for sparse hyper-networks, and significantly improving the automaticity and robustness of statistical inference.

Extended Fiducial Inference for Individual Treatment Effects via Deep Neural Networks

Individual treatment effect estimation has gained significant attention in recent data science literature. This work introduces the Double Neural Network (Double-NN) method to address this problem within the framework of extended fiducial inference (EFI). In the proposed method, deep neural networks are used to model the treatment and control effect functions, while an additional neural network is employed to estimate their parameters. The universal approximation capability of deep neural networks ensures the broad applicability of this method. Numerical results highlight the superior performance of the proposed Double-NN method compared to the conformal quantile regression (CQR) method in individual treatment effect estimation. From the perspective of statistical inference, this work advances the theory and methodology for statistical inference of large models. Specifically, it is theoretically proven that the proposed method permits the model size to increase with the sample size $n$ at a rate of $O(n^{\zeta})$ for some $0 \leq \zeta<1$, while still maintaining proper quantification of uncertainty in the model parameters. This result marks a significant improvement compared to the range $0\leq \zeta < \frac{1}{2}$ required by the classical central limit theorem. Furthermore, this work provides a rigorous framework for quantifying the uncertainty of deep neural networks under the neural scaling law, representing a substantial contribution to the statistical understanding of large-scale neural network models.

Magnitude Pruning of Large Pretrained Transformer Models with a Mixture Gaussian Prior

Large pretrained transformer models have revolutionized modern AI applications with their state-of-the-art performance in natural language processing (NLP). However, their substantial parameter count poses challenges for real-world deployment. To address this, researchers often reduce model size by pruning parameters based on their magnitude or sensitivity. Previous research has demonstrated the limitations of magnitude pruning, especially in the context of transfer learning for modern NLP tasks. In this paper, we introduce a new magnitude-based pruning algorithm called mixture Gaussian prior pruning (MGPP), which employs a mixture Gaussian prior for regularization. MGPP prunes non-expressive weights under the guidance of the mixture Gaussian prior, aiming to retain the model's expressive capability. Extensive evaluations across various NLP tasks, including natural language understanding, question answering, and natural language generation, demonstrate the superiority of MGPP over existing pruning methods, particularly in high sparsity settings. Additionally, we provide a theoretical justification for the consistency of the sparse transformer, shedding light on the effectiveness of the proposed pruning method.

Extended Fiducial Inference: Toward an Automated Process of Statistical Inference

While fiducial inference was widely considered a big blunder by R.A. Fisher, the goal he initially set --`inferring the uncertainty of model parameters on the basis of observations' -- has been continually pursued by many statisticians. To this end, we develop a new statistical inference method called extended Fiducial inference (EFI). The new method achieves the goal of fiducial inference by leveraging advanced statistical computing techniques while remaining scalable for big data. EFI involves jointly imputing random errors realized in observations using stochastic gradient Markov chain Monte Carlo and estimating the inverse function using a sparse deep neural network (DNN). The consistency of the sparse DNN estimator ensures that the uncertainty embedded in observations is properly propagated to model parameters through the estimated inverse function, thereby validating downstream statistical inference. Compared to frequentist and Bayesian methods, EFI offers significant advantages in parameter estimation and hypothesis testing. Specifically, EFI provides higher fidelity in parameter estimation, especially when outliers are present in the observations; and eliminates the need for theoretical reference distributions in hypothesis testing, thereby automating the statistical inference process. EFI also provides an innovative framework for semi-supervised learning.

Causal-StoNet: Causal Inference for High-Dimensional Complex Data

With the advancement of data science, the collection of increasingly complex datasets has become commonplace. In such datasets, the data dimension can be extremely high, and the underlying data generation process can be unknown and highly nonlinear. As a result, the task of making causal inference with high-dimensional complex data has become a fundamental problem in many disciplines, such as medicine, econometrics, and social science. However, the existing methods for causal inference are frequently developed under the assumption that the data dimension is low or that the underlying data generation process is linear or approximately linear. To address these challenges, this paper proposes a novel causal inference approach for dealing with high-dimensional complex data. The proposed approach is based on deep learning techniques, including sparse deep learning theory and stochastic neural networks, that have been developed in recent literature. By using these techniques, the proposed approach can address both the high dimensionality and unknown data generation process in a coherent way. Furthermore, the proposed approach can also be used when missing values are present in the datasets. Extensive numerical studies indicate that the proposed approach outperforms existing ones.

Fast Value Tracking for Deep Reinforcement Learning

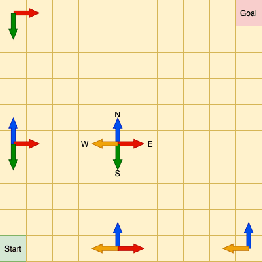
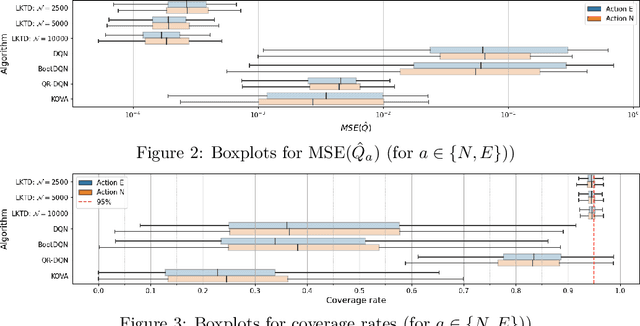
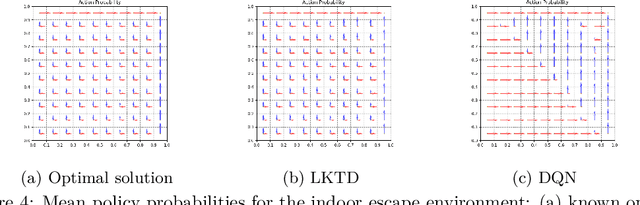
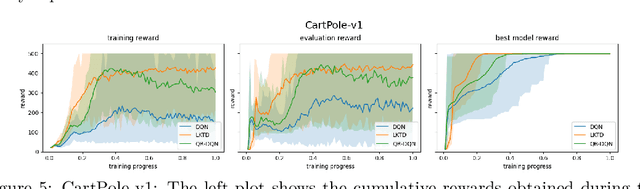
Reinforcement learning (RL) tackles sequential decision-making problems by creating agents that interacts with their environment. However, existing algorithms often view these problem as static, focusing on point estimates for model parameters to maximize expected rewards, neglecting the stochastic dynamics of agent-environment interactions and the critical role of uncertainty quantification. Our research leverages the Kalman filtering paradigm to introduce a novel and scalable sampling algorithm called Langevinized Kalman Temporal-Difference (LKTD) for deep reinforcement learning. This algorithm, grounded in Stochastic Gradient Markov Chain Monte Carlo (SGMCMC), efficiently draws samples from the posterior distribution of deep neural network parameters. Under mild conditions, we prove that the posterior samples generated by the LKTD algorithm converge to a stationary distribution. This convergence not only enables us to quantify uncertainties associated with the value function and model parameters but also allows us to monitor these uncertainties during policy updates throughout the training phase. The LKTD algorithm paves the way for more robust and adaptable reinforcement learning approaches.

Sparse Deep Learning for Time Series Data: Theory and Applications

Sparse deep learning has become a popular technique for improving the performance of deep neural networks in areas such as uncertainty quantification, variable selection, and large-scale network compression. However, most existing research has focused on problems where the observations are independent and identically distributed (i.i.d.), and there has been little work on the problems where the observations are dependent, such as time series data and sequential data in natural language processing. This paper aims to address this gap by studying the theory for sparse deep learning with dependent data. We show that sparse recurrent neural networks (RNNs) can be consistently estimated, and their predictions are asymptotically normally distributed under appropriate assumptions, enabling the prediction uncertainty to be correctly quantified. Our numerical results show that sparse deep learning outperforms state-of-the-art methods, such as conformal predictions, in prediction uncertainty quantification for time series data. Furthermore, our results indicate that the proposed method can consistently identify the autoregressive order for time series data and outperform existing methods in large-scale model compression. Our proposed method has important practical implications in fields such as finance, healthcare, and energy, where both accurate point estimates and prediction uncertainty quantification are of concern.

A New Paradigm for Generative Adversarial Networks based on Randomized Decision Rules

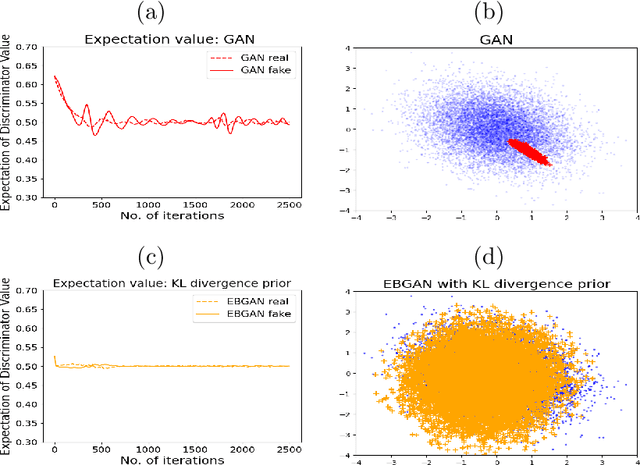
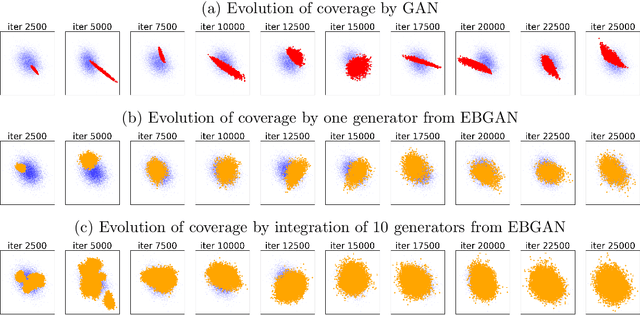
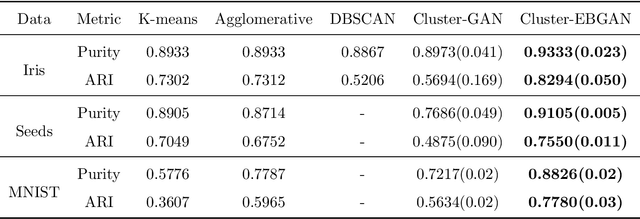
The Generative Adversarial Network (GAN) was recently introduced in the literature as a novel machine learning method for training generative models. It has many applications in statistics such as nonparametric clustering and nonparametric conditional independence tests. However, training the GAN is notoriously difficult due to the issue of mode collapse, which refers to the lack of diversity among generated data. In this paper, we identify the reasons why the GAN suffers from this issue, and to address it, we propose a new formulation for the GAN based on randomized decision rules. In the new formulation, the discriminator converges to a fixed point while the generator converges to a distribution at the Nash equilibrium. We propose to train the GAN by an empirical Bayes-like method by treating the discriminator as a hyper-parameter of the posterior distribution of the generator. Specifically, we simulate generators from its posterior distribution conditioned on the discriminator using a stochastic gradient Markov chain Monte Carlo (MCMC) algorithm, and update the discriminator using stochastic gradient descent along with simulations of the generators. We establish convergence of the proposed method to the Nash equilibrium. Apart from image generation, we apply the proposed method to nonparametric clustering and nonparametric conditional independence tests. A portion of the numerical results is presented in the supplementary material.

Non-reversible Parallel Tempering for Deep Posterior Approximation

Parallel tempering (PT), also known as replica exchange, is the go-to workhorse for simulations of multi-modal distributions. The key to the success of PT is to adopt efficient swap schemes. The popular deterministic even-odd (DEO) scheme exploits the non-reversibility property and has successfully reduced the communication cost from $O(P^2)$ to $O(P)$ given sufficiently many $P$ chains. However, such an innovation largely disappears in big data due to the limited chains and few bias-corrected swaps. To handle this issue, we generalize the DEO scheme to promote non-reversibility and propose a few solutions to tackle the underlying bias caused by the geometric stopping time. Notably, in big data scenarios, we obtain an appealing communication cost $O(P\log P)$ based on the optimal window size. In addition, we also adopt stochastic gradient descent (SGD) with large and constant learning rates as exploration kernels. Such a user-friendly nature enables us to conduct approximation tasks for complex posteriors without much tuning costs.

Nonlinear Sufficient Dimension Reduction with a Stochastic Neural Network

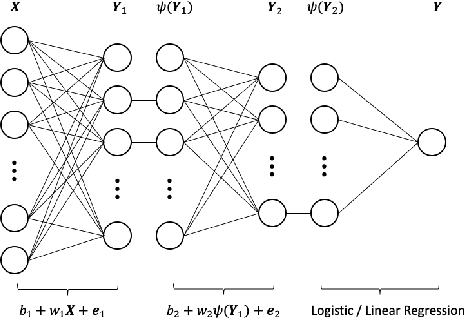
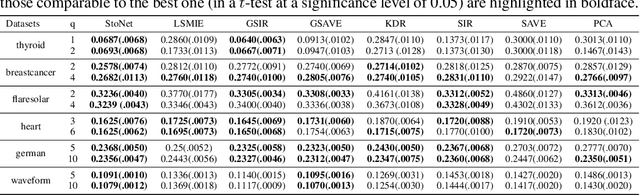
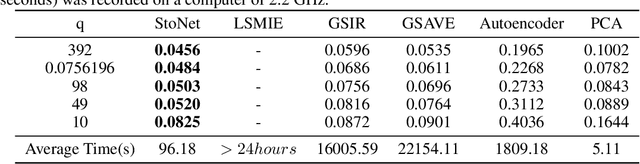
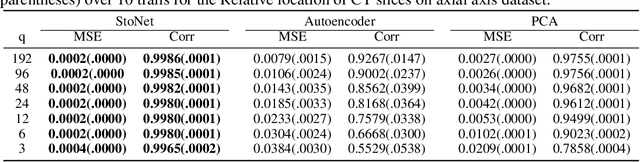
Sufficient dimension reduction is a powerful tool to extract core information hidden in the high-dimensional data and has potentially many important applications in machine learning tasks. However, the existing nonlinear sufficient dimension reduction methods often lack the scalability necessary for dealing with large-scale data. We propose a new type of stochastic neural network under a rigorous probabilistic framework and show that it can be used for sufficient dimension reduction for large-scale data. The proposed stochastic neural network is trained using an adaptive stochastic gradient Markov chain Monte Carlo algorithm, whose convergence is rigorously studied in the paper as well. Through extensive experiments on real-world classification and regression problems, we show that the proposed method compares favorably with the existing state-of-the-art sufficient dimension reduction methods and is computationally more efficient for large-scale data.