Uncertainty Quantification for Physics-Informed Neural Networks with Extended Fiducial Inference

Uncertainty quantification (UQ) in scientific machine learning is increasingly critical as neural networks are widely adopted to tackle complex problems across diverse scientific disciplines. For physics-informed neural networks (PINNs), a prominent model in scientific machine learning, uncertainty is typically quantified using Bayesian or dropout methods. However, both approaches suffer from a fundamental limitation: the prior distribution or dropout rate required to construct honest confidence sets cannot be determined without additional information. In this paper, we propose a novel method within the framework of extended fiducial inference (EFI) to provide rigorous uncertainty quantification for PINNs. The proposed method leverages a narrow-neck hyper-network to learn the parameters of the PINN and quantify their uncertainty based on imputed random errors in the observations. This approach overcomes the limitations of Bayesian and dropout methods, enabling the construction of honest confidence sets based solely on observed data. This advancement represents a significant breakthrough for PINNs, greatly enhancing their reliability, interpretability, and applicability to real-world scientific and engineering challenges. Moreover, it establishes a new theoretical framework for EFI, extending its application to large-scale models, eliminating the need for sparse hyper-networks, and significantly improving the automaticity and robustness of statistical inference.

Fast Value Tracking for Deep Reinforcement Learning

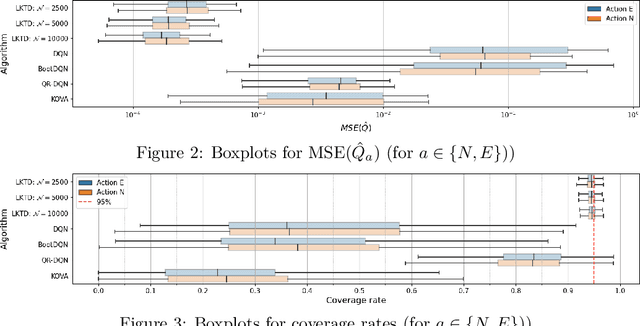
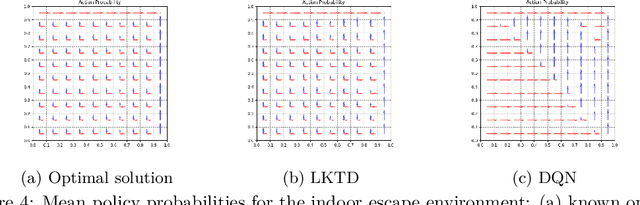
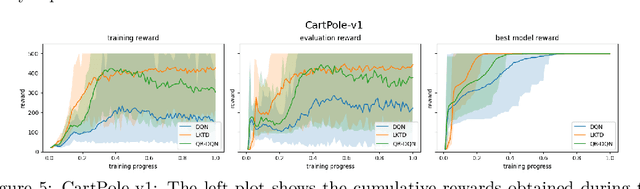
Reinforcement learning (RL) tackles sequential decision-making problems by creating agents that interacts with their environment. However, existing algorithms often view these problem as static, focusing on point estimates for model parameters to maximize expected rewards, neglecting the stochastic dynamics of agent-environment interactions and the critical role of uncertainty quantification. Our research leverages the Kalman filtering paradigm to introduce a novel and scalable sampling algorithm called Langevinized Kalman Temporal-Difference (LKTD) for deep reinforcement learning. This algorithm, grounded in Stochastic Gradient Markov Chain Monte Carlo (SGMCMC), efficiently draws samples from the posterior distribution of deep neural network parameters. Under mild conditions, we prove that the posterior samples generated by the LKTD algorithm converge to a stationary distribution. This convergence not only enables us to quantify uncertainties associated with the value function and model parameters but also allows us to monitor these uncertainties during policy updates throughout the training phase. The LKTD algorithm paves the way for more robust and adaptable reinforcement learning approaches.

Perspective Transformation Layer

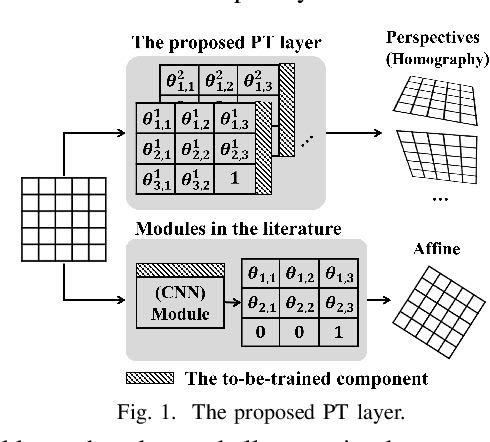
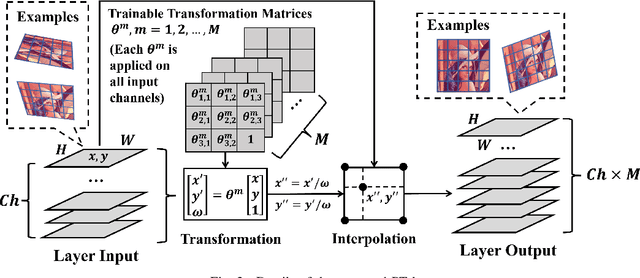
Incorporating geometric transformations that reflect the relative position changes between an observer and an object into computer vision and deep learning models has attracted much attention in recent years. However, the existing proposals mainly focus on affine transformations that cannot fully show viewpoint changes. Furthermore, current solutions often apply a neural network module to learn a single transformation matrix, which ignores the possibility for various viewpoints and creates extra to-be-trained module parameters. In this paper, a layer (PT layer) is proposed to learn the perspective transformations that not only model the geometries in affine transformation but also reflect the viewpoint changes. In addition, being able to be directly trained with gradient descent like traditional layers such as convolutional layers, a single proposed PT layer can learn an adjustable number of multiple viewpoints without training extra module parameters. The experiments and evaluations confirm the superiority of the proposed PT layer.