Doubly Robust Conformalized Survival Analysis with Right-Censored Data

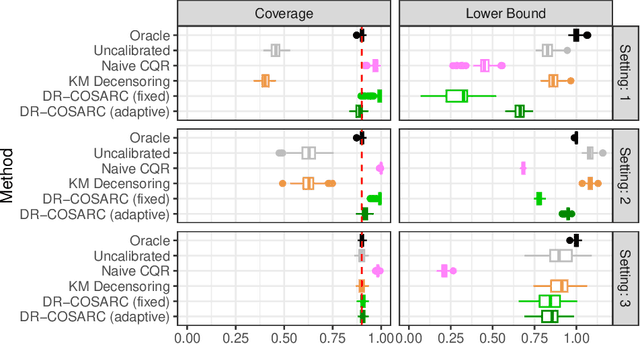
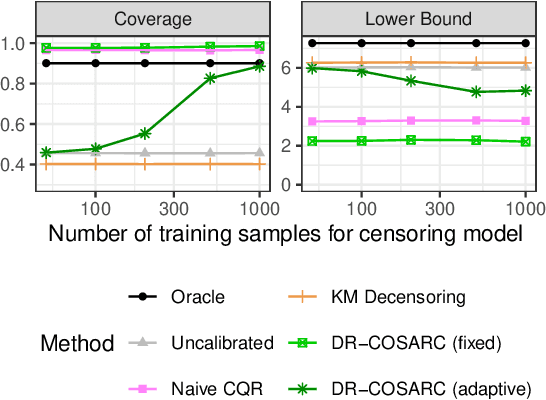
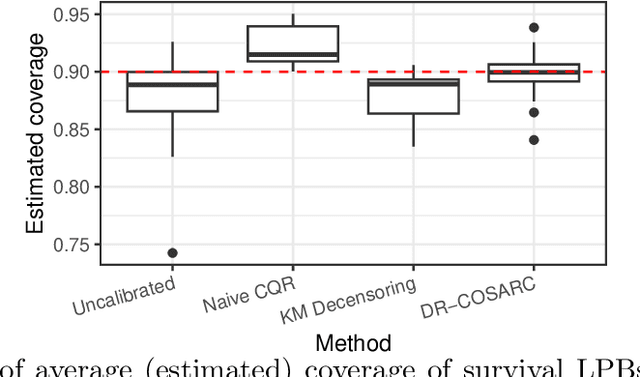
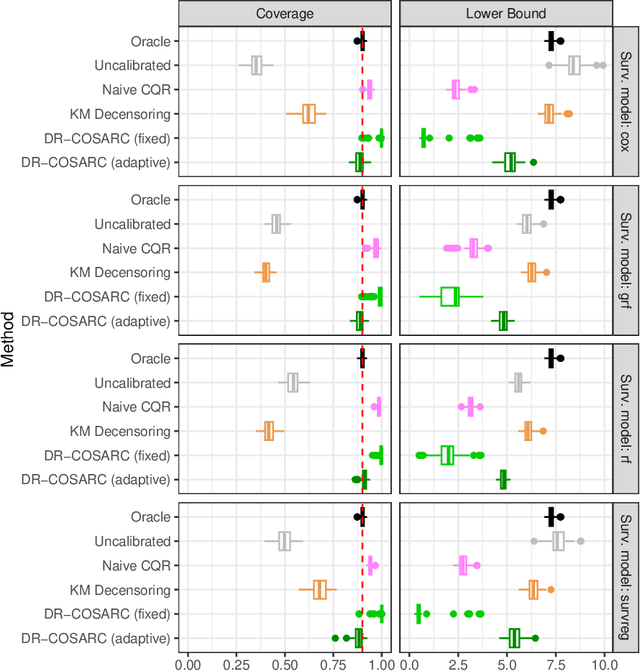
We present a conformal inference method for constructing lower prediction bounds for survival times from right-censored data, extending recent approaches designed for type-I censoring. This method imputes unobserved censoring times using a suitable model, and then analyzes the imputed data using weighted conformal inference. This approach is theoretically supported by an asymptotic double robustness property. Empirical studies on simulated and real data sets demonstrate that our method is more robust than existing approaches in challenging settings where the survival model may be inaccurate, while achieving comparable performance in easier scenarios.

Challenges in Variable Importance Ranking Under Correlation

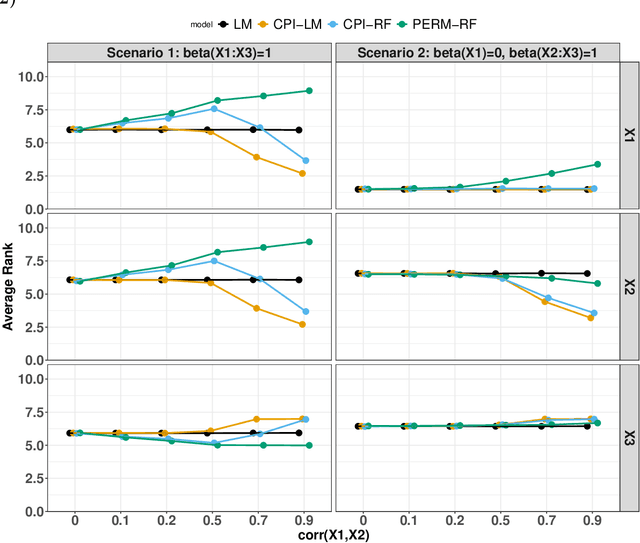
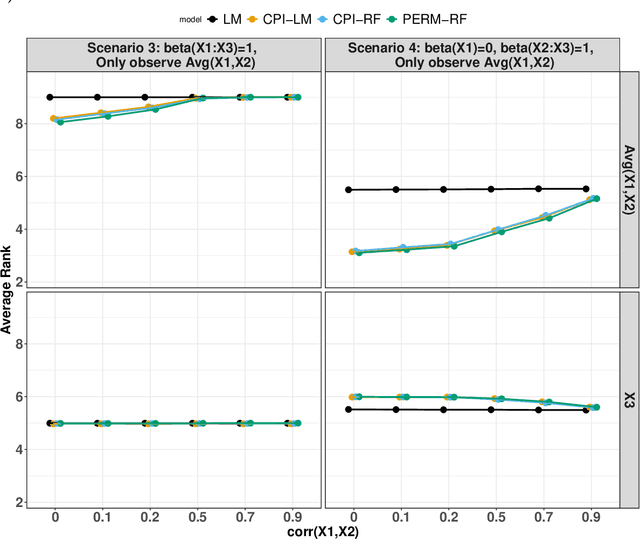
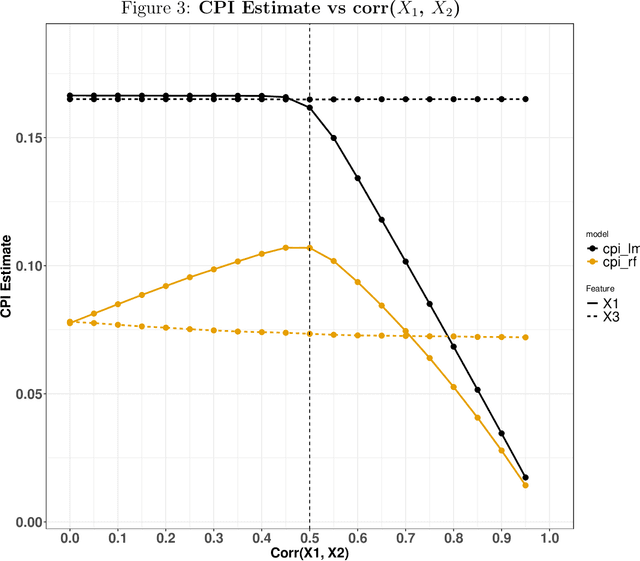
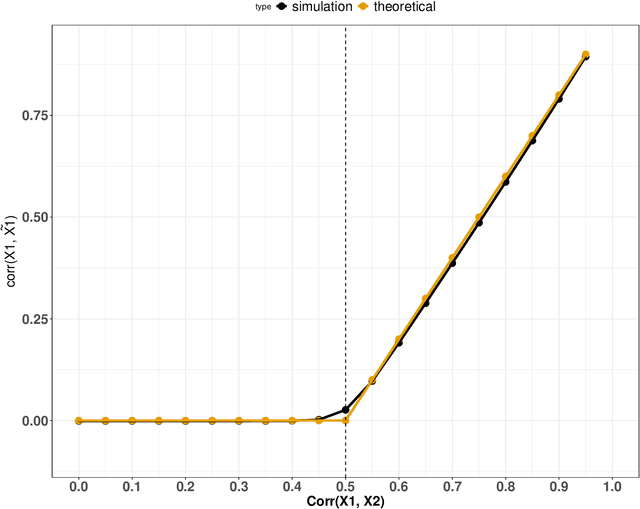
Variable importance plays a pivotal role in interpretable machine learning as it helps measure the impact of factors on the output of the prediction model. Model agnostic methods based on the generation of "null" features via permutation (or related approaches) can be applied. Such analysis is often utilized in pharmaceutical applications due to its ability to interpret black-box models, including tree-based ensembles. A major challenge and significant confounder in variable importance estimation however is the presence of between-feature correlation. Recently, several adjustments to marginal permutation utilizing feature knockoffs were proposed to address this issue, such as the variable importance measure known as conditional predictive impact (CPI). Assessment and evaluation of such approaches is the focus of our work. We first present a comprehensive simulation study investigating the impact of feature correlation on the assessment of variable importance. We then theoretically prove the limitation that highly correlated features pose for the CPI through the knockoff construction. While we expect that there is always no correlation between knockoff variables and its corresponding predictor variables, we prove that the correlation increases linearly beyond a certain correlation threshold between the predictor variables. Our findings emphasize the absence of free lunch when dealing with high feature correlation, as well as the necessity of understanding the utility and limitations behind methods in variable importance estimation.

Development and Evaluation of Conformal Prediction Methods for QSAR

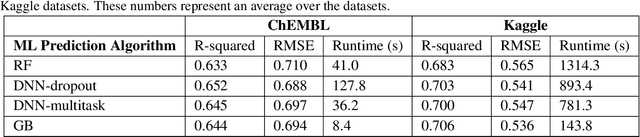
The quantitative structure-activity relationship (QSAR) regression model is a commonly used technique for predicting biological activities of compounds using their molecular descriptors. Predictions from QSAR models can help, for example, to optimize molecular structure; prioritize compounds for further experimental testing; and estimate their toxicity. In addition to the accurate estimation of the activity, it is highly desirable to obtain some estimate of the uncertainty associated with the prediction, e.g., calculate a prediction interval (PI) containing the true molecular activity with a pre-specified probability, say 70%, 90% or 95%. The challenge is that most machine learning (ML) algorithms that achieve superior predictive performance require some add-on methods for estimating uncertainty of their prediction. The development of these algorithms is an active area of research by statistical and ML communities but their implementation for QSAR modeling remains limited. Conformal prediction (CP) is a promising approach. It is agnostic to the prediction algorithm and can produce valid prediction intervals under some weak assumptions on the data distribution. We proposed computationally efficient CP algorithms tailored to the most advanced ML models, including Deep Neural Networks and Gradient Boosting Machines. The validity and efficiency of proposed conformal predictors are demonstrated on a diverse collection of QSAR datasets as well as simulation studies.

The Reciprocal Bayesian LASSO

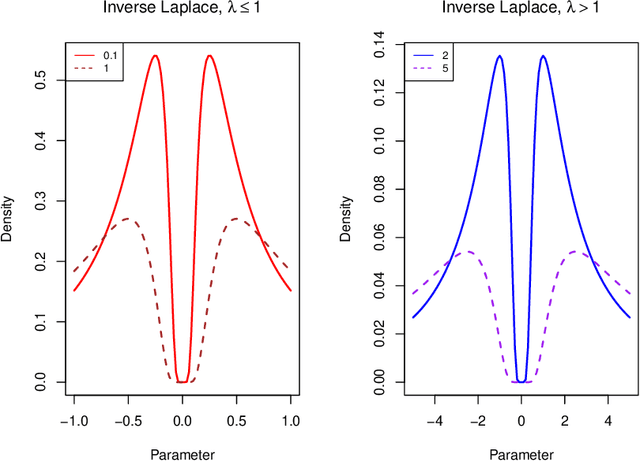
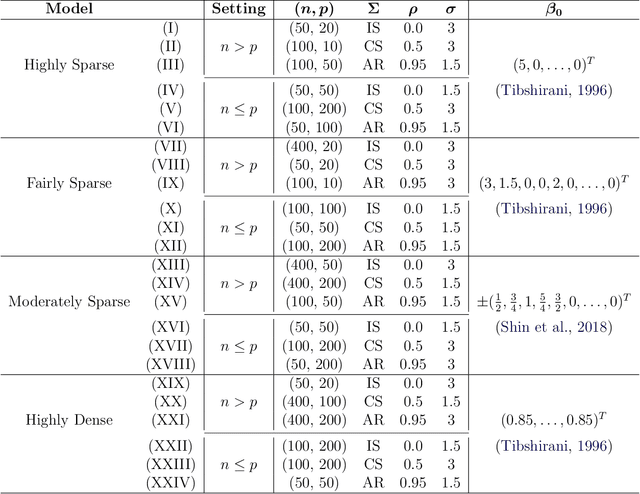
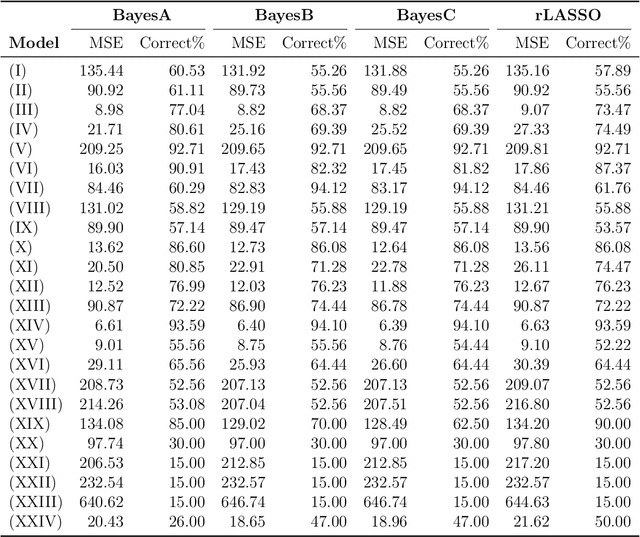
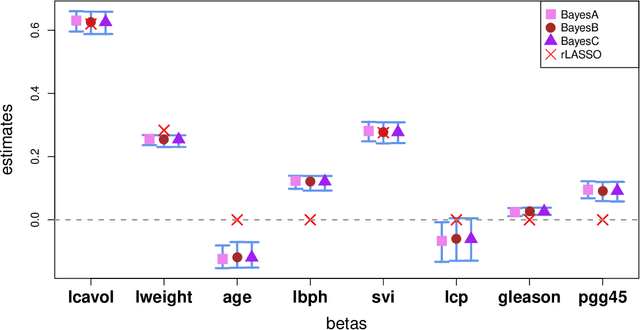
A reciprocal LASSO (rLASSO) regularization employs a decreasing penalty function as opposed to conventional penalization methods that use increasing penalties on the coefficients, leading to stronger parsimony and superior model selection relative to traditional shrinkage methods. Here we consider a fully Bayesian formulation of the rLASSO problem, which is based on the observation that the rLASSO estimate for linear regression parameters can be interpreted as a Bayesian posterior mode estimate when the regression parameters are assigned independent inverse Laplace priors. Bayesian inference from this posterior is possible using an expanded hierarchy motivated by a scale mixture of double Pareto or truncated normal distributions. On simulated and real datasets, we show that the Bayesian formulation outperforms its classical cousin in estimation, prediction, and variable selection across a wide range of scenarios while offering the advantage of posterior inference. Finally, we discuss other variants of this new approach and provide a unified framework for variable selection using flexible reciprocal penalties. All methods described in this paper are publicly available as an R package at: https://github.com/himelmallick/BayesRecipe.