Himel Mallick
Bayesian Joint Additive Factor Models for Multiview Learning
Jun 02, 2024Abstract:It is increasingly common in a wide variety of applied settings to collect data of multiple different types on the same set of samples. Our particular focus in this article is on studying relationships between such multiview features and responses. A motivating application arises in the context of precision medicine where multi-omics data are collected to correlate with clinical outcomes. It is of interest to infer dependence within and across views while combining multimodal information to improve the prediction of outcomes. The signal-to-noise ratio can vary substantially across views, motivating more nuanced statistical tools beyond standard late and early fusion. This challenge comes with the need to preserve interpretability, select features, and obtain accurate uncertainty quantification. We propose a joint additive factor regression model (JAFAR) with a structured additive design, accounting for shared and view-specific components. We ensure identifiability via a novel dependent cumulative shrinkage process (D-CUSP) prior. We provide an efficient implementation via a partially collapsed Gibbs sampler and extend our approach to allow flexible feature and outcome distributions. Prediction of time-to-labor onset from immunome, metabolome, and proteome data illustrates performance gains against state-of-the-art competitors. Our open-source software (R package) is available at https://github.com/niccoloanceschi/jafar.
The Reciprocal Bayesian LASSO
Jan 23, 2020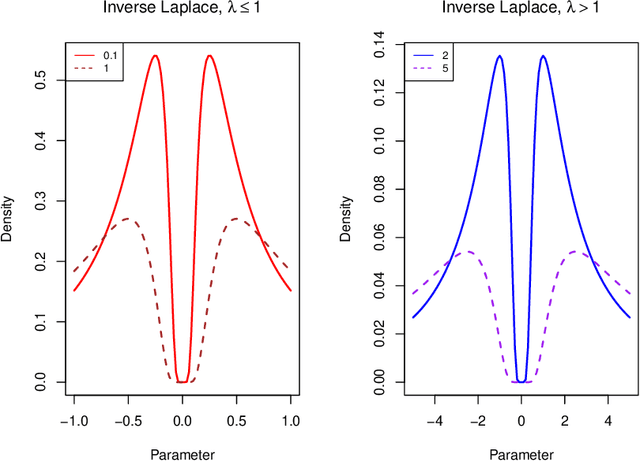
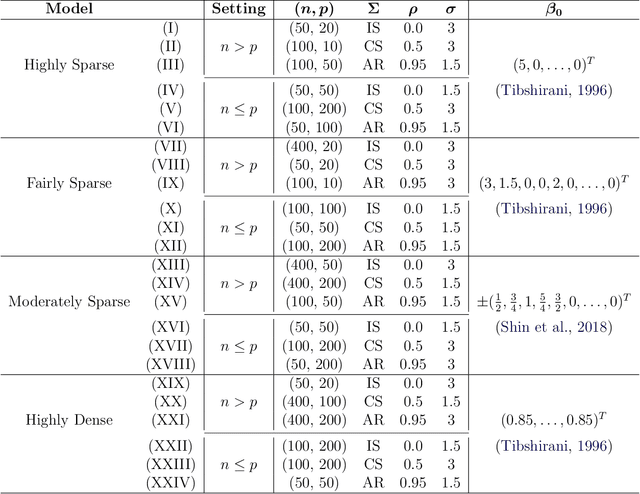
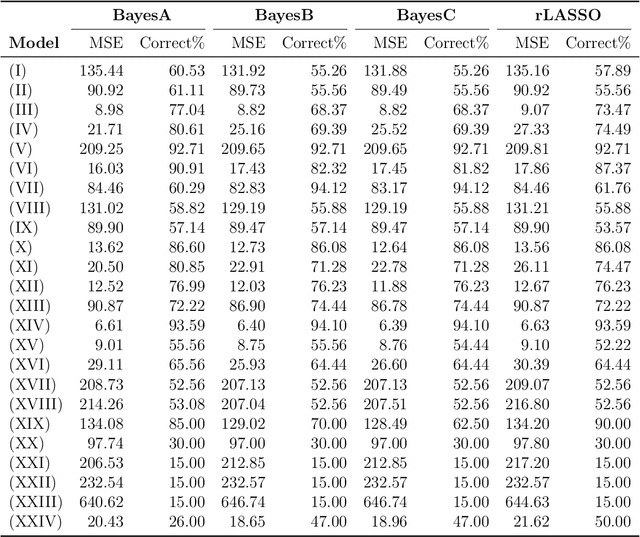
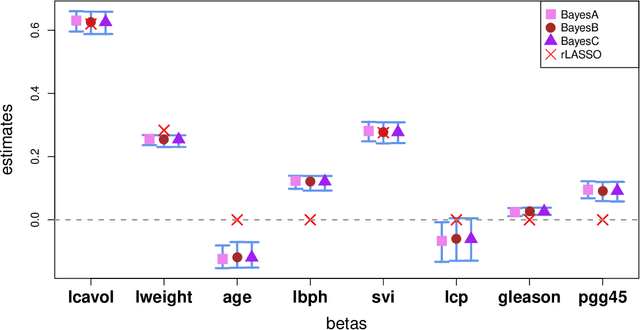
Abstract:A reciprocal LASSO (rLASSO) regularization employs a decreasing penalty function as opposed to conventional penalization methods that use increasing penalties on the coefficients, leading to stronger parsimony and superior model selection relative to traditional shrinkage methods. Here we consider a fully Bayesian formulation of the rLASSO problem, which is based on the observation that the rLASSO estimate for linear regression parameters can be interpreted as a Bayesian posterior mode estimate when the regression parameters are assigned independent inverse Laplace priors. Bayesian inference from this posterior is possible using an expanded hierarchy motivated by a scale mixture of double Pareto or truncated normal distributions. On simulated and real datasets, we show that the Bayesian formulation outperforms its classical cousin in estimation, prediction, and variable selection across a wide range of scenarios while offering the advantage of posterior inference. Finally, we discuss other variants of this new approach and provide a unified framework for variable selection using flexible reciprocal penalties. All methods described in this paper are publicly available as an R package at: https://github.com/himelmallick/BayesRecipe.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge