Optimal and Myopic Information Acquisition
Paper and Code
May 14, 2018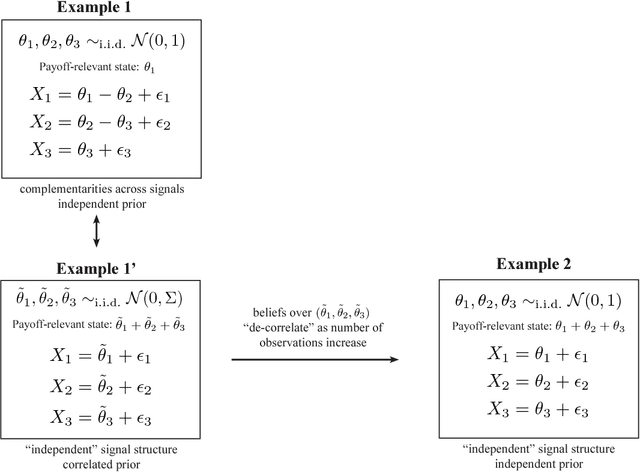

We consider the problem of optimal dynamic information acquisition from many correlated information sources. Each period, the decision-maker jointly takes an action and allocates a fixed number of observations across the available sources. His payoff depends on the actions taken and on an unknown state. In the canonical setting of jointly normal information sources, we show that the optimal dynamic information acquisition rule proceeds myopically after finitely many periods. If signals are acquired in large blocks each period, then the optimal rule turns out to be myopic from period 1. These results demonstrate the possibility of robust and "simple" optimal information acquisition, and simplify the analysis of dynamic information acquisition in a widely used informational environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge