Cheng Gao
MEIC-DT: Memory-Efficient Incremental Clustering for Long-Text Coreference Resolution with Dual-Threshold Constraints
Dec 31, 2025Abstract:In the era of large language models (LLMs), supervised neural methods remain the state-of-the-art (SOTA) for Coreference Resolution. Yet, their full potential is underexplored, particularly in incremental clustering, which faces the critical challenge of balancing efficiency with performance for long texts. To address the limitation, we propose \textbf{MEIC-DT}, a novel dual-threshold, memory-efficient incremental clustering approach based on a lightweight Transformer. MEIC-DT features a dual-threshold constraint mechanism designed to precisely control the Transformer's input scale within a predefined memory budget. This mechanism incorporates a Statistics-Aware Eviction Strategy (\textbf{SAES}), which utilizes distinct statistical profiles from the training and inference phases for intelligent cache management. Furthermore, we introduce an Internal Regularization Policy (\textbf{IRP}) that strategically condenses clusters by selecting the most representative mentions, thereby preserving semantic integrity. Extensive experiments on common benchmarks demonstrate that MEIC-DT achieves highly competitive coreference performance under stringent memory constraints.
Teaching Large Language Models to Maintain Contextual Faithfulness via Synthetic Tasks and Reinforcement Learning
May 22, 2025Abstract:Teaching large language models (LLMs) to be faithful in the provided context is crucial for building reliable information-seeking systems. Therefore, we propose a systematic framework, CANOE, to improve the faithfulness of LLMs in both short-form and long-form generation tasks without human annotations. Specifically, we first synthesize short-form question-answering (QA) data with four diverse tasks to construct high-quality and easily verifiable training data without human annotation. Also, we propose Dual-GRPO, a rule-based reinforcement learning method that includes three tailored rule-based rewards derived from synthesized short-form QA data, while simultaneously optimizing both short-form and long-form response generation. Notably, Dual-GRPO eliminates the need to manually label preference data to train reward models and avoids over-optimizing short-form generation when relying only on the synthesized short-form QA data. Experimental results show that CANOE greatly improves the faithfulness of LLMs across 11 different downstream tasks, even outperforming the most advanced LLMs, e.g., GPT-4o and OpenAI o1.
GLTW: Joint Improved Graph Transformer and LLM via Three-Word Language for Knowledge Graph Completion
Feb 17, 2025Abstract:Knowledge Graph Completion (KGC), which aims to infer missing or incomplete facts, is a crucial task for KGs. However, integrating the vital structural information of KGs into Large Language Models (LLMs) and outputting predictions deterministically remains challenging. To address this, we propose a new method called GLTW, which encodes the structural information of KGs and merges it with LLMs to enhance KGC performance. Specifically, we introduce an improved Graph Transformer (iGT) that effectively encodes subgraphs with both local and global structural information and inherits the characteristics of language model, bypassing training from scratch. Also, we develop a subgraph-based multi-classification training objective, using all entities within KG as classification objects, to boost learning efficiency.Importantly, we combine iGT with an LLM that takes KG language prompts as input.Our extensive experiments on various KG datasets show that GLTW achieves significant performance gains compared to SOTA baselines.
Aligning Large Language Models to Follow Instructions and Hallucinate Less via Effective Data Filtering
Feb 11, 2025Abstract:Training LLMs on data that contains unfamiliar knowledge during the instruction tuning stage can make LLMs overconfident and encourage hallucinations. To address this challenge, we introduce a novel framework, NOVA, which identifies high-quality data that aligns well with the LLM's learned knowledge to reduce hallucinations. NOVA includes Internal Consistency Probing (ICP) and Semantic Equivalence Identification (SEI) to measure how familiar the LLM is with instruction data. Specifically, ICP evaluates the LLM's understanding of the given instruction by calculating the tailored consistency among multiple self-generated responses. SEI further assesses the familiarity of the LLM with the target response by comparing it to the generated responses, using the proposed semantic clustering and well-designed voting strategy. Finally, we introduce an expert-aligned reward model, considering characteristics beyond just familiarity to enhance data quality. By considering data quality and avoiding unfamiliar data, we can utilize the selected data to effectively align LLMs to follow instructions and hallucinate less. Extensive experiments and analysis show that NOVA significantly reduces hallucinations and allows LLMs to maintain a strong ability to follow instructions.
One-Layer Transformer Provably Learns One-Nearest Neighbor In Context
Nov 16, 2024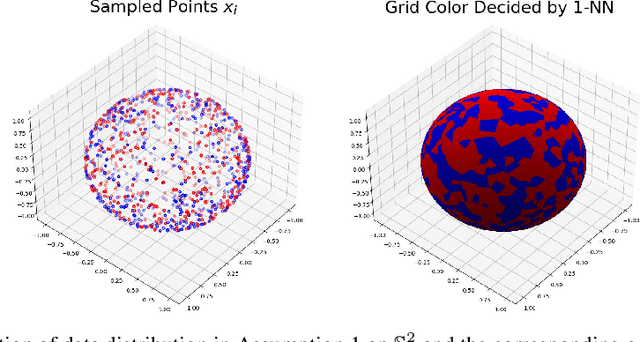
Abstract:Transformers have achieved great success in recent years. Interestingly, transformers have shown particularly strong in-context learning capability -- even without fine-tuning, they are still able to solve unseen tasks well purely based on task-specific prompts. In this paper, we study the capability of one-layer transformers in learning one of the most classical nonparametric estimators, the one-nearest neighbor prediction rule. Under a theoretical framework where the prompt contains a sequence of labeled training data and unlabeled test data, we show that, although the loss function is nonconvex when trained with gradient descent, a single softmax attention layer can successfully learn to behave like a one-nearest neighbor classifier. Our result gives a concrete example of how transformers can be trained to implement nonparametric machine learning algorithms, and sheds light on the role of softmax attention in transformer models.
Global Convergence in Training Large-Scale Transformers
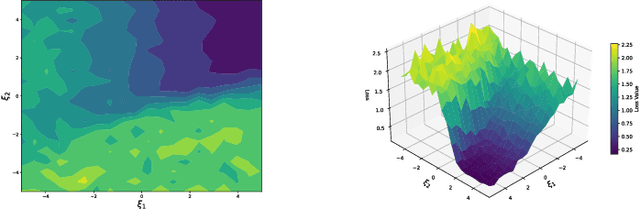
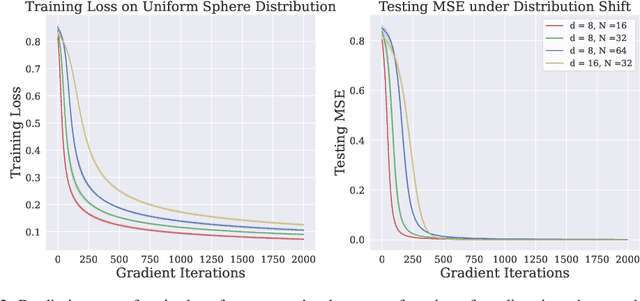
Oct 31, 2024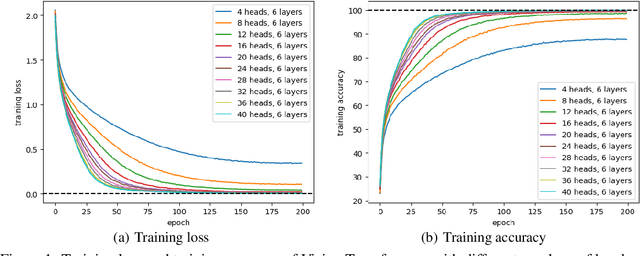
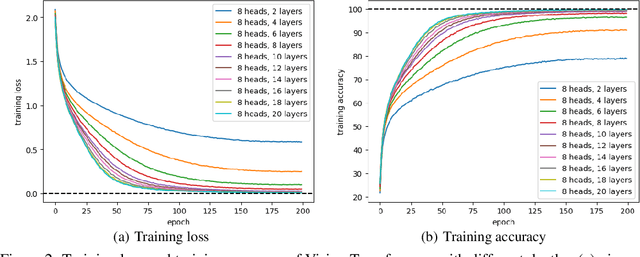
Abstract:Despite the widespread success of Transformers across various domains, their optimization guarantees in large-scale model settings are not well-understood. This paper rigorously analyzes the convergence properties of gradient flow in training Transformers with weight decay regularization. First, we construct the mean-field limit of large-scale Transformers, showing that as the model width and depth go to infinity, gradient flow converges to the Wasserstein gradient flow, which is represented by a partial differential equation. Then, we demonstrate that the gradient flow reaches a global minimum consistent with the PDE solution when the weight decay regularization parameter is sufficiently small. Our analysis is based on a series of novel mean-field techniques that adapt to Transformers. Compared with existing tools for deep networks (Lu et al., 2020) that demand homogeneity and global Lipschitz smoothness, we utilize a refined analysis assuming only $\textit{partial homogeneity}$ and $\textit{local Lipschitz smoothness}$. These new techniques may be of independent interest.
Enhancing Legal Case Retrieval via Scaling High-quality Synthetic Query-Candidate Pairs
Oct 09, 2024

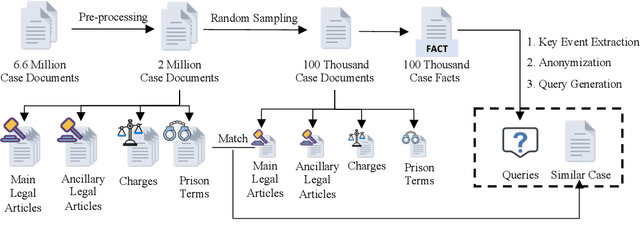

Abstract:Legal case retrieval (LCR) aims to provide similar cases as references for a given fact description. This task is crucial for promoting consistent judgments in similar cases, effectively enhancing judicial fairness and improving work efficiency for judges. However, existing works face two main challenges for real-world applications: existing works mainly focus on case-to-case retrieval using lengthy queries, which does not match real-world scenarios; and the limited data scale, with current datasets containing only hundreds of queries, is insufficient to satisfy the training requirements of existing data-hungry neural models. To address these issues, we introduce an automated method to construct synthetic query-candidate pairs and build the largest LCR dataset to date, LEAD, which is hundreds of times larger than existing datasets. This data construction method can provide ample training signals for LCR models. Experimental results demonstrate that model training with our constructed data can achieve state-of-the-art results on two widely-used LCR benchmarks. Besides, the construction method can also be applied to civil cases and achieve promising results. The data and codes can be found in https://github.com/thunlp/LEAD.
Robust Transfer Learning with Unreliable Source Data
Oct 06, 2023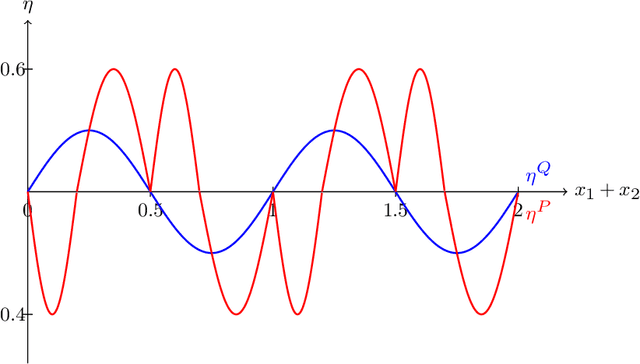

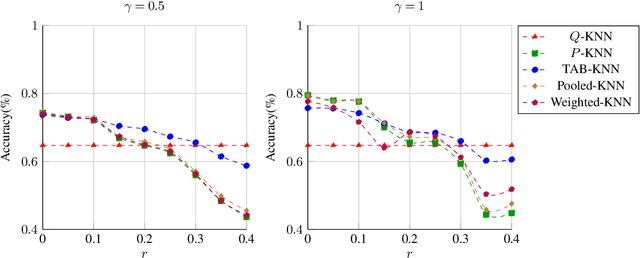
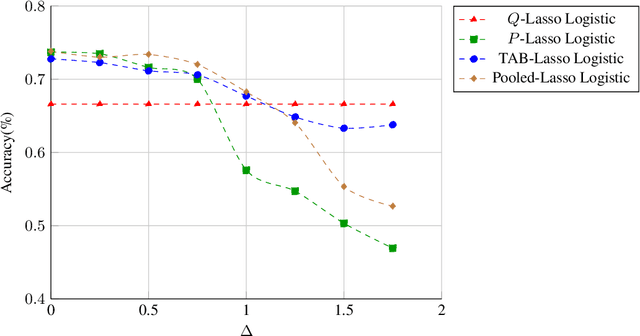
Abstract:This paper addresses challenges in robust transfer learning stemming from ambiguity in Bayes classifiers and weak transferable signals between the target and source distribution. We introduce a novel quantity called the ''ambiguity level'' that measures the discrepancy between the target and source regression functions, propose a simple transfer learning procedure, and establish a general theorem that shows how this new quantity is related to the transferability of learning in terms of risk improvements. Our proposed ''Transfer Around Boundary'' (TAB) model, with a threshold balancing the performance of target and source data, is shown to be both efficient and robust, improving classification while avoiding negative transfer. Moreover, we demonstrate the effectiveness of the TAB model on non-parametric classification and logistic regression tasks, achieving upper bounds which are optimal up to logarithmic factors. Simulation studies lend further support to the effectiveness of TAB. We also provide simple approaches to bound the excess misclassification error without the need for specialized knowledge in transfer learning.
Blending Knowledge in Deep Recurrent Networks for Adverse Event Prediction at Hospital Discharge
Apr 09, 2021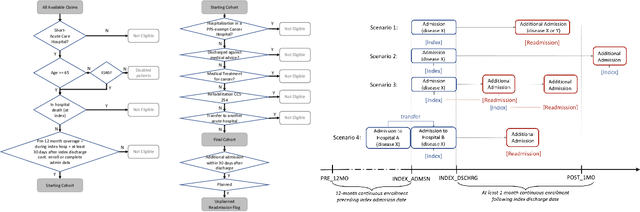
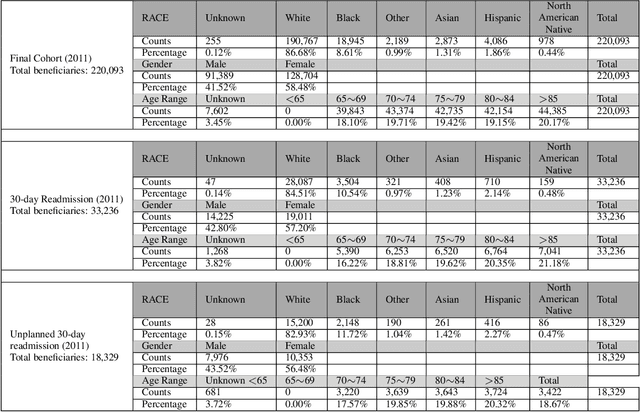
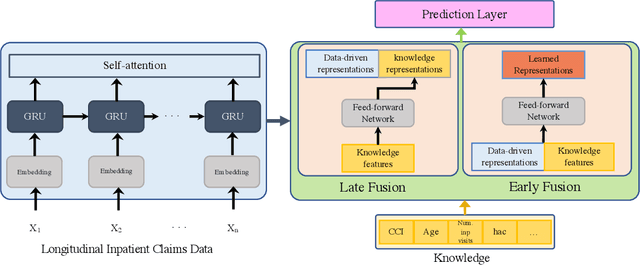

Abstract:Deep learning architectures have an extremely high-capacity for modeling complex data in a wide variety of domains. However, these architectures have been limited in their ability to support complex prediction problems using insurance claims data, such as readmission at 30 days, mainly due to data sparsity issue. Consequently, classical machine learning methods, especially those that embed domain knowledge in handcrafted features, are often on par with, and sometimes outperform, deep learning approaches. In this paper, we illustrate how the potential of deep learning can be achieved by blending domain knowledge within deep learning architectures to predict adverse events at hospital discharge, including readmissions. More specifically, we introduce a learning architecture that fuses a representation of patient data computed by a self-attention based recurrent neural network, with clinically relevant features. We conduct extensive experiments on a large claims dataset and show that the blended method outperforms the standard machine learning approaches.
The 1st Tiny Object Detection Challenge:Methods and Results
Oct 06, 2020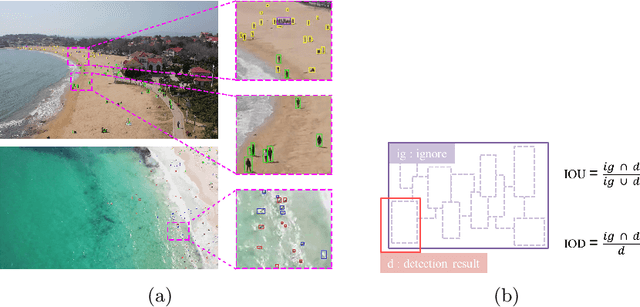
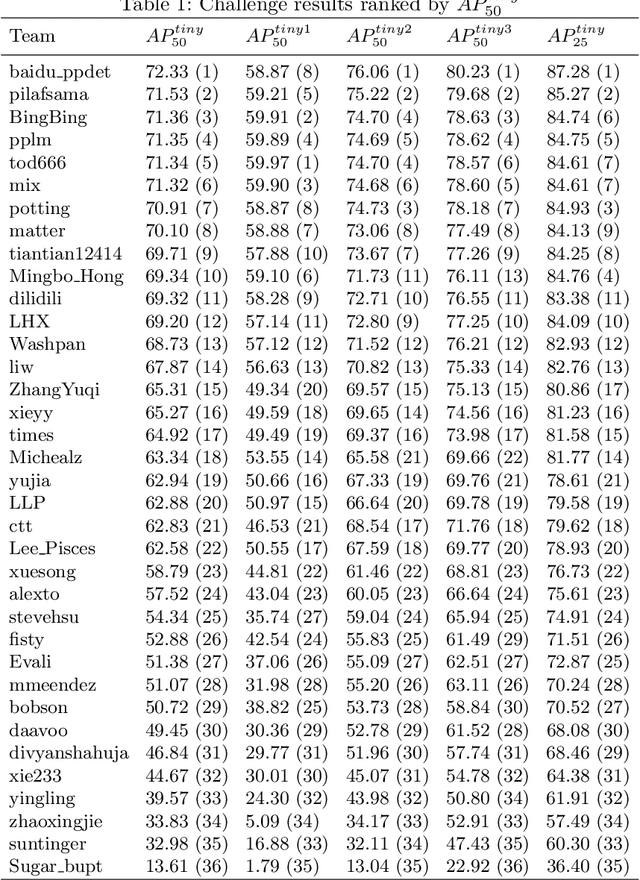
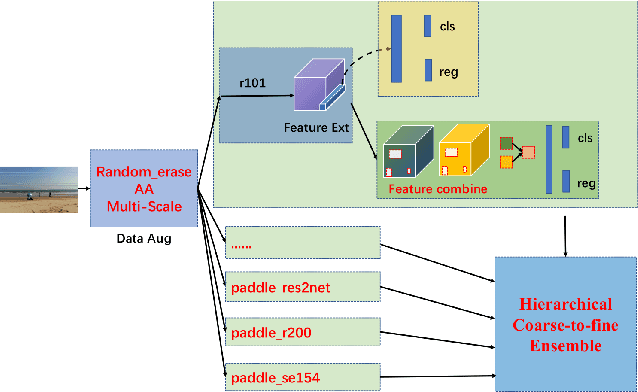

Abstract:The 1st Tiny Object Detection (TOD) Challenge aims to encourage research in developing novel and accurate methods for tiny object detection in images which have wide views, with a current focus on tiny person detection. The TinyPerson dataset was used for the TOD Challenge and is publicly released. It has 1610 images and 72651 box-levelannotations. Around 36 participating teams from the globe competed inthe 1st TOD Challenge. In this paper, we provide a brief summary of the1st TOD Challenge including brief introductions to the top three methods.The submission leaderboard will be reopened for researchers that areinterested in the TOD challenge. The benchmark dataset and other information can be found at: https://github.com/ucas-vg/TinyBenchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge