Yihan He
KernelEvolve: Scaling Agentic Kernel Coding for Heterogeneous AI Accelerators at Meta
Dec 30, 2025Abstract:Making deep learning recommendation model (DLRM) training and inference fast and efficient is important. However, this presents three key system challenges - model architecture diversity, kernel primitive diversity, and hardware generation and architecture heterogeneity. This paper presents KernelEvolve-an agentic kernel coding framework-to tackle heterogeneity at-scale for DLRM. KernelEvolve is designed to take kernel specifications as input and automate the process of kernel generation and optimization for recommendation model across heterogeneous hardware architectures. KernelEvolve does so by operating at multiple programming abstractions, from Triton and CuTe DSL to low-level hardware agnostic languages, spanning the full hardware-software optimization stack. The kernel optimization process is described as graph-based search with selection policy, universal operator, fitness function, and termination rule, dynamically adapts to runtime execution context through retrieval-augmented prompt synthesis. We designed, implemented, and deployed KernelEvolve to optimize a wide variety of production recommendation models across generations of NVIDIA and AMD GPUs, as well as Meta's AI accelerators. We validate KernelEvolve on the publicly-available KernelBench suite, achieving 100% pass rate on all 250 problems across three difficulty levels, and 160 PyTorch ATen operators across three heterogeneous hardware platforms, demonstrating 100% correctness. KernelEvolve reduces development time from weeks to hours and achieves substantial performance improvements over PyTorch baselines across diverse production use cases and for heterogeneous AI systems at-scale. Beyond performance efficiency improvements, KernelEvolve significantly mitigates the programmability barrier for new AI hardware by enabling automated kernel generation for in-house developed AI hardware.
A Novel P-bit-based Probabilistic Computing Approach for Solving the 3-D Protein Folding Problem
Feb 27, 2025Abstract:In the post-Moore era, the need for efficient solutions to non-deterministic polynomial-time (NP) problems is becoming more pressing. In this context, the Ising model implemented by the probabilistic computing systems with probabilistic bits (p-bits) has attracted attention due to the widespread availability of p-bits and support for large-scale simulations. This study marks the first work to apply probabilistic computing to tackle protein folding, a significant NP-complete problem challenge in biology. We represent proteins as sequences of hydrophobic (H) and polar (P) beads within a three-dimensional (3-D) grid and introduce a novel many-body interaction-based encoding method to map the problem onto an Ising model. Our simulations show that this approach significantly simplifies the energy landscape for short peptide sequences of six amino acids, halving the number of energy levels. Furthermore, the proposed mapping method achieves approximately 100 times acceleration for sequences consisting of ten amino acids in identifying the correct folding configuration. We predicted the optimal folding configuration for a peptide sequence of 36 amino acids by identifying the ground state. These findings highlight the unique potential of the proposed encoding method for solving protein folding and, importantly, provide new tools for solving similar NP-complete problems in biology by probabilistic computing approach.
Transformers versus the EM Algorithm in Multi-class Clustering
Feb 09, 2025Abstract:LLMs demonstrate significant inference capacities in complicated machine learning tasks, using the Transformer model as its backbone. Motivated by the limited understanding of such models on the unsupervised learning problems, we study the learning guarantees of Transformers in performing multi-class clustering of the Gaussian Mixture Models. We develop a theory drawing strong connections between the Softmax Attention layers and the workflow of the EM algorithm on clustering the mixture of Gaussians. Our theory provides approximation bounds for the Expectation and Maximization steps by proving the universal approximation abilities of multivariate mappings by Softmax functions. In addition to the approximation guarantees, we also show that with a sufficient number of pre-training samples and an initialization, Transformers can achieve the minimax optimal rate for the problem considered. Our extensive simulations empirically verified our theory by revealing the strong learning capacities of Transformers even beyond the assumptions in the theory, shedding light on the powerful inference capacities of LLMs.
Transformers and Their Roles as Time Series Foundation Models
Feb 05, 2025



Abstract:We give a comprehensive analysis of transformers as time series foundation models, focusing on their approximation and generalization capabilities. First, we demonstrate that there exist transformers that fit an autoregressive model on input univariate time series via gradient descent. We then analyze MOIRAI, a multivariate time series foundation model capable of handling an arbitrary number of covariates. We prove that it is capable of automatically fitting autoregressive models with an arbitrary number of covariates, offering insights into its design and empirical success. For generalization, we establish bounds for pretraining when the data satisfies Dobrushin's condition. Experiments support our theoretical findings, highlighting the efficacy of transformers as time series foundation models.
Transformers Simulate MLE for Sequence Generation in Bayesian Networks
Jan 05, 2025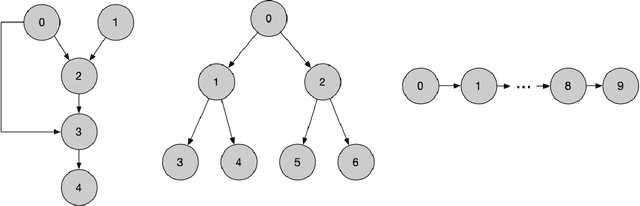

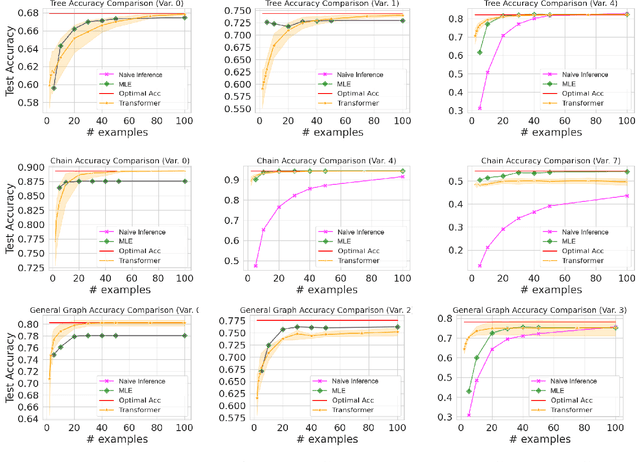
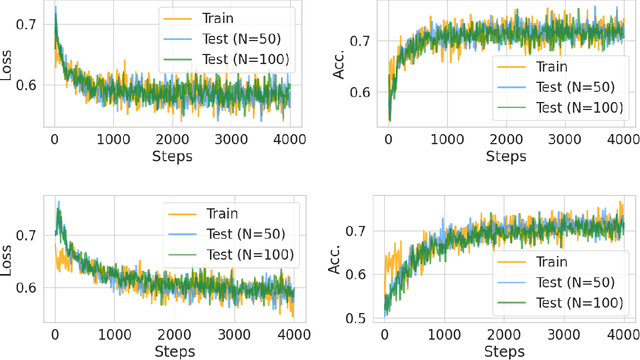
Abstract:Transformers have achieved significant success in various fields, notably excelling in tasks involving sequential data like natural language processing. Despite these achievements, the theoretical understanding of transformers' capabilities remains limited. In this paper, we investigate the theoretical capabilities of transformers to autoregressively generate sequences in Bayesian networks based on in-context maximum likelihood estimation (MLE). Specifically, we consider a setting where a context is formed by a set of independent sequences generated according to a Bayesian network. We demonstrate that there exists a simple transformer model that can (i) estimate the conditional probabilities of the Bayesian network according to the context, and (ii) autoregressively generate a new sample according to the Bayesian network with estimated conditional probabilities. We further demonstrate in extensive experiments that such a transformer does not only exist in theory, but can also be effectively obtained through training. Our analysis highlights the potential of transformers to learn complex probabilistic models and contributes to a better understanding of large language models as a powerful class of sequence generators.
Learning Spectral Methods by Transformers
Jan 05, 2025



Abstract:Transformers demonstrate significant advantages as the building block of modern LLMs. In this work, we study the capacities of Transformers in performing unsupervised learning. We show that multi-layered Transformers, given a sufficiently large set of pre-training instances, are able to learn the algorithms themselves and perform statistical estimation tasks given new instances. This learning paradigm is distinct from the in-context learning setup and is similar to the learning procedure of human brains where skills are learned through past experience. Theoretically, we prove that pre-trained Transformers can learn the spectral methods and use the classification of bi-class Gaussian mixture model as an example. Our proof is constructive using algorithmic design techniques. Our results are built upon the similarities of multi-layered Transformer architecture with the iterative recovery algorithms used in practice. Empirically, we verify the strong capacity of the multi-layered (pre-trained) Transformer on unsupervised learning through the lens of both the PCA and the Clustering tasks performed on the synthetic and real-world datasets.
One-Layer Transformer Provably Learns One-Nearest Neighbor In Context
Nov 16, 2024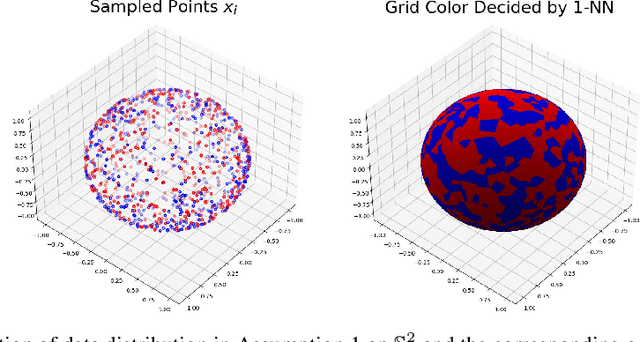
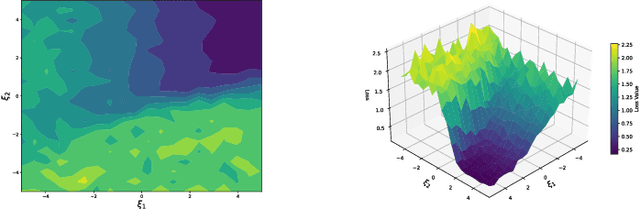
Abstract:Transformers have achieved great success in recent years. Interestingly, transformers have shown particularly strong in-context learning capability -- even without fine-tuning, they are still able to solve unseen tasks well purely based on task-specific prompts. In this paper, we study the capability of one-layer transformers in learning one of the most classical nonparametric estimators, the one-nearest neighbor prediction rule. Under a theoretical framework where the prompt contains a sequence of labeled training data and unlabeled test data, we show that, although the loss function is nonconvex when trained with gradient descent, a single softmax attention layer can successfully learn to behave like a one-nearest neighbor classifier. Our result gives a concrete example of how transformers can be trained to implement nonparametric machine learning algorithms, and sheds light on the role of softmax attention in transformer models.
Global Convergence in Training Large-Scale Transformers
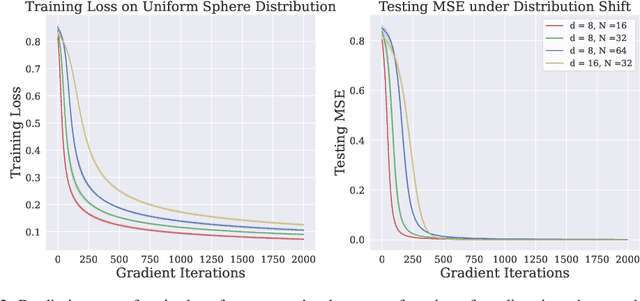
Oct 31, 2024
Abstract:Despite the widespread success of Transformers across various domains, their optimization guarantees in large-scale model settings are not well-understood. This paper rigorously analyzes the convergence properties of gradient flow in training Transformers with weight decay regularization. First, we construct the mean-field limit of large-scale Transformers, showing that as the model width and depth go to infinity, gradient flow converges to the Wasserstein gradient flow, which is represented by a partial differential equation. Then, we demonstrate that the gradient flow reaches a global minimum consistent with the PDE solution when the weight decay regularization parameter is sufficiently small. Our analysis is based on a series of novel mean-field techniques that adapt to Transformers. Compared with existing tools for deep networks (Lu et al., 2020) that demand homogeneity and global Lipschitz smoothness, we utilize a refined analysis assuming only $\textit{partial homogeneity}$ and $\textit{local Lipschitz smoothness}$. These new techniques may be of independent interest.
SafeBench: A Benchmarking Platform for Safety Evaluation of Autonomous Vehicles
Jun 20, 2022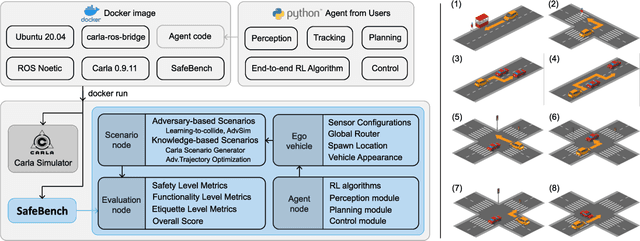
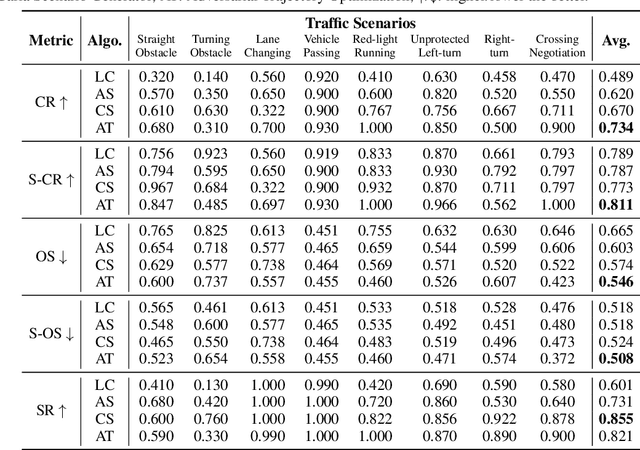
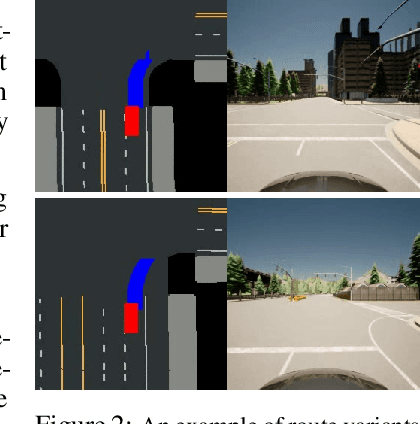

Abstract:As shown by recent studies, machine intelligence-enabled systems are vulnerable to test cases resulting from either adversarial manipulation or natural distribution shifts. This has raised great concerns about deploying machine learning algorithms for real-world applications, especially in the safety-critical domains such as autonomous driving (AD). On the other hand, traditional AD testing on naturalistic scenarios requires hundreds of millions of driving miles due to the high dimensionality and rareness of the safety-critical scenarios in the real world. As a result, several approaches for autonomous driving evaluation have been explored, which are usually, however, based on different simulation platforms, types of safety-critical scenarios, scenario generation algorithms, and driving route variations. Thus, despite a large amount of effort in autonomous driving testing, it is still challenging to compare and understand the effectiveness and efficiency of different testing scenario generation algorithms and testing mechanisms under similar conditions. In this paper, we aim to provide the first unified platform SafeBench to integrate different types of safety-critical testing scenarios, scenario generation algorithms, and other variations such as driving routes and environments. Meanwhile, we implement 4 deep reinforcement learning-based AD algorithms with 4 types of input (e.g., bird's-eye view, camera) to perform fair comparisons on SafeBench. We find our generated testing scenarios are indeed more challenging and observe the trade-off between the performance of AD agents under benign and safety-critical testing scenarios. We believe our unified platform SafeBench for large-scale and effective autonomous driving testing will motivate the development of new testing scenario generation and safe AD algorithms. SafeBench is available at https://safebench.github.io.
Multi-fidelity Stability for Graph Representation Learning
Nov 25, 2021Abstract:In the problem of structured prediction with graph representation learning (GRL for short), the hypothesis returned by the algorithm maps the set of features in the \emph{receptive field} of the targeted vertex to its label. To understand the learnability of those algorithms, we introduce a weaker form of uniform stability termed \emph{multi-fidelity stability} and give learning guarantees for weakly dependent graphs. We testify that ~\citet{london2016stability}'s claim on the generalization of a single sample holds for GRL when the receptive field is sparse. In addition, we study the stability induced bound for two popular algorithms: \textbf{(1)} Stochastic gradient descent under convex and non-convex landscape. In this example, we provide non-asymptotic bounds that highly depend on the sparsity of the receptive field constructed by the algorithm. \textbf{(2)} The constrained regression problem on a 1-layer linear equivariant GNN. In this example, we present lower bounds for the discrepancy between the two types of stability, which justified the multi-fidelity design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge