Block-Randomized Stochastic Proximal Gradient for Low-Rank Tensor Factorization

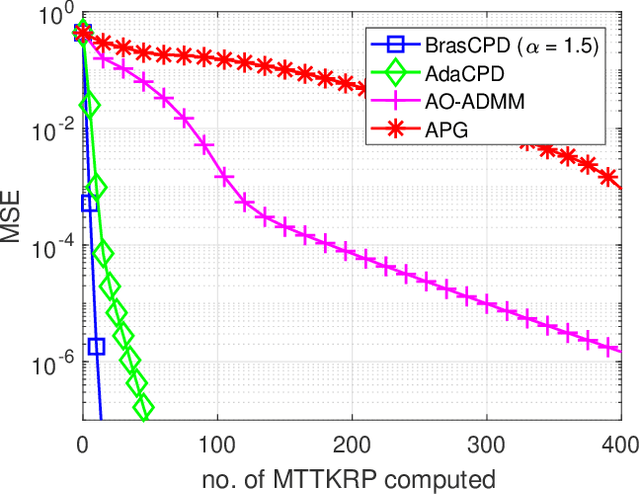
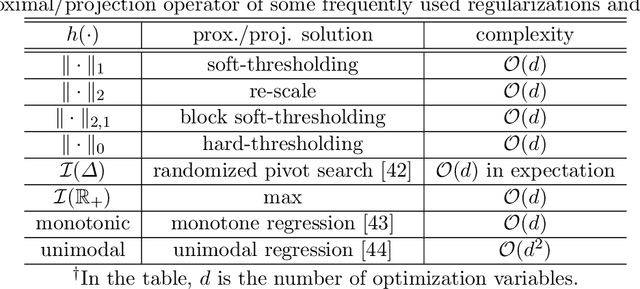
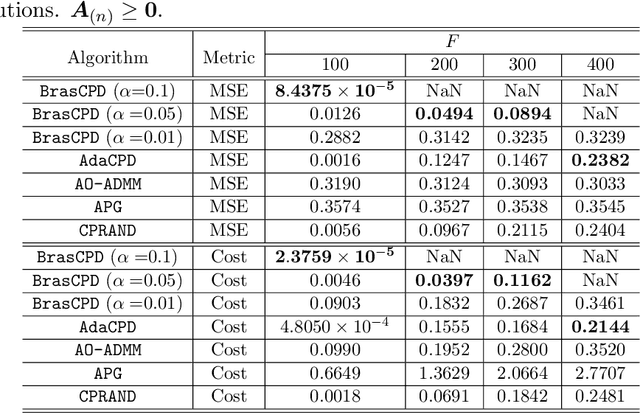
This work considers the problem of computing the \textit{canonical polyadic decomposition} (CPD) of large tensors. Prior works mostly leverage data sparsity to handle this problem, which are not suitable for handling dense tensors that often arise in applications such as medical imaging, computer vision, and remote sensing. Stochastic optimization is known for its low memory cost and per-iteration complexity when handling dense data. However, existing stochastic CPD algorithms are hard to incorporate a variety of constraints and regularizations that are of interest in signal and data analytics. Convergence properties of many such algorithms are also unclear. In this work, we propose a stochastic optimization framework for large-scale CPD with constraints/regularizations. The framework works under a doubly randomized fashion, and can be regarded as a judicious combination of \textit{randomized block coordinate descent} (BCD) and \textit{stochastic proximal gradient} (SPG). The algorithm enjoys lightweight updates and small memory footprint, and thus scales well. In addition, this framework entails considerable flexibility---many frequently used regularizers and constraints can be readily handled under the proposed scheme. The approach is also supported by convergence analysis. Numerical results on large-scale dense tensors are employed to showcase the effectiveness of the proposed approach.