Decoding Game: On Minimax Optimality of Heuristic Text Generation Strategies
Paper and Code
Oct 04, 2024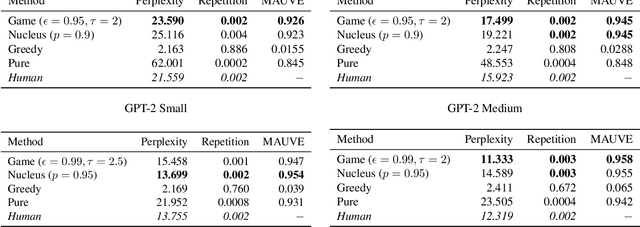
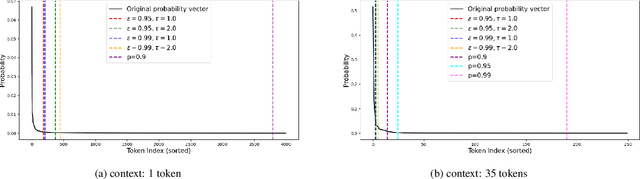
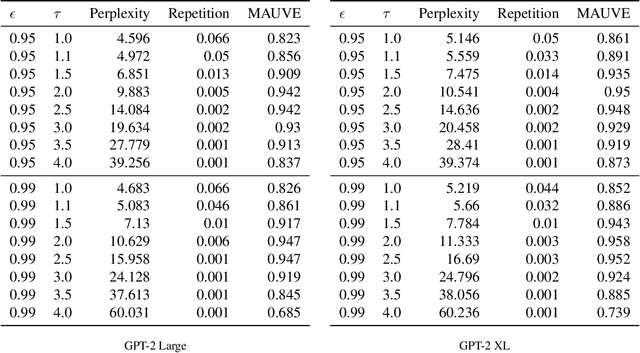
Decoding strategies play a pivotal role in text generation for modern language models, yet a puzzling gap divides theory and practice. Surprisingly, strategies that should intuitively be optimal, such as Maximum a Posteriori (MAP), often perform poorly in practice. Meanwhile, popular heuristic approaches like Top-$k$ and Nucleus sampling, which employ truncation and normalization of the conditional next-token probabilities, have achieved great empirical success but lack theoretical justifications. In this paper, we propose Decoding Game, a comprehensive theoretical framework which reimagines text generation as a two-player zero-sum game between Strategist, who seeks to produce text credible in the true distribution, and Nature, who distorts the true distribution adversarially. After discussing the decomposibility of multi-step generation, we derive the optimal strategy in closed form for one-step Decoding Game. It is shown that the adversarial Nature imposes an implicit regularization on likelihood maximization, and truncation-normalization methods are first-order approximations to the optimal strategy under this regularization. Additionally, by generalizing the objective and parameters of Decoding Game, near-optimal strategies encompass diverse methods such as greedy search, temperature scaling, and hybrids thereof. Numerical experiments are conducted to complement our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge