Omar Hagrass
Decoding Game: On Minimax Optimality of Heuristic Text Generation Strategies
Oct 04, 2024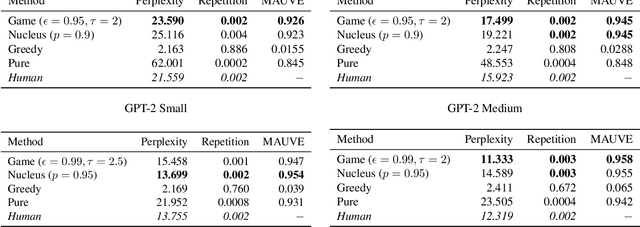
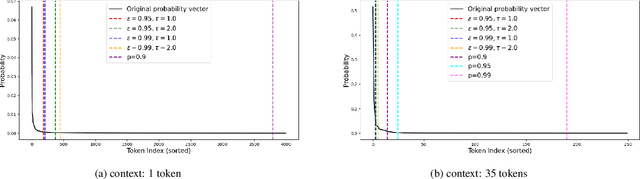
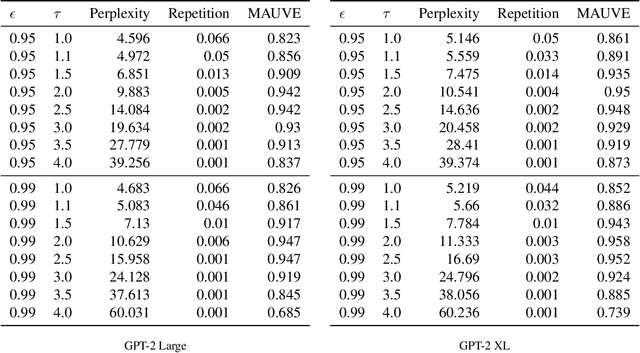
Abstract:Decoding strategies play a pivotal role in text generation for modern language models, yet a puzzling gap divides theory and practice. Surprisingly, strategies that should intuitively be optimal, such as Maximum a Posteriori (MAP), often perform poorly in practice. Meanwhile, popular heuristic approaches like Top-$k$ and Nucleus sampling, which employ truncation and normalization of the conditional next-token probabilities, have achieved great empirical success but lack theoretical justifications. In this paper, we propose Decoding Game, a comprehensive theoretical framework which reimagines text generation as a two-player zero-sum game between Strategist, who seeks to produce text credible in the true distribution, and Nature, who distorts the true distribution adversarially. After discussing the decomposibility of multi-step generation, we derive the optimal strategy in closed form for one-step Decoding Game. It is shown that the adversarial Nature imposes an implicit regularization on likelihood maximization, and truncation-normalization methods are first-order approximations to the optimal strategy under this regularization. Additionally, by generalizing the objective and parameters of Decoding Game, near-optimal strategies encompass diverse methods such as greedy search, temperature scaling, and hybrids thereof. Numerical experiments are conducted to complement our theoretical analysis.
Minimax Optimal Goodness-of-Fit Testing with Kernel Stein Discrepancy
Apr 12, 2024



Abstract:We explore the minimax optimality of goodness-of-fit tests on general domains using the kernelized Stein discrepancy (KSD). The KSD framework offers a flexible approach for goodness-of-fit testing, avoiding strong distributional assumptions, accommodating diverse data structures beyond Euclidean spaces, and relying only on partial knowledge of the reference distribution, while maintaining computational efficiency. We establish a general framework and an operator-theoretic representation of the KSD, encompassing many existing KSD tests in the literature, which vary depending on the domain. We reveal the characteristics and limitations of KSD and demonstrate its non-optimality under a certain alternative space, defined over general domains when considering $\chi^2$-divergence as the separation metric. To address this issue of non-optimality, we propose a modified, minimax optimal test by incorporating a spectral regularizer, thereby overcoming the shortcomings of standard KSD tests. Our results are established under a weak moment condition on the Stein kernel, which relaxes the bounded kernel assumption required by prior work in the analysis of kernel-based hypothesis testing. Additionally, we introduce an adaptive test capable of achieving minimax optimality up to a logarithmic factor by adapting to unknown parameters. Through numerical experiments, we illustrate the superior performance of our proposed tests across various domains compared to their unregularized counterparts.
Spectral Regularized Kernel Goodness-of-Fit Tests
Aug 08, 2023



Abstract:Maximum mean discrepancy (MMD) has enjoyed a lot of success in many machine learning and statistical applications, including non-parametric hypothesis testing, because of its ability to handle non-Euclidean data. Recently, it has been demonstrated in Balasubramanian et al.(2021) that the goodness-of-fit test based on MMD is not minimax optimal while a Tikhonov regularized version of it is, for an appropriate choice of the regularization parameter. However, the results in Balasubramanian et al. (2021) are obtained under the restrictive assumptions of the mean element being zero, and the uniform boundedness condition on the eigenfunctions of the integral operator. Moreover, the test proposed in Balasubramanian et al. (2021) is not practical as it is not computable for many kernels. In this paper, we address these shortcomings and extend the results to general spectral regularizers that include Tikhonov regularization.
Spectral Regularized Kernel Two-Sample Tests
Dec 19, 2022



Abstract:Over the last decade, an approach that has gained a lot of popularity to tackle non-parametric testing problems on general (i.e., non-Euclidean) domains is based on the notion of reproducing kernel Hilbert space (RKHS) embedding of probability distributions. The main goal of our work is to understand the optimality of two-sample tests constructed based on this approach. First, we show that the popular MMD (maximum mean discrepancy) two-sample test is not optimal in terms of the separation boundary measured in Hellinger distance. Second, we propose a modification to the MMD test based on spectral regularization by taking into account the covariance information (which is not captured by the MMD test) and prove the proposed test to be minimax optimal with a smaller separation boundary than that achieved by the MMD test. Third, we propose an adaptive version of the above test which involves a data-driven strategy to choose the regularization parameter and show the adaptive test to be almost minimax optimal up to a logarithmic factor. Moreover, our results hold for the permutation variant of the test where the test threshold is chosen elegantly through the permutation of the samples. Through numerical experiments on synthetic and real-world data, we demonstrate the superior performance of the proposed test in comparison to the MMD test.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge