Minimax Optimal Goodness-of-Fit Testing with Kernel Stein Discrepancy

We explore the minimax optimality of goodness-of-fit tests on general domains using the kernelized Stein discrepancy (KSD). The KSD framework offers a flexible approach for goodness-of-fit testing, avoiding strong distributional assumptions, accommodating diverse data structures beyond Euclidean spaces, and relying only on partial knowledge of the reference distribution, while maintaining computational efficiency. We establish a general framework and an operator-theoretic representation of the KSD, encompassing many existing KSD tests in the literature, which vary depending on the domain. We reveal the characteristics and limitations of KSD and demonstrate its non-optimality under a certain alternative space, defined over general domains when considering $\chi^2$-divergence as the separation metric. To address this issue of non-optimality, we propose a modified, minimax optimal test by incorporating a spectral regularizer, thereby overcoming the shortcomings of standard KSD tests. Our results are established under a weak moment condition on the Stein kernel, which relaxes the bounded kernel assumption required by prior work in the analysis of kernel-based hypothesis testing. Additionally, we introduce an adaptive test capable of achieving minimax optimality up to a logarithmic factor by adapting to unknown parameters. Through numerical experiments, we illustrate the superior performance of our proposed tests across various domains compared to their unregularized counterparts.

Statistical Optimality and Computational Efficiency of Nyström Kernel PCA

Kernel methods provide an elegant framework for developing nonlinear learning algorithms from simple linear methods. Though these methods have superior empirical performance in several real data applications, their usefulness is inhibited by the significant computational burden incurred in large sample situations. Various approximation schemes have been proposed in the literature to alleviate these computational issues, and the approximate kernel machines are shown to retain the empirical performance. However, the theoretical properties of these approximate kernel machines are less well understood. In this work, we theoretically study the trade-off between computational complexity and statistical accuracy in Nystr\"om approximate kernel principal component analysis (KPCA), wherein we show that the Nystr\"om approximate KPCA matches the statistical performance of (non-approximate) KPCA while remaining computationally beneficial. Additionally, we show that Nystr\"om approximate KPCA outperforms the statistical behavior of another popular approximation scheme, the random feature approximation, when applied to KPCA.

Robust Persistence Diagrams using Reproducing Kernels

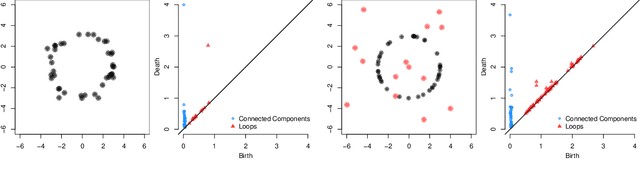
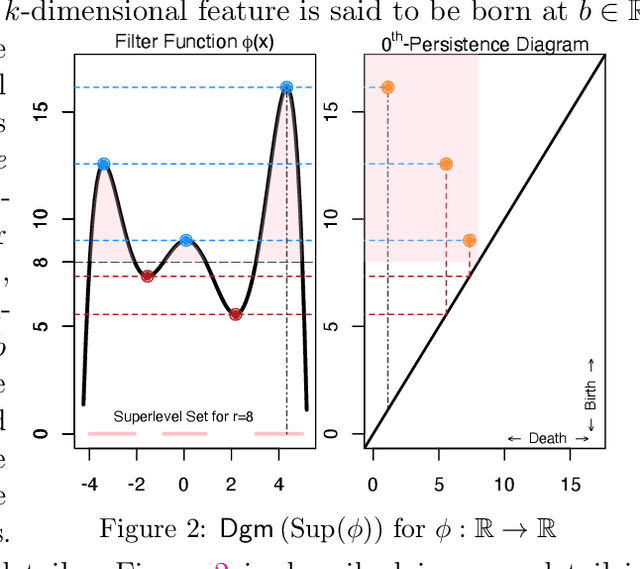
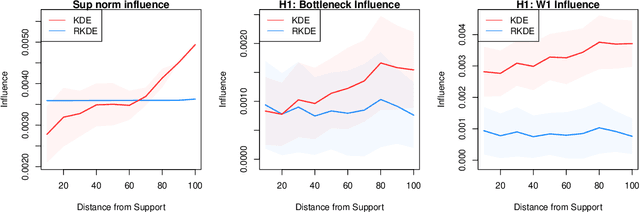
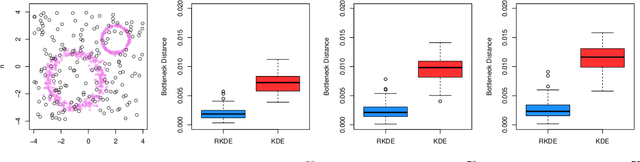
Persistent homology has become an important tool for extracting geometric and topological features from data, whose multi-scale features are summarized in a persistence diagram. From a statistical perspective, however, persistence diagrams are very sensitive to perturbations in the input space. In this work, we develop a framework for constructing robust persistence diagrams from superlevel filtrations of robust density estimators constructed using reproducing kernels. Using an analogue of the influence function on the space of persistence diagrams, we establish the proposed framework to be less sensitive to outliers. The robust persistence diagrams are shown to be consistent estimators in bottleneck distance, with the convergence rate controlled by the smoothness of the kernel. This, in turn, allows us to construct uniform confidence bands in the space of persistence diagrams. Finally, we demonstrate the superiority of the proposed approach on benchmark datasets.

Gain with no Pain: Efficient Kernel-PCA by Nyström Sampling

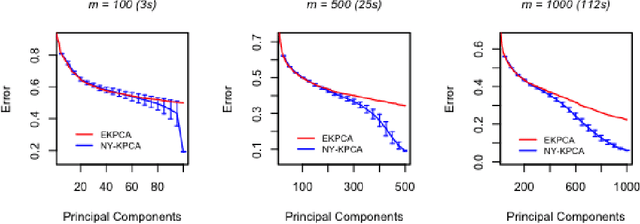
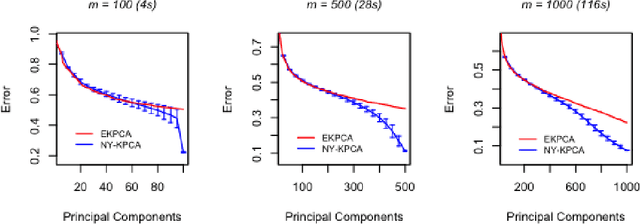
In this paper, we propose and study a Nystr\"om based approach to efficient large scale kernel principal component analysis (PCA). The latter is a natural nonlinear extension of classical PCA based on considering a nonlinear feature map or the corresponding kernel. Like other kernel approaches, kernel PCA enjoys good mathematical and statistical properties but, numerically, it scales poorly with the sample size. Our analysis shows that Nystr\"om sampling greatly improves computational efficiency without incurring any loss of statistical accuracy. While similar effects have been observed in supervised learning, this is the first such result for PCA. Our theoretical findings, which are also illustrated by numerical results, are based on a combination of analytic and concentration of measure techniques. Our study is more broadly motivated by the question of understanding the interplay between statistical and computational requirements for learning.

Approximate Kernel PCA Using Random Features: Computational vs. Statistical Trade-off

Kernel methods are powerful learning methodologies that provide a simple way to construct nonlinear algorithms from linear ones. Despite their popularity, they suffer from poor scalability in big data scenarios. Various approximation methods, including random feature approximation have been proposed to alleviate the problem. However, the statistical consistency of most of these approximate kernel methods is not well understood except for kernel ridge regression wherein it has been shown that the random feature approximation is not only computationally efficient but also statistically consistent with a minimax optimal rate of convergence. In this paper, we investigate the efficacy of random feature approximation in the context of kernel principal component analysis (KPCA) by studying the trade-off between computational and statistical behaviors of approximate KPCA. We show that the approximate KPCA is both computationally and statistically efficient compared to KPCA in terms of the error associated with reconstructing a kernel function based on its projection onto the corresponding eigenspaces. Depending on the eigenvalue decay behavior of the covariance operator, we show that only $n^{2/3}$ features (polynomial decay) or $\sqrt{n}$ features (exponential decay) are needed to match the statistical performance of KPCA. We also investigate their statistical behaviors in terms of the convergence of corresponding eigenspaces wherein we show that only $\sqrt{n}$ features are required to match the performance of KPCA and if fewer than $\sqrt{n}$ features are used, then approximate KPCA has a worse statistical behavior than that of KPCA.

Density Estimation in Infinite Dimensional Exponential Families

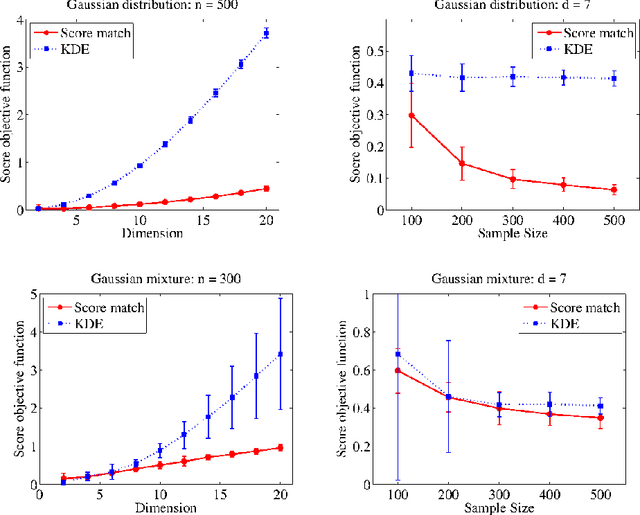
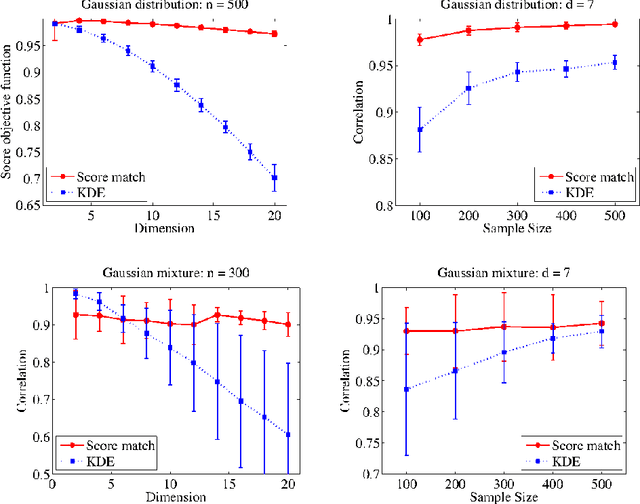
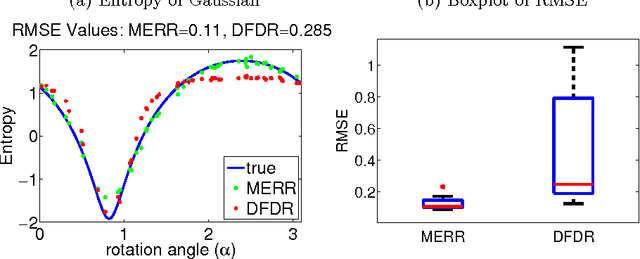
In this paper, we consider an infinite dimensional exponential family, $\mathcal{P}$ of probability densities, which are parametrized by functions in a reproducing kernel Hilbert space, $H$ and show it to be quite rich in the sense that a broad class of densities on $\mathbb{R}^d$ can be approximated arbitrarily well in Kullback-Leibler (KL) divergence by elements in $\mathcal{P}$. The main goal of the paper is to estimate an unknown density, $p_0$ through an element in $\mathcal{P}$. Standard techniques like maximum likelihood estimation (MLE) or pseudo MLE (based on the method of sieves), which are based on minimizing the KL divergence between $p_0$ and $\mathcal{P}$, do not yield practically useful estimators because of their inability to efficiently handle the log-partition function. Instead, we propose an estimator, $\hat{p}_n$ based on minimizing the \emph{Fisher divergence}, $J(p_0\Vert p)$ between $p_0$ and $p\in \mathcal{P}$, which involves solving a simple finite-dimensional linear system. When $p_0\in\mathcal{P}$, we show that the proposed estimator is consistent, and provide a convergence rate of $n^{-\min\left\{\frac{2}{3},\frac{2\beta+1}{2\beta+2}\right\}}$ in Fisher divergence under the smoothness assumption that $\log p_0\in\mathcal{R}(C^\beta)$ for some $\beta\ge 0$, where $C$ is a certain Hilbert-Schmidt operator on $H$ and $\mathcal{R}(C^\beta)$ denotes the image of $C^\beta$. We also investigate the misspecified case of $p_0\notin\mathcal{P}$ and show that $J(p_0\Vert\hat{p}_n)\rightarrow \inf_{p\in\mathcal{P}}J(p_0\Vert p)$ as $n\rightarrow\infty$, and provide a rate for this convergence under a similar smoothness condition as above. Through numerical simulations we demonstrate that the proposed estimator outperforms the non-parametric kernel density estimator, and that the advantage with the proposed estimator grows as $d$ increases.

Kernel Mean Embedding of Distributions: A Review and Beyond

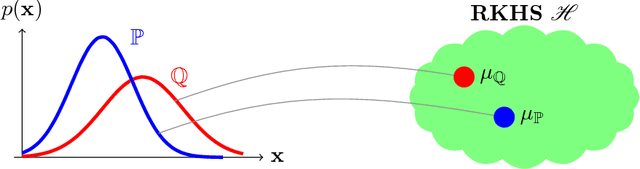
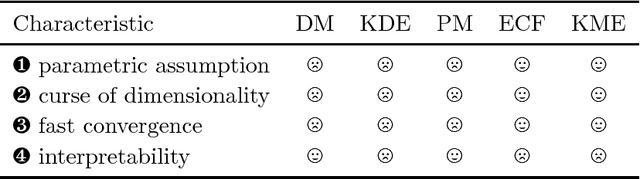
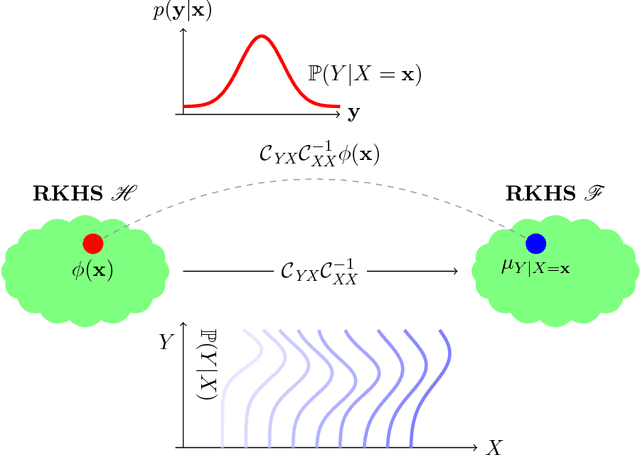
A Hilbert space embedding of a distribution---in short, a kernel mean embedding---has recently emerged as a powerful tool for machine learning and inference. The basic idea behind this framework is to map distributions into a reproducing kernel Hilbert space (RKHS) in which the whole arsenal of kernel methods can be extended to probability measures. It can be viewed as a generalization of the original "feature map" common to support vector machines (SVMs) and other kernel methods. While initially closely associated with the latter, it has meanwhile found application in fields ranging from kernel machines and probabilistic modeling to statistical inference, causal discovery, and deep learning. The goal of this survey is to give a comprehensive review of existing work and recent advances in this research area, and to discuss the most challenging issues and open problems that could lead to new research directions. The survey begins with a brief introduction to the RKHS and positive definite kernels which forms the backbone of this survey, followed by a thorough discussion of the Hilbert space embedding of marginal distributions, theoretical guarantees, and a review of its applications. The embedding of distributions enables us to apply RKHS methods to probability measures which prompts a wide range of applications such as kernel two-sample testing, independent testing, and learning on distributional data. Next, we discuss the Hilbert space embedding for conditional distributions, give theoretical insights, and review some applications. The conditional mean embedding enables us to perform sum, product, and Bayes' rules---which are ubiquitous in graphical model, probabilistic inference, and reinforcement learning---in a non-parametric way. We then discuss relationships between this framework and other related areas. Lastly, we give some suggestions on future research directions.

Learning Theory for Distribution Regression

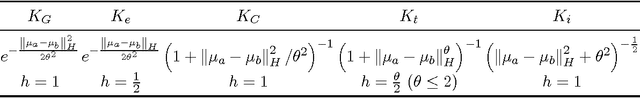
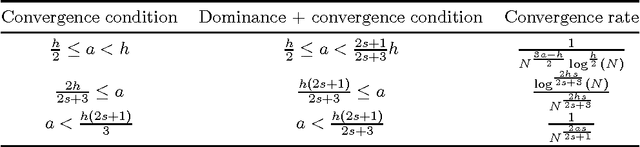
We focus on the distribution regression problem: regressing to vector-valued outputs from probability measures. Many important machine learning and statistical tasks fit into this framework, including multi-instance learning and point estimation problems without analytical solution (such as hyperparameter or entropy estimation). Despite the large number of available heuristics in the literature, the inherent two-stage sampled nature of the problem makes the theoretical analysis quite challenging, since in practice only samples from sampled distributions are observable, and the estimates have to rely on similarities computed between sets of points. To the best of our knowledge, the only existing technique with consistency guarantees for distribution regression requires kernel density estimation as an intermediate step (which often performs poorly in practice), and the domain of the distributions to be compact Euclidean. In this paper, we study a simple, analytically computable, ridge regression-based alternative to distribution regression, where we embed the distributions to a reproducing kernel Hilbert space, and learn the regressor from the embeddings to the outputs. Our main contribution is to prove that this scheme is consistent in the two-stage sampled setup under mild conditions (on separable topological domains enriched with kernels): we present an exact computational-statistical efficiency trade-off analysis showing that our estimator is able to match the one-stage sampled minimax optimal rate [Caponnetto and De Vito, 2007; Steinwart et al., 2009]. This result answers a 17-year-old open question, establishing the consistency of the classical set kernel [Haussler, 1999; Gaertner et. al, 2002] in regression. We also cover consistency for more recent kernels on distributions, including those due to [Christmann and Steinwart, 2010].

Kernel Mean Shrinkage Estimators

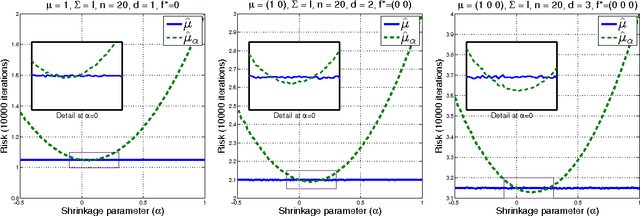
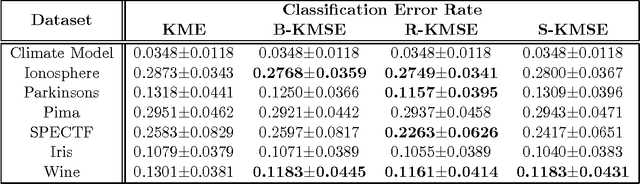
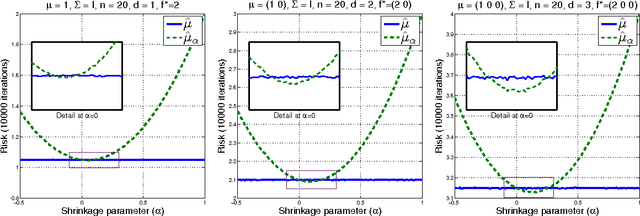
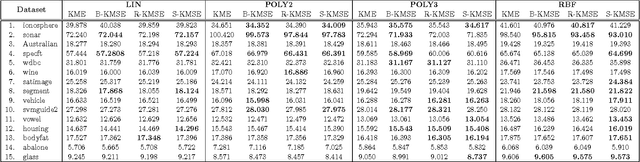
A mean function in a reproducing kernel Hilbert space (RKHS), or a kernel mean, is central to kernel methods in that it is used by many classical algorithms such as kernel principal component analysis, and it also forms the core inference step of modern kernel methods that rely on embedding probability distributions in RKHSs. Given a finite sample, an empirical average has been used commonly as a standard estimator of the true kernel mean. Despite a widespread use of this estimator, we show that it can be improved thanks to the well-known Stein phenomenon. We propose a new family of estimators called kernel mean shrinkage estimators (KMSEs), which benefit from both theoretical justifications and good empirical performance. The results demonstrate that the proposed estimators outperform the standard one, especially in a "large d, small n" paradigm.

Two-stage Sampled Learning Theory on Distributions

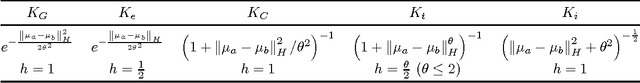
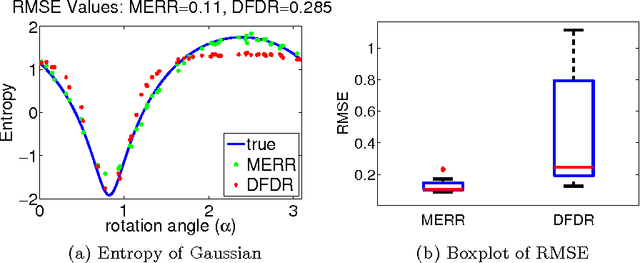
We focus on the distribution regression problem: regressing to a real-valued response from a probability distribution. Although there exist a large number of similarity measures between distributions, very little is known about their generalization performance in specific learning tasks. Learning problems formulated on distributions have an inherent two-stage sampled difficulty: in practice only samples from sampled distributions are observable, and one has to build an estimate on similarities computed between sets of points. To the best of our knowledge, the only existing method with consistency guarantees for distribution regression requires kernel density estimation as an intermediate step (which suffers from slow convergence issues in high dimensions), and the domain of the distributions to be compact Euclidean. In this paper, we provide theoretical guarantees for a remarkably simple algorithmic alternative to solve the distribution regression problem: embed the distributions to a reproducing kernel Hilbert space, and learn a ridge regressor from the embeddings to the outputs. Our main contribution is to prove the consistency of this technique in the two-stage sampled setting under mild conditions (on separable, topological domains endowed with kernels). For a given total number of observations, we derive convergence rates as an explicit function of the problem difficulty. As a special case, we answer a 15-year-old open question: we establish the consistency of the classical set kernel [Haussler, 1999; Gartner et. al, 2002] in regression, and cover more recent kernels on distributions, including those due to [Christmann and Steinwart, 2010].