Statistical Optimality and Computational Efficiency of Nyström Kernel PCA

Kernel methods provide an elegant framework for developing nonlinear learning algorithms from simple linear methods. Though these methods have superior empirical performance in several real data applications, their usefulness is inhibited by the significant computational burden incurred in large sample situations. Various approximation schemes have been proposed in the literature to alleviate these computational issues, and the approximate kernel machines are shown to retain the empirical performance. However, the theoretical properties of these approximate kernel machines are less well understood. In this work, we theoretically study the trade-off between computational complexity and statistical accuracy in Nystr\"om approximate kernel principal component analysis (KPCA), wherein we show that the Nystr\"om approximate KPCA matches the statistical performance of (non-approximate) KPCA while remaining computationally beneficial. Additionally, we show that Nystr\"om approximate KPCA outperforms the statistical behavior of another popular approximation scheme, the random feature approximation, when applied to KPCA.

Gain with no Pain: Efficient Kernel-PCA by Nyström Sampling

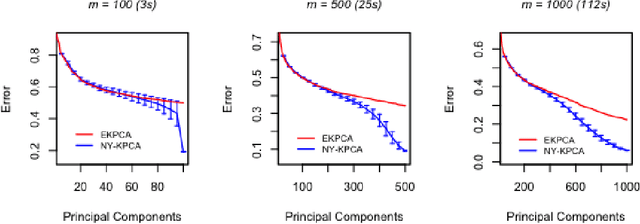
In this paper, we propose and study a Nystr\"om based approach to efficient large scale kernel principal component analysis (PCA). The latter is a natural nonlinear extension of classical PCA based on considering a nonlinear feature map or the corresponding kernel. Like other kernel approaches, kernel PCA enjoys good mathematical and statistical properties but, numerically, it scales poorly with the sample size. Our analysis shows that Nystr\"om sampling greatly improves computational efficiency without incurring any loss of statistical accuracy. While similar effects have been observed in supervised learning, this is the first such result for PCA. Our theoretical findings, which are also illustrated by numerical results, are based on a combination of analytic and concentration of measure techniques. Our study is more broadly motivated by the question of understanding the interplay between statistical and computational requirements for learning.

Approximate Kernel PCA Using Random Features: Computational vs. Statistical Trade-off

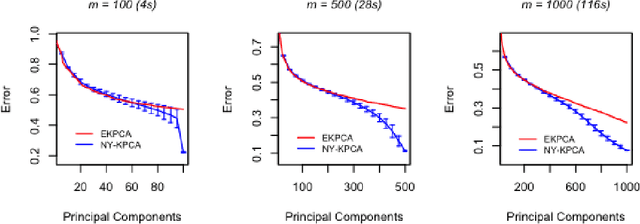
Kernel methods are powerful learning methodologies that provide a simple way to construct nonlinear algorithms from linear ones. Despite their popularity, they suffer from poor scalability in big data scenarios. Various approximation methods, including random feature approximation have been proposed to alleviate the problem. However, the statistical consistency of most of these approximate kernel methods is not well understood except for kernel ridge regression wherein it has been shown that the random feature approximation is not only computationally efficient but also statistically consistent with a minimax optimal rate of convergence. In this paper, we investigate the efficacy of random feature approximation in the context of kernel principal component analysis (KPCA) by studying the trade-off between computational and statistical behaviors of approximate KPCA. We show that the approximate KPCA is both computationally and statistically efficient compared to KPCA in terms of the error associated with reconstructing a kernel function based on its projection onto the corresponding eigenspaces. Depending on the eigenvalue decay behavior of the covariance operator, we show that only $n^{2/3}$ features (polynomial decay) or $\sqrt{n}$ features (exponential decay) are needed to match the statistical performance of KPCA. We also investigate their statistical behaviors in terms of the convergence of corresponding eigenspaces wherein we show that only $\sqrt{n}$ features are required to match the performance of KPCA and if fewer than $\sqrt{n}$ features are used, then approximate KPCA has a worse statistical behavior than that of KPCA.