Gain with no Pain: Efficient Kernel-PCA by Nyström Sampling
Paper and Code
Jul 11, 2019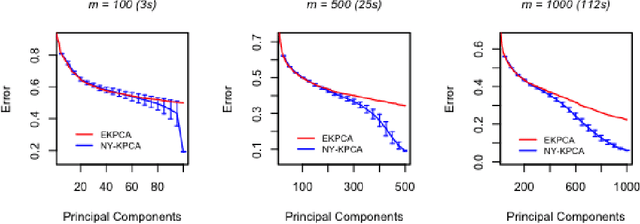
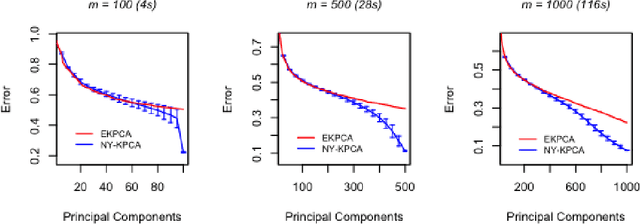
In this paper, we propose and study a Nystr\"om based approach to efficient large scale kernel principal component analysis (PCA). The latter is a natural nonlinear extension of classical PCA based on considering a nonlinear feature map or the corresponding kernel. Like other kernel approaches, kernel PCA enjoys good mathematical and statistical properties but, numerically, it scales poorly with the sample size. Our analysis shows that Nystr\"om sampling greatly improves computational efficiency without incurring any loss of statistical accuracy. While similar effects have been observed in supervised learning, this is the first such result for PCA. Our theoretical findings, which are also illustrated by numerical results, are based on a combination of analytic and concentration of measure techniques. Our study is more broadly motivated by the question of understanding the interplay between statistical and computational requirements for learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge