Gaussian and Bootstrap Approximation for Matching-based Average Treatment Effect Estimators

We establish Gaussian approximation bounds for covariate and rank-matching-based Average Treatment Effect (ATE) estimators. By analyzing these estimators through the lens of stabilization theory, we employ the Malliavin-Stein method to derive our results. Our bounds precisely quantify the impact of key problem parameters, including the number of matches and treatment balance, on the accuracy of the Gaussian approximation. Additionally, we develop multiplier bootstrap procedures to estimate the limiting distribution in a fully data-driven manner, and we leverage the derived Gaussian approximation results to further obtain bootstrap approximation bounds. Our work not only introduces a novel theoretical framework for commonly used ATE estimators, but also provides data-driven methods for constructing non-asymptotically valid confidence intervals.

Provable In-context Learning for Mixture of Linear Regressions using Transformers

We theoretically investigate the in-context learning capabilities of transformers in the context of learning mixtures of linear regression models. For the case of two mixtures, we demonstrate the existence of transformers that can achieve an accuracy, relative to the oracle predictor, of order $\mathcal{\tilde{O}}((d/n)^{1/4})$ in the low signal-to-noise ratio (SNR) regime and $\mathcal{\tilde{O}}(\sqrt{d/n})$ in the high SNR regime, where $n$ is the length of the prompt, and $d$ is the dimension of the problem. Additionally, we derive in-context excess risk bounds of order $\mathcal{O}(L/\sqrt{B})$, where $B$ denotes the number of (training) prompts, and $L$ represents the number of attention layers. The order of $L$ depends on whether the SNR is low or high. In the high SNR regime, we extend the results to $K$-component mixture models for finite $K$. Extensive simulations also highlight the advantages of transformers for this task, outperforming other baselines such as the Expectation-Maximization algorithm.

Transformers Handle Endogeneity in In-Context Linear Regression

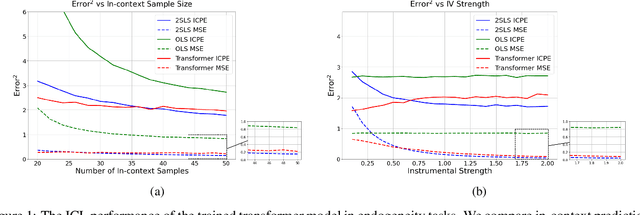
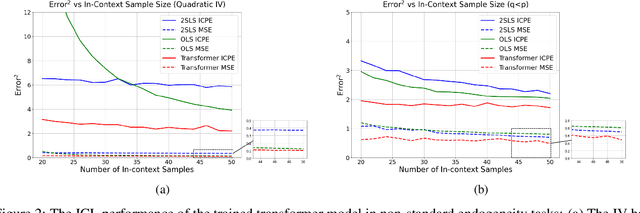
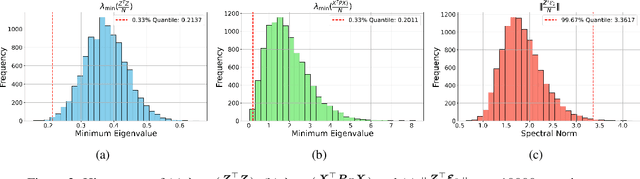
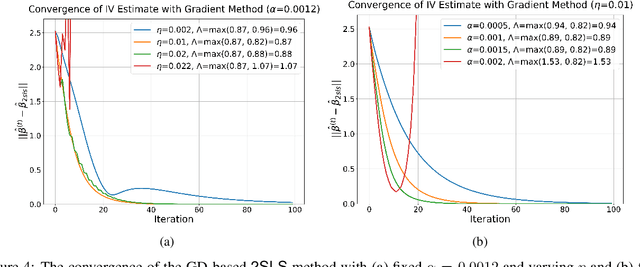
We explore the capability of transformers to address endogeneity in in-context linear regression. Our main finding is that transformers inherently possess a mechanism to handle endogeneity effectively using instrumental variables (IV). First, we demonstrate that the transformer architecture can emulate a gradient-based bi-level optimization procedure that converges to the widely used two-stage least squares $(\textsf{2SLS})$ solution at an exponential rate. Next, we propose an in-context pretraining scheme and provide theoretical guarantees showing that the global minimizer of the pre-training loss achieves a small excess loss. Our extensive experiments validate these theoretical findings, showing that the trained transformer provides more robust and reliable in-context predictions and coefficient estimates than the $\textsf{2SLS}$ method, in the presence of endogeneity.

Improved Finite-Particle Convergence Rates for Stein Variational Gradient Descent

We provide finite-particle convergence rates for the Stein Variational Gradient Descent (SVGD) algorithm in the Kernel Stein Discrepancy ($\mathsf{KSD}$) and Wasserstein-2 metrics. Our key insight is the observation that the time derivative of the relative entropy between the joint density of $N$ particle locations and the $N$-fold product target measure, starting from a regular initial distribution, splits into a dominant `negative part' proportional to $N$ times the expected $\mathsf{KSD}^2$ and a smaller `positive part'. This observation leads to $\mathsf{KSD}$ rates of order $1/\sqrt{N}$, providing a near optimal double exponential improvement over the recent result by~\cite{shi2024finite}. Under mild assumptions on the kernel and potential, these bounds also grow linearly in the dimension $d$. By adding a bilinear component to the kernel, the above approach is used to further obtain Wasserstein-2 convergence. For the case of `bilinear + Mat\'ern' kernels, we derive Wasserstein-2 rates that exhibit a curse-of-dimensionality similar to the i.i.d. setting. We also obtain marginal convergence and long-time propagation of chaos results for the time-averaged particle laws.

Stochastic Optimization Algorithms for Instrumental Variable Regression with Streaming Data

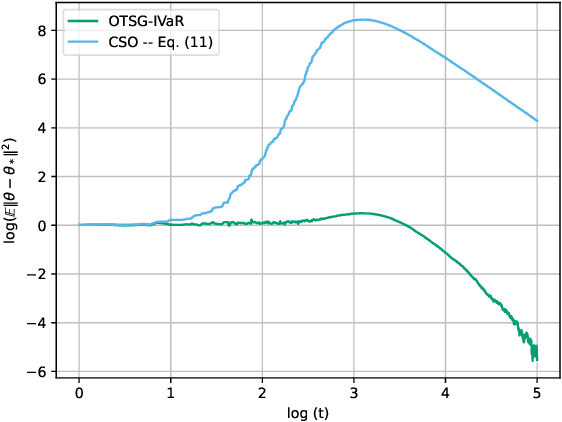
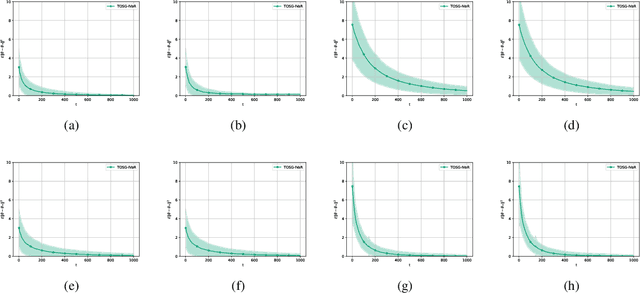
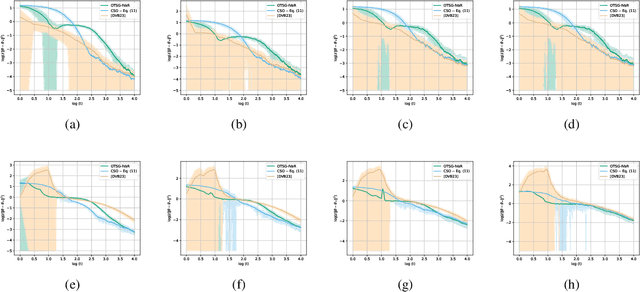
We develop and analyze algorithms for instrumental variable regression by viewing the problem as a conditional stochastic optimization problem. In the context of least-squares instrumental variable regression, our algorithms neither require matrix inversions nor mini-batches and provides a fully online approach for performing instrumental variable regression with streaming data. When the true model is linear, we derive rates of convergence in expectation, that are of order $\mathcal{O}(\log T/T)$ and $\mathcal{O}(1/T^{1-\iota})$ for any $\iota>0$, respectively under the availability of two-sample and one-sample oracles, respectively, where $T$ is the number of iterations. Importantly, under the availability of the two-sample oracle, our procedure avoids explicitly modeling and estimating the relationship between confounder and the instrumental variables, demonstrating the benefit of the proposed approach over recent works based on reformulating the problem as minimax optimization problems. Numerical experiments are provided to corroborate the theoretical results.

A Separation in Heavy-Tailed Sampling: Gaussian vs. Stable Oracles for Proximal Samplers

We study the complexity of heavy-tailed sampling and present a separation result in terms of obtaining high-accuracy versus low-accuracy guarantees i.e., samplers that require only $O(\log(1/\varepsilon))$ versus $\Omega(\text{poly}(1/\varepsilon))$ iterations to output a sample which is $\varepsilon$-close to the target in $\chi^2$-divergence. Our results are presented for proximal samplers that are based on Gaussian versus stable oracles. We show that proximal samplers based on the Gaussian oracle have a fundamental barrier in that they necessarily achieve only low-accuracy guarantees when sampling from a class of heavy-tailed targets. In contrast, proximal samplers based on the stable oracle exhibit high-accuracy guarantees, thereby overcoming the aforementioned limitation. We also prove lower bounds for samplers under the stable oracle and show that our upper bounds cannot be fundamentally improved.

Minimax Optimal Goodness-of-Fit Testing with Kernel Stein Discrepancy

We explore the minimax optimality of goodness-of-fit tests on general domains using the kernelized Stein discrepancy (KSD). The KSD framework offers a flexible approach for goodness-of-fit testing, avoiding strong distributional assumptions, accommodating diverse data structures beyond Euclidean spaces, and relying only on partial knowledge of the reference distribution, while maintaining computational efficiency. We establish a general framework and an operator-theoretic representation of the KSD, encompassing many existing KSD tests in the literature, which vary depending on the domain. We reveal the characteristics and limitations of KSD and demonstrate its non-optimality under a certain alternative space, defined over general domains when considering $\chi^2$-divergence as the separation metric. To address this issue of non-optimality, we propose a modified, minimax optimal test by incorporating a spectral regularizer, thereby overcoming the shortcomings of standard KSD tests. Our results are established under a weak moment condition on the Stein kernel, which relaxes the bounded kernel assumption required by prior work in the analysis of kernel-based hypothesis testing. Additionally, we introduce an adaptive test capable of achieving minimax optimality up to a logarithmic factor by adapting to unknown parameters. Through numerical experiments, we illustrate the superior performance of our proposed tests across various domains compared to their unregularized counterparts.

Meta-Learning with Generalized Ridge Regression: High-dimensional Asymptotics, Optimality and Hyper-covariance Estimation

Meta-learning involves training models on a variety of training tasks in a way that enables them to generalize well on new, unseen test tasks. In this work, we consider meta-learning within the framework of high-dimensional multivariate random-effects linear models and study generalized ridge-regression based predictions. The statistical intuition of using generalized ridge regression in this setting is that the covariance structure of the random regression coefficients could be leveraged to make better predictions on new tasks. Accordingly, we first characterize the precise asymptotic behavior of the predictive risk for a new test task when the data dimension grows proportionally to the number of samples per task. We next show that this predictive risk is optimal when the weight matrix in generalized ridge regression is chosen to be the inverse of the covariance matrix of random coefficients. Finally, we propose and analyze an estimator of the inverse covariance matrix of random regression coefficients based on data from the training tasks. As opposed to intractable MLE-type estimators, the proposed estimators could be computed efficiently as they could be obtained by solving (global) geodesically-convex optimization problems. Our analysis and methodology use tools from random matrix theory and Riemannian optimization. Simulation results demonstrate the improved generalization performance of the proposed method on new unseen test tasks within the considered framework.

Multivariate Gaussian Approximation for Random Forest via Region-based Stabilization

We derive Gaussian approximation bounds for random forest predictions based on a set of training points given by a Poisson process, under fairly mild regularity assumptions on the data generating process. Our approach is based on the key observation that the random forest predictions satisfy a certain geometric property called region-based stabilization. In the process of developing our results for the random forest, we also establish a probabilistic result, which might be of independent interest, on multivariate Gaussian approximation bounds for general functionals of Poisson process that are region-based stabilizing. This general result makes use of the Malliavin-Stein method, and is potentially applicable to various related statistical problems.

Nonsmooth Nonparametric Regression via Fractional Laplacian Eigenmaps

We develop nonparametric regression methods for the case when the true regression function is not necessarily smooth. More specifically, our approach is using the fractional Laplacian and is designed to handle the case when the true regression function lies in an $L_2$-fractional Sobolev space with order $s\in (0,1)$. This function class is a Hilbert space lying between the space of square-integrable functions and the first-order Sobolev space consisting of differentiable functions. It contains fractional power functions, piecewise constant or polynomial functions and bump function as canonical examples. For the proposed approach, we prove upper bounds on the in-sample mean-squared estimation error of order $n^{-\frac{2s}{2s+d}}$, where $d$ is the dimension, $s$ is the aforementioned order parameter and $n$ is the number of observations. We also provide preliminary empirical results validating the practical performance of the developed estimators.