Provable In-context Learning for Mixture of Linear Regressions using Transformers

We theoretically investigate the in-context learning capabilities of transformers in the context of learning mixtures of linear regression models. For the case of two mixtures, we demonstrate the existence of transformers that can achieve an accuracy, relative to the oracle predictor, of order $\mathcal{\tilde{O}}((d/n)^{1/4})$ in the low signal-to-noise ratio (SNR) regime and $\mathcal{\tilde{O}}(\sqrt{d/n})$ in the high SNR regime, where $n$ is the length of the prompt, and $d$ is the dimension of the problem. Additionally, we derive in-context excess risk bounds of order $\mathcal{O}(L/\sqrt{B})$, where $B$ denotes the number of (training) prompts, and $L$ represents the number of attention layers. The order of $L$ depends on whether the SNR is low or high. In the high SNR regime, we extend the results to $K$-component mixture models for finite $K$. Extensive simulations also highlight the advantages of transformers for this task, outperforming other baselines such as the Expectation-Maximization algorithm.

Transformers Handle Endogeneity in In-Context Linear Regression

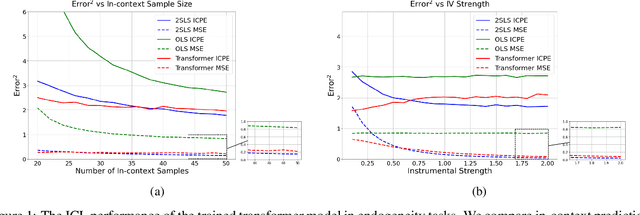
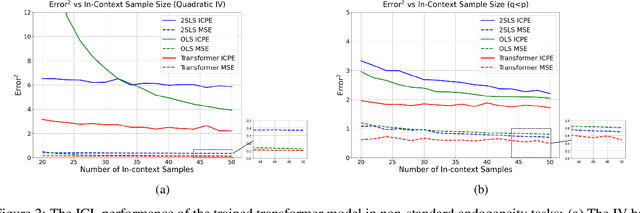
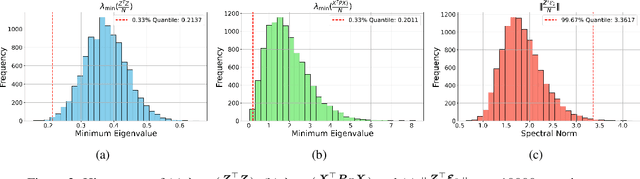
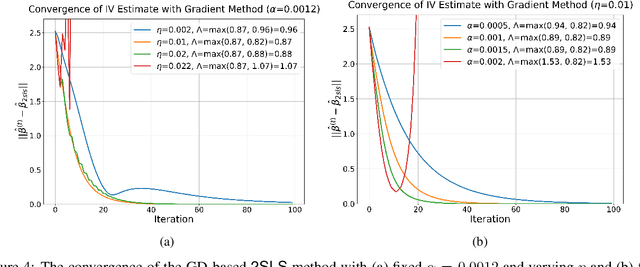
We explore the capability of transformers to address endogeneity in in-context linear regression. Our main finding is that transformers inherently possess a mechanism to handle endogeneity effectively using instrumental variables (IV). First, we demonstrate that the transformer architecture can emulate a gradient-based bi-level optimization procedure that converges to the widely used two-stage least squares $(\textsf{2SLS})$ solution at an exponential rate. Next, we propose an in-context pretraining scheme and provide theoretical guarantees showing that the global minimizer of the pre-training loss achieves a small excess loss. Our extensive experiments validate these theoretical findings, showing that the trained transformer provides more robust and reliable in-context predictions and coefficient estimates than the $\textsf{2SLS}$ method, in the presence of endogeneity.

Distributed Dual Coordinate Ascent with Imbalanced Data on a General Tree Network

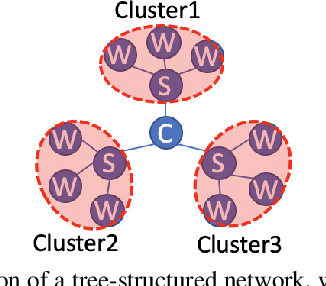
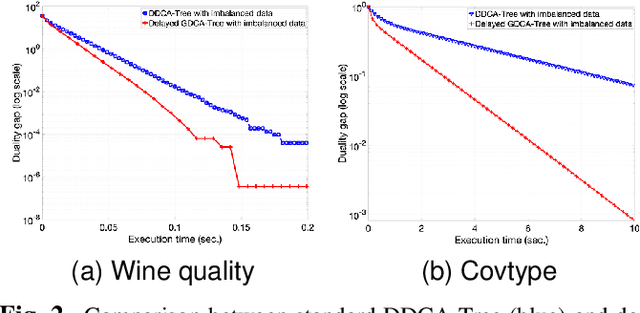
In this paper, we investigate the impact of imbalanced data on the convergence of distributed dual coordinate ascent in a tree network for solving an empirical loss minimization problem in distributed machine learning. To address this issue, we propose a method called delayed generalized distributed dual coordinate ascent that takes into account the information of the imbalanced data, and provide the analysis of the proposed algorithm. Numerical experiments confirm the effectiveness of our proposed method in improving the convergence speed of distributed dual coordinate ascent in a tree network.

Minimax Optimal $Q$ Learning with Nearest Neighbors

$Q$ learning is a popular model free reinforcement learning method. Most of existing works focus on analyzing $Q$ learning for finite state and action spaces. If the state space is continuous, then the original $Q$ learning method can not be directly used. A modification of the original $Q$ learning method was proposed in (Shah and Xie, 2018), which estimates $Q$ values with nearest neighbors. Such modification makes $Q$ learning suitable for continuous state space. (Shah and Xie, 2018) shows that the convergence rate of estimated $Q$ function is $\tilde{O}(T^{-1/(d+3)})$, which is slower than the minimax lower bound $\tilde{\Omega}(T^{-1/(d+2)})$, indicating that this method is not efficient. This paper proposes two new $Q$ learning methods to bridge the gap of convergence rates in (Shah and Xie, 2018), with one of them being offline, while the other is online. Despite that we still use nearest neighbor approach to estimate $Q$ function, the algorithms are crucially different from (Shah and Xie, 2018). In particular, we replace the kernel nearest neighbor in discretized region with a direct nearest neighbor approach. Consequently, our approach significantly improves the convergence rate. Moreover, the time complexity is also significantly improved in high dimensional state spaces. Our analysis shows that both offline and online methods are minimax rate optimal.

Efficient Action Robust Reinforcement Learning with Probabilistic Policy Execution Uncertainty

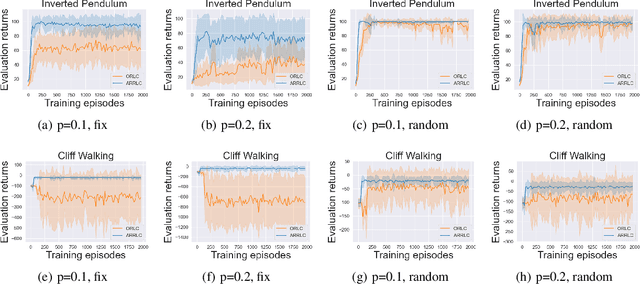
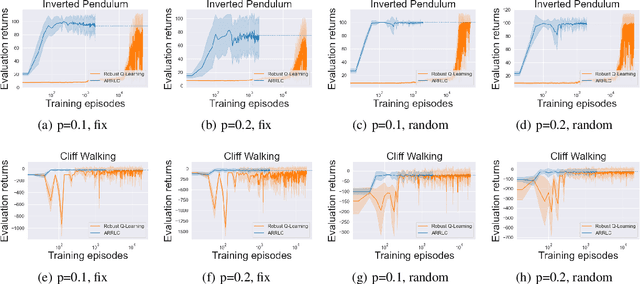
Robust reinforcement learning (RL) aims to find a policy that optimizes the worst-case performance in the face of uncertainties. In this paper, we focus on action robust RL with the probabilistic policy execution uncertainty, in which, instead of always carrying out the action specified by the policy, the agent will take the action specified by the policy with probability $1-\rho$ and an alternative adversarial action with probability $\rho$. We establish the existence of an optimal policy on the action robust MDPs with probabilistic policy execution uncertainty and provide the action robust Bellman optimality equation for its solution. Furthermore, we develop Action Robust Reinforcement Learning with Certificates (ARRLC) algorithm that achieves minimax optimal regret and sample complexity. Furthermore, we conduct numerical experiments to validate our approach's robustness, demonstrating that ARRLC outperforms non-robust RL algorithms and converges faster than the robust TD algorithm in the presence of action perturbations.

Efficient Adversarial Attacks on Online Multi-agent Reinforcement Learning

Due to the broad range of applications of multi-agent reinforcement learning (MARL), understanding the effects of adversarial attacks against MARL model is essential for the safe applications of this model. Motivated by this, we investigate the impact of adversarial attacks on MARL. In the considered setup, there is an exogenous attacker who is able to modify the rewards before the agents receive them or manipulate the actions before the environment receives them. The attacker aims to guide each agent into a target policy or maximize the cumulative rewards under some specific reward function chosen by the attacker, while minimizing the amount of manipulation on feedback and action. We first show the limitations of the action poisoning only attacks and the reward poisoning only attacks. We then introduce a mixed attack strategy with both the action poisoning and the reward poisoning. We show that the mixed attack strategy can efficiently attack MARL agents even if the attacker has no prior information about the underlying environment and the agents' algorithms.

Fairness-aware Regression Robust to Adversarial Attacks

In this paper, we take a first step towards answering the question of how to design fair machine learning algorithms that are robust to adversarial attacks. Using a minimax framework, we aim to design an adversarially robust fair regression model that achieves optimal performance in the presence of an attacker who is able to add a carefully designed adversarial data point to the dataset or perform a rank-one attack on the dataset. By solving the proposed nonsmooth nonconvex-nonconcave minimax problem, the optimal adversary as well as the robust fairness-aware regression model are obtained. For both synthetic data and real-world datasets, numerical results illustrate that the proposed adversarially robust fair models have better performance on poisoned datasets than other fair machine learning models in both prediction accuracy and group-based fairness measure.

Efficiently Escaping Saddle Points in Bilevel Optimization

Bilevel optimization is one of the fundamental problems in machine learning and optimization. Recent theoretical developments in bilevel optimization focus on finding the first-order stationary points for nonconvex-strongly-convex cases. In this paper, we analyze algorithms that can escape saddle points in nonconvex-strongly-convex bilevel optimization. Specifically, we show that the perturbed approximate implicit differentiation (AID) with a warm start strategy finds $\epsilon$-approximate local minimum of bilevel optimization in $\tilde{O}(\epsilon^{-2})$ iterations with high probability. Moreover, we propose an inexact NEgative-curvature-Originated-from-Noise Algorithm (iNEON), a pure first-order algorithm that can escape saddle point and find local minimum of stochastic bilevel optimization. As a by-product, we provide the first nonasymptotic analysis of perturbed multi-step gradient descent ascent (GDmax) algorithm that converges to local minimax point for minimax problems.

Efficient Action Poisoning Attacks on Linear Contextual Bandits

Contextual bandit algorithms have many applicants in a variety of scenarios. In order to develop trustworthy contextual bandit systems, understanding the impacts of various adversarial attacks on contextual bandit algorithms is essential. In this paper, we propose a new class of attacks: action poisoning attacks, where an adversary can change the action signal selected by the agent. We design action poisoning attack schemes against linear contextual bandit algorithms in both white-box and black-box settings. We further analyze the cost of the proposed attack strategies for a very popular and widely used bandit algorithm: LinUCB. We show that, in both white-box and black-box settings, the proposed attack schemes can force the LinUCB agent to pull a target arm very frequently by spending only logarithm cost.

Provably Efficient Black-Box Action Poisoning Attacks Against Reinforcement Learning

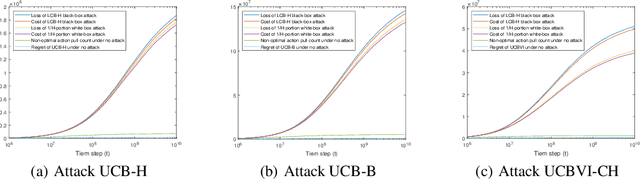
Due to the broad range of applications of reinforcement learning (RL), understanding the effects of adversarial attacks against RL model is essential for the safe applications of this model. Prior theoretical works on adversarial attacks against RL mainly focus on either observation poisoning attacks or environment poisoning attacks. In this paper, we introduce a new class of attacks named action poisoning attacks, where an adversary can change the action signal selected by the agent. Compared with existing attack models, the attacker's ability in the proposed action poisoning attack model is more restricted, which brings some design challenges. We study the action poisoning attack in both white-box and black-box settings. We introduce an adaptive attack scheme called LCB-H, which works for most RL agents in the black-box setting. We prove that the LCB-H attack can force any efficient RL agent, whose dynamic regret scales sublinearly with the total number of steps taken, to choose actions according to a policy selected by the attacker very frequently, with only sublinear cost. In addition, we apply LCB-H attack against a popular model-free RL algorithm: UCB-H. We show that, even in the black-box setting, by spending only logarithm cost, the proposed LCB-H attack scheme can force the UCB-H agent to choose actions according to the policy selected by the attacker very frequently.