Distributed Dual Coordinate Ascent with Imbalanced Data on a General Tree Network

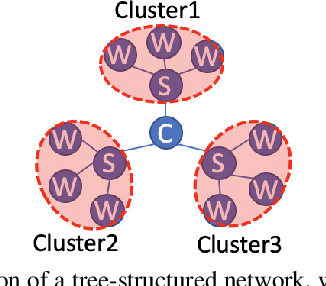
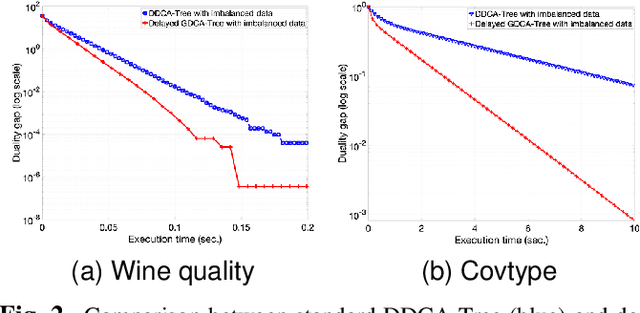
In this paper, we investigate the impact of imbalanced data on the convergence of distributed dual coordinate ascent in a tree network for solving an empirical loss minimization problem in distributed machine learning. To address this issue, we propose a method called delayed generalized distributed dual coordinate ascent that takes into account the information of the imbalanced data, and provide the analysis of the proposed algorithm. Numerical experiments confirm the effectiveness of our proposed method in improving the convergence speed of distributed dual coordinate ascent in a tree network.

Network Constrained Distributed Dual Coordinate Ascent for Machine Learning

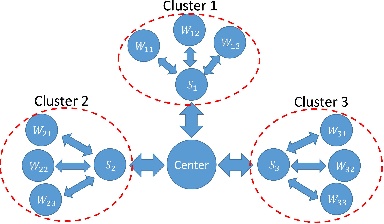
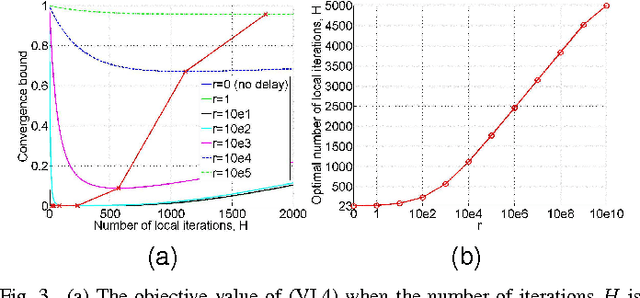
With explosion of data size and limited storage space at a single location, data are often distributed at different locations. We thus face the challenge of performing large-scale machine learning from these distributed data through communication networks. In this paper, we study how the network communication constraints will impact the convergence speed of distributed machine learning optimization algorithms. In particular, we give the convergence rate analysis of the distributed dual coordinate ascent in a general tree structured network. Furthermore, by considering network communication delays, we optimize the network-constrained dual coordinate ascent algorithms to maximize its convergence speed. Our results show that under different network communication delays, to achieve maximum convergence speed, one needs to adopt delay-dependent numbers of local and global iterations for distributed dual coordinate ascent.

Separation-Free Super-Resolution from Compressed Measurements is Possible: an Orthonormal Atomic Norm Minimization Approach

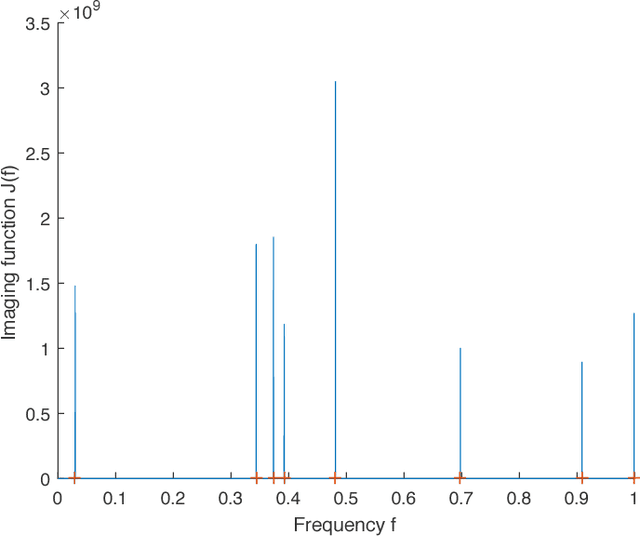
We consider the problem of recovering the superposition of $R$ distinct complex exponential functions from compressed non-uniform time-domain samples. Total Variation (TV) minimization or atomic norm minimization was proposed in the literature to recover the $R$ frequencies or the missing data. However, it is known that in order for TV minimization and atomic norm minimization to recover the missing data or the frequencies, the underlying $R$ frequencies are required to be well-separated, even when the measurements are noiseless. This paper shows that the Hankel matrix recovery approach can super-resolve the $R$ complex exponentials and their frequencies from compressed non-uniform measurements, regardless of how close their frequencies are to each other. We propose a new concept of orthonormal atomic norm minimization (OANM), and demonstrate that the success of Hankel matrix recovery in separation-free super-resolution comes from the fact that the nuclear norm of a Hankel matrix is an orthonormal atomic norm. More specifically, we show that, in traditional atomic norm minimization, the underlying parameter values $\textbf{must}$ be well separated to achieve successful signal recovery, if the atoms are changing continuously with respect to the continuously-valued parameter. In contrast, for the OANM, it is possible the OANM is successful even though the original atoms can be arbitrarily close. As a byproduct of this research, we provide one matrix-theoretic inequality of nuclear norm, and give its proof from the theory of compressed sensing.

Precise Semidefinite Programming Formulation of Atomic Norm Minimization for Recovering d-Dimensional ($d\geq 2$) Off-the-Grid Frequencies

Recent research in off-the-grid compressed sensing (CS) has demonstrated that, under certain conditions, one can successfully recover a spectrally sparse signal from a few time-domain samples even though the dictionary is continuous. In particular, atomic norm minimization was proposed in \cite{tang2012csotg} to recover $1$-dimensional spectrally sparse signal. However, in spite of existing research efforts \cite{chi2013compressive}, it was still an open problem how to formulate an equivalent positive semidefinite program for atomic norm minimization in recovering signals with $d$-dimensional ($d\geq 2$) off-the-grid frequencies. In this paper, we settle this problem by proposing equivalent semidefinite programming formulations of atomic norm minimization to recover signals with $d$-dimensional ($d\geq 2$) off-the-grid frequencies.

Precisely Verifying the Null Space Conditions in Compressed Sensing: A Sandwiching Algorithm

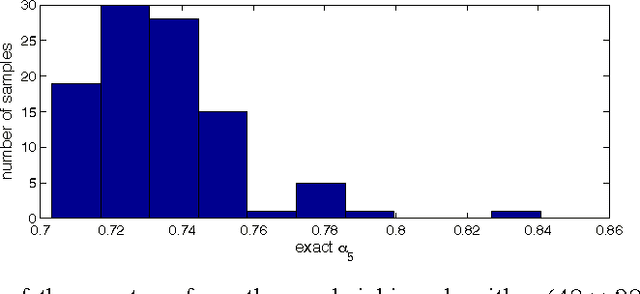
In this paper, we propose new efficient algorithms to verify the null space condition in compressed sensing (CS). Given an $(n-m) \times n$ ($m>0$) CS matrix $A$ and a positive $k$, we are interested in computing $\displaystyle \alpha_k = \max_{\{z: Az=0,z\neq 0\}}\max_{\{K: |K|\leq k\}}$ ${\|z_K \|_{1}}{\|z\|_{1}}$, where $K$ represents subsets of $\{1,2,...,n\}$, and $|K|$ is the cardinality of $K$. In particular, we are interested in finding the maximum $k$ such that $\alpha_k < {1}{2}$. However, computing $\alpha_k$ is known to be extremely challenging. In this paper, we first propose a series of new polynomial-time algorithms to compute upper bounds on $\alpha_k$. Based on these new polynomial-time algorithms, we further design a new sandwiching algorithm, to compute the \emph{exact} $\alpha_k$ with greatly reduced complexity. When needed, this new sandwiching algorithm also achieves a smooth tradeoff between computational complexity and result accuracy. Empirical results show the performance improvements of our algorithm over existing known methods; and our algorithm outputs precise values of $\alpha_k$, with much lower complexity than exhaustive search.

Universally Elevating the Phase Transition Performance of Compressed Sensing: Non-Isometric Matrices are Not Necessarily Bad Matrices

In compressed sensing problems, $\ell_1$ minimization or Basis Pursuit was known to have the best provable phase transition performance of recoverable sparsity among polynomial-time algorithms. It is of great theoretical and practical interest to find alternative polynomial-time algorithms which perform better than $\ell_1$ minimization. \cite{Icassp reweighted l_1}, \cite{Isit reweighted l_1}, \cite{XuScaingLaw} and \cite{iterativereweightedjournal} have shown that a two-stage re-weighted $\ell_1$ minimization algorithm can boost the phase transition performance for signals whose nonzero elements follow an amplitude probability density function (pdf) $f(\cdot)$ whose $t$-th derivative $f^{t}(0) \neq 0$ for some integer $t \geq 0$. However, for signals whose nonzero elements are strictly suspended from zero in distribution (for example, constant-modulus, only taking values `$+d$' or `$-d$' for some nonzero real number $d$), no polynomial-time signal recovery algorithms were known to provide better phase transition performance than plain $\ell_1$ minimization, especially for dense sensing matrices. In this paper, we show that a polynomial-time algorithm can universally elevate the phase-transition performance of compressed sensing, compared with $\ell_1$ minimization, even for signals with constant-modulus nonzero elements. Contrary to conventional wisdoms that compressed sensing matrices are desired to be isometric, we show that non-isometric matrices are not necessarily bad sensing matrices. In this paper, we also provide a framework for recovering sparse signals when sensing matrices are not isometric.