Precisely Verifying the Null Space Conditions in Compressed Sensing: A Sandwiching Algorithm
Paper and Code
Aug 10, 2013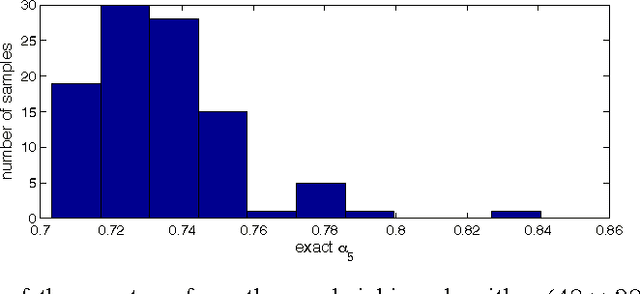



In this paper, we propose new efficient algorithms to verify the null space condition in compressed sensing (CS). Given an $(n-m) \times n$ ($m>0$) CS matrix $A$ and a positive $k$, we are interested in computing $\displaystyle \alpha_k = \max_{\{z: Az=0,z\neq 0\}}\max_{\{K: |K|\leq k\}}$ ${\|z_K \|_{1}}{\|z\|_{1}}$, where $K$ represents subsets of $\{1,2,...,n\}$, and $|K|$ is the cardinality of $K$. In particular, we are interested in finding the maximum $k$ such that $\alpha_k < {1}{2}$. However, computing $\alpha_k$ is known to be extremely challenging. In this paper, we first propose a series of new polynomial-time algorithms to compute upper bounds on $\alpha_k$. Based on these new polynomial-time algorithms, we further design a new sandwiching algorithm, to compute the \emph{exact} $\alpha_k$ with greatly reduced complexity. When needed, this new sandwiching algorithm also achieves a smooth tradeoff between computational complexity and result accuracy. Empirical results show the performance improvements of our algorithm over existing known methods; and our algorithm outputs precise values of $\alpha_k$, with much lower complexity than exhaustive search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge