Dual-View Predictive Diffusion: Lightweight Speech Enhancement via Spectrogram-Image Synergy

Diffusion models have recently set new benchmarks in Speech Enhancement (SE). However, most existing score-based models treat speech spectrograms merely as generic 2D images, applying uniform processing that ignores the intrinsic structural sparsity of audio, which results in inefficient spectral representation and prohibitive computational complexity. To bridge this gap, we propose DVPD, an extremely lightweight Dual-View Predictive Diffusion model, which uniquely exploits the dual nature of spectrograms as both visual textures and physical frequency-domain representations across both training and inference stages. Specifically, during training, we optimize spectral utilization via the Frequency-Adaptive Non-uniform Compression (FANC) encoder, which preserves critical low-frequency harmonics while pruning high-frequency redundancies. Simultaneously, we introduce a Lightweight Image-based Spectro-Awareness (LISA) module to capture features from a visual perspective with minimal overhead. During inference, we propose a Training-free Lossless Boost (TLB) strategy that leverages the same dual-view priors to refine generation quality without any additional fine-tuning. Extensive experiments across various benchmarks demonstrate that DVPD achieves state-of-the-art performance while requiring only 35% of the parameters and 40% of the inference MACs compared to SOTA lightweight model, PGUSE. These results highlight DVPD's superior ability to balance high-fidelity speech quality with extreme architectural efficiency. Code and audio samples are available at the anonymous website: {https://anonymous.4open.science/r/dvpd_demo-E630}

Effective Policy Learning for Multi-Agent Online Coordination Beyond Submodular Objectives

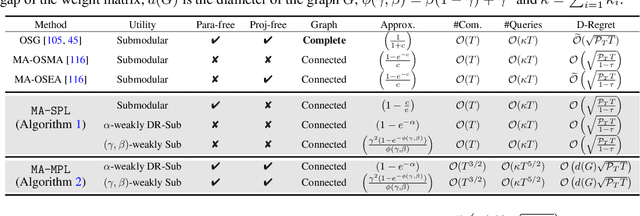
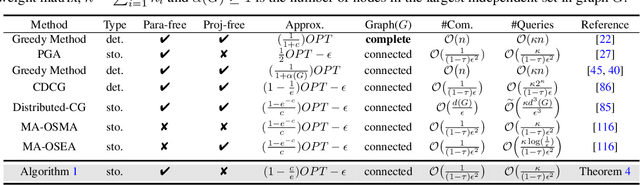
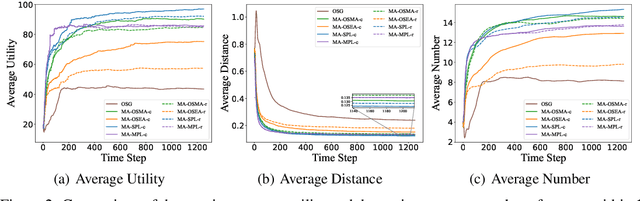
In this paper, we present two effective policy learning algorithms for multi-agent online coordination(MA-OC) problem. The first one, \texttt{MA-SPL}, not only can achieve the optimal $(1-\frac{c}{e})$-approximation guarantee for the MA-OC problem with submodular objectives but also can handle the unexplored $\alpha$-weakly DR-submodular and $(\gamma,\beta)$-weakly submodular scenarios, where $c$ is the curvature of the investigated submodular functions, $\alpha$ denotes the diminishing-return(DR) ratio and the tuple $(\gamma,\beta)$ represents the submodularity ratios. Subsequently, in order to reduce the reliance on the unknown parameters $\alpha,\gamma,\beta$ inherent in the \texttt{MA-SPL} algorithm, we further introduce the second online algorithm named \texttt{MA-MPL}. This \texttt{MA-MPL} algorithm is entirely \emph{parameter-free} and simultaneously can maintain the same approximation ratio as the first \texttt{MA-SPL} algorithm. The core of our \texttt{MA-SPL} and \texttt{MA-MPL} algorithms is a novel continuous-relaxation technique termed as \emph{policy-based continuous extension}. Compared with the well-established \emph{multi-linear extension}, a notable advantage of this new \emph{policy-based continuous extension} is its ability to provide a lossless rounding scheme for any set function, thereby enabling us to tackle the challenging weakly submodular objectives. Finally, extensive simulations are conducted to validate the effectiveness of our proposed algorithms.

On Theoretical Limits of Learning with Label Differential Privacy

Label differential privacy (DP) is designed for learning problems involving private labels and public features. While various methods have been proposed for learning under label DP, the theoretical limits remain largely unexplored. In this paper, we investigate the fundamental limits of learning with label DP in both local and central models for both classification and regression tasks, characterized by minimax convergence rates. We establish lower bounds by converting each task into a multiple hypothesis testing problem and bounding the test error. Additionally, we develop algorithms that yield matching upper bounds. Our results demonstrate that under label local DP (LDP), the risk has a significantly faster convergence rate than that under full LDP, i.e. protecting both features and labels, indicating the advantages of relaxing the DP definition to focus solely on labels. In contrast, under the label central DP (CDP), the risk is only reduced by a constant factor compared to full DP, indicating that the relaxation of CDP only has limited benefits on the performance.

Differential Private Stochastic Optimization with Heavy-tailed Data: Towards Optimal Rates

We study convex optimization problems under differential privacy (DP). With heavy-tailed gradients, existing works achieve suboptimal rates. The main obstacle is that existing gradient estimators have suboptimal tail properties, resulting in a superfluous factor of $d$ in the union bound. In this paper, we explore algorithms achieving optimal rates of DP optimization with heavy-tailed gradients. Our first method is a simple clipping approach. Under bounded $p$-th order moments of gradients, with $n$ samples, it achieves $\tilde{O}(\sqrt{d/n}+\sqrt{d}(\sqrt{d}/n\epsilon)^{1-1/p})$ population risk with $\epsilon\leq 1/\sqrt{d}$. We then propose an iterative updating method, which is more complex but achieves this rate for all $\epsilon\leq 1$. The results significantly improve over existing methods. Such improvement relies on a careful treatment of the tail behavior of gradient estimators. Our results match the minimax lower bound in \cite{kamath2022improved}, indicating that the theoretical limit of stochastic convex optimization under DP is achievable.

Contextual Bandits for Unbounded Context Distributions

Nonparametric contextual bandit is an important model of sequential decision making problems. Under $\alpha$-Tsybakov margin condition, existing research has established a regret bound of $\tilde{O}\left(T^{1-\frac{\alpha+1}{d+2}}\right)$ for bounded supports. However, the optimal regret with unbounded contexts has not been analyzed. The challenge of solving contextual bandit problems with unbounded support is to achieve both exploration-exploitation tradeoff and bias-variance tradeoff simultaneously. In this paper, we solve the nonparametric contextual bandit problem with unbounded contexts. We propose two nearest neighbor methods combined with UCB exploration. The first method uses a fixed $k$. Our analysis shows that this method achieves minimax optimal regret under a weak margin condition and relatively light-tailed context distributions. The second method uses adaptive $k$. By a proper data-driven selection of $k$, this method achieves an expected regret of $\tilde{O}\left(T^{1-\frac{(\alpha+1)\beta}{\alpha+(d+2)\beta}}+T^{1-\beta}\right)$, in which $\beta$ is a parameter describing the tail strength. This bound matches the minimax lower bound up to logarithm factors, indicating that the second method is approximately optimal.

Sequential Federated Learning in Hierarchical Architecture on Non-IID Datasets

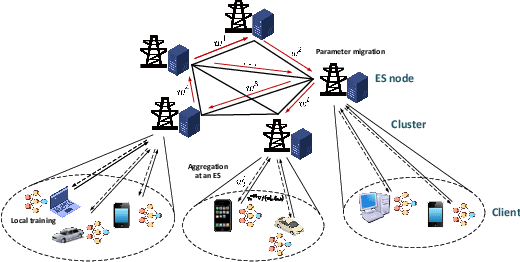
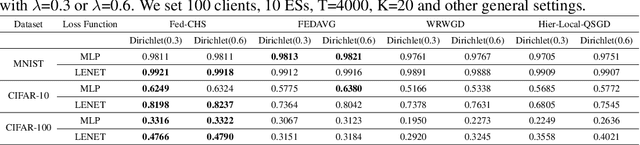
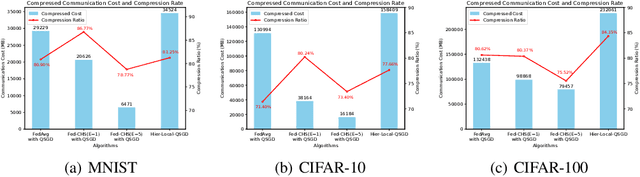
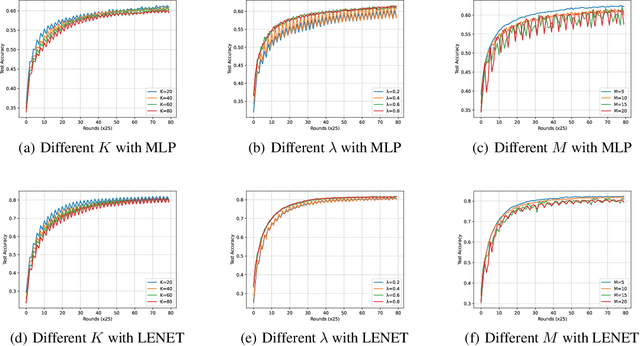
In a real federated learning (FL) system, communication overhead for passing model parameters between the clients and the parameter server (PS) is often a bottleneck. Hierarchical federated learning (HFL) that poses multiple edge servers (ESs) between clients and the PS can partially alleviate communication pressure but still needs the aggregation of model parameters from multiple ESs at the PS. To further reduce communication overhead, we bring sequential FL (SFL) into HFL for the first time, which removes the central PS and enables the model training to be completed only through passing the global model between two adjacent ESs for each iteration, and propose a novel algorithm adaptive to such a combinational framework, referred to as Fed-CHS. Convergence results are derived for strongly convex and non-convex loss functions under various data heterogeneity setups, which show comparable convergence performance with the algorithms for HFL or SFL solely. Experimental results provide evidence of the superiority of our proposed Fed-CHS on both communication overhead saving and test accuracy over baseline methods.

Byzantine-resilient Federated Learning Employing Normalized Gradients on Non-IID Datasets

In practical federated learning (FL) systems, the presence of malicious Byzantine attacks and data heterogeneity often introduces biases into the learning process. However, existing Byzantine-robust methods typically only achieve a compromise between adaptability to different loss function types (including both strongly convex and non-convex) and robustness to heterogeneous datasets, but with non-zero optimality gap. Moreover, this compromise often comes at the cost of high computational complexity for aggregation, which significantly slows down the training speed. To address this challenge, we propose a federated learning approach called Federated Normalized Gradients Algorithm (Fed-NGA). Fed-NGA simply normalizes the uploaded local gradients to be unit vectors before aggregation, achieving a time complexity of $\mathcal{O}(pM)$, where $p$ represents the dimension of model parameters and $M$ is the number of participating clients. This complexity scale achieves the best level among all the existing Byzantine-robust methods. Furthermore, through rigorous proof, we demonstrate that Fed-NGA transcends the trade-off between adaptability to loss function type and data heterogeneity and the limitation of non-zero optimality gap in existing literature. Specifically, Fed-NGA can adapt to both non-convex loss functions and non-IID datasets simultaneously, with zero optimality gap at a rate of $\mathcal{O} (1/T^{\frac{1}{2} - \delta})$, where T is the iteration number and $\delta \in (0,\frac{1}{2})$. In cases where the loss function is strongly convex, the zero optimality gap achieving rate can be improved to be linear. Experimental results provide evidence of the superiority of our proposed Fed-NGA on time complexity and convergence performance over baseline methods.

Learning with User-Level Local Differential Privacy

User-level privacy is important in distributed systems. Previous research primarily focuses on the central model, while the local models have received much less attention. Under the central model, user-level DP is strictly stronger than the item-level one. However, under the local model, the relationship between user-level and item-level LDP becomes more complex, thus the analysis is crucially different. In this paper, we first analyze the mean estimation problem and then apply it to stochastic optimization, classification, and regression. In particular, we propose adaptive strategies to achieve optimal performance at all privacy levels. Moreover, we also obtain information-theoretic lower bounds, which show that the proposed methods are minimax optimal up to logarithmic factors. Unlike the central DP model, where user-level DP always leads to slower convergence, our result shows that under the local model, the convergence rates are nearly the same between user-level and item-level cases for distributions with bounded support. For heavy-tailed distributions, the user-level rate is even faster than the item-level one.

Enhancing Learning with Label Differential Privacy by Vector Approximation

Label differential privacy (DP) is a framework that protects the privacy of labels in training datasets, while the feature vectors are public. Existing approaches protect the privacy of labels by flipping them randomly, and then train a model to make the output approximate the privatized label. However, as the number of classes $K$ increases, stronger randomization is needed, thus the performances of these methods become significantly worse. In this paper, we propose a vector approximation approach, which is easy to implement and introduces little additional computational overhead. Instead of flipping each label into a single scalar, our method converts each label into a random vector with $K$ components, whose expectations reflect class conditional probabilities. Intuitively, vector approximation retains more information than scalar labels. A brief theoretical analysis shows that the performance of our method only decays slightly with $K$. Finally, we conduct experiments on both synthesized and real datasets, which validate our theoretical analysis as well as the practical performance of our method.

CG-FedLLM: How to Compress Gradients in Federated Fune-tuning for Large Language Models

The success of current Large-Language Models (LLMs) hinges on extensive training data that is collected and stored centrally, called Centralized Learning (CL). However, such a collection manner poses a privacy threat, and one potential solution is Federated Learning (FL), which transfers gradients, not raw data, among clients. Unlike traditional networks, FL for LLMs incurs significant communication costs due to their tremendous parameters. This study introduces an innovative approach to compress gradients to improve communication efficiency during LLM FL, formulating the new FL pipeline named CG-FedLLM. This approach integrates an encoder on the client side to acquire the compressed gradient features and a decoder on the server side to reconstruct the gradients. We also developed a novel training strategy that comprises Temporal-ensemble Gradient-Aware Pre-training (TGAP) to identify characteristic gradients of the target model and Federated AutoEncoder-Involved Fine-tuning (FAF) to compress gradients adaptively. Extensive experiments confirm that our approach reduces communication costs and improves performance (e.g., average 3 points increment compared with traditional CL- and FL-based fine-tuning with LlaMA on a well-recognized benchmark, C-Eval). This improvement is because our encoder-decoder, trained via TGAP and FAF, can filter gradients while selectively preserving critical features. Furthermore, we present a series of experimental analyses focusing on the signal-to-noise ratio, compression rate, and robustness within this privacy-centric framework, providing insight into developing more efficient and secure LLMs.